基于融合先验信息的仿真交互可信度评估方法
王玉龙, 董志明, 彭文成, 王晓方
(1. 陆军装甲兵学院演训中心, 北京 100072; 2. 武警后勤学院装备保障系, 天津 300309)
可信度是分布式LVC (Live Virtual and Constructive)仿真系统的关键问题之一。交互事件是分布式LVC仿真系统中系统运行、推进的重要基础,交互行为与事件可信对于系统的可靠运行、仿真的正确计算以及局势的理解与判断至关重要。基于LVC的分布式训练仿真环境,可为参训官兵提供贴近实战的氛围和感受。在实时性要求较高的大规模分布式LVC训练仿真环境中,随着实体数量的不断增加、交互规模的不断扩大,加之广域网的随机网络延迟,会对时间管理服务带来极大的运行负担,可导致中间件开销过高、消息序维护效率低下等问题,无法满足训练仿真活动的实时性和可信性需求。为确保每次仿真推进实体状态的一致性,若采取保守机制,会导致仿真时间严重滞后,且在交互众多、时延复杂的情况下较难获取合理的Lookahead值;若采用乐观机制,则会导致频繁的回滚、中断或容错操作,特别是,在陆战炮击和空战等场景中,会严重破坏演习的连续性和沉浸感,无法保证实兵实装的LVC训练仿真活动能够按照真实演习的节奏、以贴近实战的状态开展。因此,为获得高度可靠的实时LVC仿真能力,在采用独立时间推进机制的同时,可进行系统交互可信状态实时监控,为预先故障管理或容错提供预警机制,以确保实兵实装的LVC训练仿真能够连续、可信地进行。
对于仿真可信度评估问题,MEHTA等[1]指出决策者需要首先明确所使用仿真系统的可信度,才能够基于该系统的仿真结果做出合理决策,不确定性的传播和量化问题、参考数据或间接证据以及仿真校验等是建立仿真可信度的基础;王斐等[2]首先将可信度指标权重确定方法分为主观和客观2类,通过云模型确定主观权重,采用熵权法和信息熵确定客观权重,然后运用加法集成原理获得综合权重,最后使用变权灰色聚类理论获得评价聚类结果,进而分析制导仿真系统的可信度;TANG等[3]针对作战仿真系统的特点,提出了一种基于主题专家知识的主观综合评估方法,并将其应用于作战仿真中,该方法充分利用了主题专家的知识、经验,对评估对象相关因素进行评判,并综合运用层次分析法、模糊综合评判法、模糊层次分析法等对作战仿真系统进行评估,获得整个作战仿真的可信度;潘云龙等[4]提出了基于证据理论和灰云聚类的可信度评估模型,解决了复杂制导仿真系统可信度量化的主观性和不确定性问题,该方法主要采用群组层次分析法获得专家意见并进行证据理论融合,得到高可信度的指标权重,采用灰云聚类方法量化处理定性指标,并计算灰色聚类系数获得仿真系统可信度评估结果。
总体来看,现有文献并未从仿真交互层面考虑系统可信性问题,笔者首先针对分布式LVC训练仿真系统的仿真交互事件,给出了交互可信度的明确定义,根据历史信息和专家经验等先验信息,在引入继承因子的基础上,综合得到交互可信度融合先验分布;然后结合测试环境中交互事件时序和间距等可信度度相关数据,依据交互可信度模型和阈值进行交互可信判断;最后运用贝叶斯方法得到交互可信度的后验分布和实时判断,进而为系统容错或预先故障管理等机制提供实时状态数据支持。该过程是一个实时迭代和更新的过程,在首次后验评估完成后,可使用其后验评估数据和结果对先验信息进行融合与更新,并在此基础上进行新一轮的交互可信度贝叶斯评估,从而获得实时连续的系统交互可信度评估结果,实现对大规模分布式LVC训练仿真系统运行质量的实时在线监控。
1 交互可信度
1.1 交互一致
在分布式LVC仿真系统中,不同的节点都有其认知空间,该认知空间由节点对于实体状态及其交互行为的认知所构成。节点的认知空间不仅包含其自身所维护的实体状态信息,还包括该节点所感知的局部或整个系统的状态及交互信息。在仿真推进过程中,由于存在时钟不同步、时延和信息丢失等问题,节点难以同步、及时有效地获取所需实体状态信息,会导致不同节点对于同一实体的状态和交互行为的认知存在差异,这种认知差异就是分布式LVC训练仿真系统中的交互一致性问题,如图1所示。在大规模分布式LVC训练仿真系统中,随着仿真实体数量的增加,中间件开销不断加大,加之通信网络的局部时延存在差异,不同仿真实体对于其认知空间内状态信息、交互行为和仿真态势的理解存在不一致现象,这在一定程度上损害了仿真的真实性和公平性[5-6]。

图1 LVC训练仿真系统中的交互不一致性
1.2 交互可信判断
在分布式LVC训练仿真系统开发过程中,为了提高开发效率、降低开发成本,允许不同的仿真节点根据模型特点,运用不同的时空描述方法;同时,为丰富和拓展分布式LVC训练仿真系统的应用场景和使用范围,也要求分布式LVC仿真系统可兼容不同开发者和不同建模方法所构建的异构模型资源,这就为实现仿真模型交互的一致性带来了困难。在同一仿真环境或空间中,节点间的信息交互要求不同实体对于同一事件实现一致性的认知与理解。若无法满足交互一致性要求,则可能会给不同用户造成认知差异、困惑与矛盾,甚至会影响仿真结果的正确性,导致用户利益分配不公和仿真失败等严重后果。因此,为保证系统仿真交互的真实性和公平性,应对节点交互的一致性情况进行分析和判断。若交互行为的一致程度满足计算精度、系统规范或用户体验要求,则认为该交互可信;若交互行为的不一致程度较为严重,甚至对分布式LVC训练仿真系统产生违背期望、因果颠倒和理解歧义等不良影响[7],则从用户体验角度来判断,即可认定该仿真交互行为是不可信的。需要明确的是,交互可信只关注仿真事件本身的时序、间距或因果关系是否满足系统要求等问题,而不关注实体模型层面的具体计算结果或概率。图2为在某次炮击事件训练仿真中的交互不可信事件。可以看出:交互可信关注的是射击实体的炮击行为,在某个时间区间内是否都被订阅该信息的不同观察实体观测到,若是,则可初步认定该交互事件可信;否则,认为该交互行为不一致,该事件不可信。至于该炮击行为能否击中目标或击中目标的概率,不在交互可信考虑的范围之内。

图2 某次炮击事件训练仿真中的交互不可信事件
1.3 交互可信模型
交互可信的持续观测需要量化、可测的交互可信度判断模型来支撑。在分布式LVC训练仿真系统中,可采用顺序一致、因果一致等方法维护不同节点的交互一致性,笔者在文献[8]提出的间距一致性模型的基础上,对一致性要求进行重新定义,得到交互可信判断依据。
设V={v1,v2,…,vn},为仿真节点集合,O为所有交互事件的集合,g(om)为事件om的生成节点,R(om)为接收该事件的节点集合,tei为某一事件在节点vi(i=1,2,…,n)上被执行的时间,tei(om)为事件Om在节点vi上被执行的时间。
对于∀om,on∈O,vi,vj∈R(om)∩R(on),j=1,2,…,n,定义
1) 时序一致
tei(om)≤tei(on)⟹tej(om)≤tej(on);
(1)
2) 绝对间距一致
tei(om)-tei(on)=tej(om)-tej(on)。
(2)
考虑到仿真系统及网络环境变化具有很强的随机性,式(2)所要求的绝对间距一致性条件相对苛刻,在分布式LVC训练仿真系统中难以完全满足,为此,笔者重新定义间距一致性要求如下:
|(ts(om)-ts(on))-(tei(om)-tei(on))|≤ε。
(3)
式中:ts(om)为事件om在生成节点g(om)上被发送的时间;ε为间距一致性阈值。
ε主要用来评价同一事件在不同节点满足间距一致要求的程度,并以此为基础判断该交互事件是否可信。若某次交互同时满足时序一致性要求(1)和间距一致性要求(3),则认为该交互可信;反之,则认为该交互不可信。合理的阈值大小对于交互可信评估的有效性至关重要。间距一致性阈值设置不宜过大或过小,过大无法满足间距一致性要求,过小则判断条件过于苛刻,影响系统性能的发挥。
ε的设置可采用k-means聚类方法来实现:首先,在仿真系统运行状态良好的情况下,周期性采集交互事件间距样本,计算每一周期内同一交互事件任意2个节点间距样本的Euclidean距离,得到阈值集合;其次,根据Euclidean距离的大小,采用k-means聚类方法将阈值集合分为2类(Euclidean距离较大的称为交互不可信阈值集,Euclidean距离较小的称为交互可信阈值集);最后,取交互可信阈值集最大者为间距一致性阈值。具体算法流程如下:
输入:若干仿真步长内交互事件的间距数值集合A。
输出:ε。
1) 计算间距数值集合A中每个步长同一交互事件的任意2个节点间距数值的Euclidean距离;
2) 保存Euclidean距离数据集B;
3) 从数据集B中随机选取2个对象作为初始聚类中心;
4) 计算每个对象到聚类中心的距离,并将其重新划分到最近的类中;
5) 计算新类中所有对象的均值,获得2个新的聚类中心;
6) 重复执行步骤4)和5),直到满足最大迭代次数或聚类中心不再大范围移动为止;
7) 保存k-means聚类方法生成的2个聚类集合B1和B2;
8) 根据Euclidean距离大小,将2个聚类分为交互可信阈值集B1和交互不可信阈值集B2;
9) 取交互可信阈值集B1中的最大值为ε赋值。
1.4 交互可信度定义
在量化可测的仿真交互可信判断的基础上,交互可信度为在某一时间区间内,在特定的网络环境下,同时满足时序一致性要求(1)和间距一致性要求(3)的交互事件数量占分布式LVC训练仿真系统总的交互事件的百分比。
2 融合先验分布
2.1 交互可信度先验分布
由于分布式LVC训练仿真系统的运行负载和网络环境时刻处于变化状态,仿真交互事件是否可信是一个随机事件,则交互可信度为一个随机变量。笔者选用β分布作为交互可信度评估的先验分布。记交互可信度为θ,根据分布式LVC训练仿真系统运行历史信息和专家经验,二者的交互可信度先验分布为
(4)

(5)
式中:0≤θ≤1;i=1,为历史信息先验,i=2,为专家经验先验;ai>0、bi>0,为多种信息条件下先验分布的超参数,在先验分布形式已知的情况下,ai、bi的取值是确定先验分布的关键。
2.2 基于历史信息的先验分布
基于历史信息的先验分布主要根据历史数据分析、求解仿真交互可信度均值μ和方差S2,并确定先验分布的超参数
(6)
(7)
2.3 基于专家经验的先验分布
由于专家经验具有模糊性,交互可信度专家经验值通常以连续区间的形式给出。设在某一分布式LVC训练仿真系统的测试阶段,专家经验估计值为θ[θL,θH]。专家估计在区间值[θL,θH]内每一个值的置信度相同,可认为交互可信度θ在区间[θL,θH]上服从均匀分布,并记为θ~U(θL,θH),则均值μ和方差S2分别为
(8)
以先验参数为变量,均值为约束,方差为目标,建立优化模型
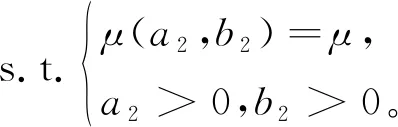
(9)
式中:
分别为β(ai,bi)分布的均值和方差。
利用最优化方法求解式(9)与均匀分布θ~U(θL,θH)拟合程度最高的β分布,即求解β(a2,b2)中的超参数a2、b2,得到交互可信度的专家经验先验分布。
2.4 先验分布融合
为了有效利用先验信息,全面描述先验信息与样本的异总体性,构造融合先验分布
(10)

3 贝叶斯评估
若在分布式LVC训练仿真系统中进行n次独立的交互可信数据采集和判断,其中交互可信的次数为X,则X服从二项分布b(n,θ),交互可信度θ的似然函数为
(11)
根据贝叶斯定理,交互可信度后验分布为
(12)
选后验期望作为θ的贝叶斯评估结论,则交互可信度θ的贝叶斯估计为
(13)
4 仿真实验
为验证交互可信度评估方法的可行性,在一个由20个节点组成的局域网中搭建仿真实验环境,该实验以某训练仿真系统为实验平台,部署RTX实时操作系统,通过调用“RtGetClockTime”函数获取CLOCK_2高精度时钟来实现计时,该时钟精度单位为100 ns,运行环境如图3所示。

图3 训练仿真系统运行环境
交互可信度实验主要分为2部分:
1) 理想环境实验,该实验硬件配置包括2台仿真计算机和1台千兆交换机。2台仿真计算机安装训练仿真基础环境和其他所需软件环境,并分别运行事件发送和接收程序,通过验证收发数据包的一致性,计算测试时长和间距一致性是否满足要求来进行交互可信判断,获得理想环境中交互可信度取值范围,为基于专家经验的先验评估提供参考。
2) 局域网模拟实验,该实验环境为20个节点和1台千兆交换机组成的局域网络环境。每个节点同样部署训练仿真基础环境及其配套软件,为模拟分布式LVC训练仿真系统网络通信高延迟和动态性的特点,使用广域网延迟模拟工具DS2来模拟网络延迟情况。根据其拓展延迟模型,取若干节点作为仿真节点[11],进而构造间距一致性判断模型,并对测试数据进行间距一致性判断;取实验前期若干步长测试结果作为历史先验信息;后续实验结果作为实时测试样本,为贝叶斯后验评估提供数据支持。
典型交互可信度模拟实验测试结果如图4所示。可以看出:
1) 当仿真时间步长在0~20内,训练仿真实验环境交互可信度维持在0.80以上,该系统运行负载稳定,网络环境可靠;

图4 典型交互可信度模拟实验测试结果
2) 当仿真时间步长为25时,交互可信度出现明显下降,其原因可能是广域网随机延迟增大或者训练仿真系统负载增大导致。此时,若交互可信度能及时回升且未对关键交互事件造成误判或仿真运行造成重大结果,短时的系统交互可信度下降可视情忽略;但如果交互可信度急剧或持续下降,则应及时发出预先警告并触发应对措施。
由此可见:交互可信度评估可为训练仿真系统提供关于其运行状态的实时监测和评估结果,进而为及时启动有效的干预措施提供重要判断依据。
5 结论
笔者针对分布式LVC训练仿真系统交互可信度问题,提出了交互可信度的明确定义,建立了交互可信判断模型,量化分析了分布式LVC训练仿真系统交互事件的可信性问题;引入继承因子,对先验信息与样本信息的异总体性进行了判断,融合多种先验信息进行交互可信度的先验分布拟合,提高交互可信度评估的可靠度,并在此基础上运用贝叶斯方法得到了实时连续的交互可信度后验估计。实验结果表明:该方法对于相关变量内涵定义明确,计算简单有效,为分布式LVC训练仿真系统可信度评估问题提供了一种新的思路和方法。
本研究在一定程度上实现了分布式LVC训练仿真系统交互可信度实时状态监控,但对于交互可信度变化的具体原因以及相应的容错方法和措施,并未涉及和分析,有待于下一步进行深入研究和探索。

