变桨风力机非线性扩张状态观测器PID控制

任海军， 侯 斌， 萧 红

(重庆邮电大学 先进制造工程学院,重庆 400065)

0 引 言

风能是一种清洁、无污染以及可再生的绿色能源，风力发电机能把风能转换成电能供人们使用。目前风电系统控制技术使用最多的是变桨距控制，而变桨距控制技术的研究使用最多的控制器是比例-积分-微分(PID)控制器[1]。由于风电系统是一个综合了多种特性的复杂非线性系统，以及风速的不确定性，常规PID控制器难以克服这些困难达到最优控制效果。因此，需要设计更有效的变桨距控制器。

变桨距风力机是在定桨距风力机的基础上加入了主动控制技术[2]，采用变桨距技术控制风电系统，将风力机各部件的受力情况进一步改善，有利于提高大型风力发电机的总体设计和发电质量。在高风速区，通过调节桨距角来限制对风能的吸收，从而保证输出功率维持在额定功率附近。但是由于风力发电环境和风力机自身特性等原因，风电系统很难保证稳定、安全的发电。针对这一问题，近年来学者们进行了很多关于变桨距控制策略的研究[3-7]。

本文提出一种非线性扩张状态观测器PID的变桨风力机输出功率控制策略[8-12]。非线性扩张状态观测器主要作用是测量系统中的未知干扰以及未建模部分，将系统扰动量转换成新的状态变量，同时将观测器的输出信号快速反馈到输入端进行实时补偿，使观测信号与输入端状态变量的估计误差逐渐逼近于零。输入端采用转速偏差和功率偏差作为双闭环控制的两个输入[13-15]，使用PID控制器进行控制。变桨部分设计一个非线性扩张状态观测器，用于测量桨距角和转速的干扰信号，并把观测器输出信号反馈到输入端进行实时补偿。通过Matlab/Simulink仿真实验，表明本文设计的变桨距控制器具有很好的动态特性和鲁棒性。将Matlab/Simulink仿真工具与理论分析相结合，改变控制参数，可以使学生观察到系统状态变量的变化过程，而且，这种以图形直观表达的方式可以提高学生的学习兴趣。

1 风力发电机模型

本文研究的是一台3 MW的水平轴变桨距风力机。把风电系统分为风力机模型、传动机构模型、发电机模型和变桨控制系统模型4个部分。

1.1 风力机气动模型

当风轮接收到风能时，风轮上的叶片会把风能转换成机械能带动传动系统进行工作。当风速低于切入风速时，桨距角β为0°，称为启动状态；当风速高于切出风速时，桨距角β为90°，称为顺桨状态；当风速高于切入风速低于额定风速时，称为欠功率状态；当风速高于额定风速低于切出风速时，称为额定功率状态。根据贝兹理论，风轮吸收的功率和风轮气动转矩为[3]

(1)

式中:Pw为风力机风轮的捕获功率；Tw为风力机的机械转矩；v为风速；ρ为空气密度；R为风轮半径；λ为叶尖速比；Cp为风能利用系数；CT为机械转矩系数，且有Cp(λ,β)=λCT(λ,β)；β为桨距角；A为过流面积。

在风力发电变桨控制系统中，风能利用系数Cp尤为重要，它可以看成是叶尖速比λ与桨距角β的一个非线性函数。在低风速段和高风速段都可以通过调节风能利用系数CP来实现风力机输出功率控制。Cp、λ和β三者之间的关系为：

(2)

1.2 传动机构模型

风力发电机的传动机构部分主要由风轮侧低速轴和发电机侧高速轴两部分组成，通过齿轮的啮合把低速轴的转速传到高速轴，带动发电机工作。传动机构模型的微分方程如式(3)～(5)所示。

(3)

式中:Jw为风轮转动惯量；Jg为发电机转动惯量；Td为阻力转矩；Tm为高速轴传给齿轮的转矩；且Td=s1+s2/ω+s3ω，其中s1、s2、s3为阻力转矩的3个系数；n为齿轮传动比；ωr为风轮转速；ωg为发电机转子转速；Te为发电机的电磁转矩。

为方便分析，假设传动轴为刚性传动，可得传动系统的总等效转动惯量为：

Jd=Jw+n2Jg

(4)

因为ωg=nωr，结合式(3)、(4)，可得风力发电机传动系统数学模型为：

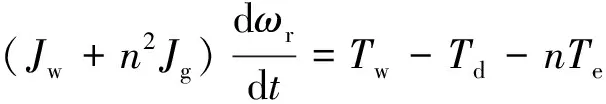
(5)

1.3 发电机模型

为方便发电机模型的研究，假设在理想情况下对异步发电机模型进行研究。异步发电机把从风轮获得的机械能转化成电能，根据文献[16]，其数学模型为：

(6)

式中:Te为发电机电磁转矩；p为发电机极对数；P为发电机输出功率；C1为修正系数；U1为发电机输出电压；m为相数；ω0和ωg分别为电机同步转速和发电机转子转速；r1和r2分别为定子和转子绕组等效电阻；X1和X2分别为定子和转子绕组电抗。

1.4 变桨控制系统模型

风力发电机变桨执行机构可简化成一阶惯性环节：

(7)

式中:Tβ是时间常数；βr为参考桨距角。

根据以上分析可将风电系统看成是一个二阶系统[4]:

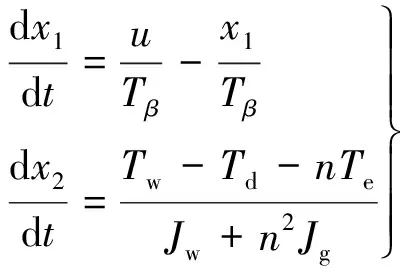
(8)

式中:桨距角β和风轮转速ω为系统的两个状态变量，即x=[x1,x2]T=[β,ω]T；把βr当作风力发电系统的桨距角参考输入，即u=βr。

2 常规PID变桨控制器设计

本文采用转速偏差和功率偏差作为双闭环反馈系统的两个输入进行控制。常规PID变桨控制系统设计如图1所示。

把转速偏差与功率偏差作为两个输入，建立一个双闭环的PID变桨控制系统。PID控制器分别对转速

图1 常规PID变桨距控制框图

偏差eω(t)=ωr(t)-ωt(t)与功率偏差ep(t)=Pr(t)-Pt(t)进行控制，通过参数调节，控制桨距角的大小，实现风电系统PID变桨控制[6]：

(9)

式中:Kp为比例系数；Ti为积分时间常数；Td为微分时间常数。

3 非线性扩张状态观测器PID变桨控制器设计

风力发电系统存在外部干扰和内部扰动时，系统会产生一定的误差。利用非线性扩张状态观测器对系统输出的桨距角信号和转速信号进行测量，将系统扰动量转换成新的状态变量，同时将观测器的输出信号快速反馈到输入端进行实时补偿，使观测信号与输入端状态变量的估计误差逐渐逼近于零，从而实现对PID变桨系统的补偿。图2为非线性扩张状态观测器PID变桨控制系统框图。

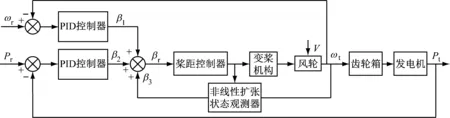
图2 NESO-PID变桨距控制框图

3.1 基于非线性扩张状态观测器的变桨系统设计

针对系统内部、外部不确定因素无法测量等问题，韩京清教授设计出一种不确定对象的非线性扩张状态观测器[14-15]：

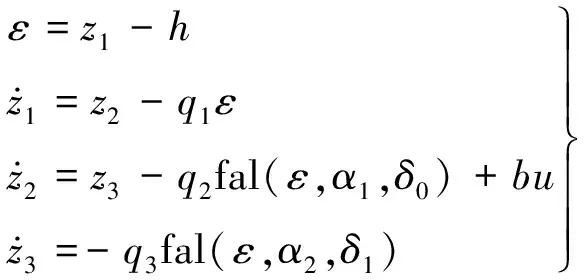
(10)

式中:z1为系统状态变量的估计值；z2为状态变量导数的估计值；z3为系统总扰动估计值；qi>0(i=1,2,3)为观测器的增益；ε为观测器的观测误差；非线性函数fal(ε,αi,δ)起抑制信号抖振作用，可表示为：

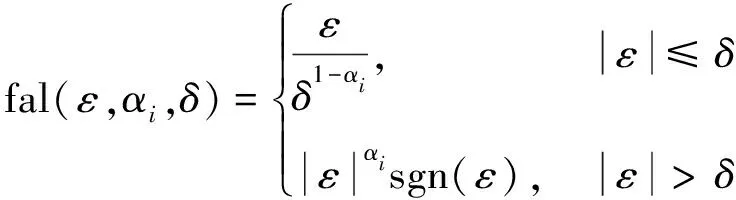
(11)

式中:i=1,2；0<αi<1；δ>0表示线性区间的长度，非线性函数fal(ε,αi,δ)产生的增益高低与观测误差ε密切相关，ε的值越小则非线性函数产生的增益越高，反之则越低。

当观测器增益qi一定时，结合式(10)、(11)，观测器的观测有：z1(t)→m1(t)；z2(t)→m2(t)；z3(t)→m3(t)=f1(m1,m2)+(b-b0)u(t)，b0是b的估计值，b0=133。文献[11]中指出，观测误差ε可以收敛到一个很小的值，即|zi-yi|≤di，di>0为一个趋近于0的正数。

为观测器能够更好的测量系统外部干扰和内部扰动，以及实时对输入端进行反馈补偿，根据文献[12]，把风电系统看成一个二阶非线性系统:

(12)

式中:f(m1,m2)、ω(t)分别为系统的内部扰动和外部扰动；m1、m2分别为系统的两个状态变量；y、u分别为系统的输出和控制器产生的系统控制量。

根据文献[7]，可以得出二阶非线性扩张状态观测器的变桨距控制规律为：

(13)

式中:z1是系统状态变量ω的估计值，即y=ω；z2是ω导数的估计值；z3是系统总扰动的估计值，z3=f(m1,m2)+(b-b0)u；ξp、ξd为控制器需要整定的参数，ξp=6.0，ξd=1.5；v为系统参考输入。

综上所述，得出非线性扩张状态观测器PID变桨系统的控制律为：

ut=β1+β2+β3

(14)

3.2 非线性扩张状态观测器的变桨仿真模型

本双闭环变桨控制系统输入端采用PID控制器对转速偏差和功率偏差进行控制[16]，变桨部分采用非线性扩张状态观测器进行系统观测，把测量的桨距角信号和转速信号作为扩张状态观测器的两个新状态变量，通过观测器的测量和控制，得到桨距角和转速的输出信号，将他们输入到风力发电系统中得到功率值，同时把观测器输出的转速信号和桨距角信号反馈到输入端进行实时补偿，使观测信号与输入端状态信号的估计误差逐渐逼近于零，从而实现输出功率控制。图3所示为非线性扩张状态观测器PID变桨控制的Simulink仿真模型。

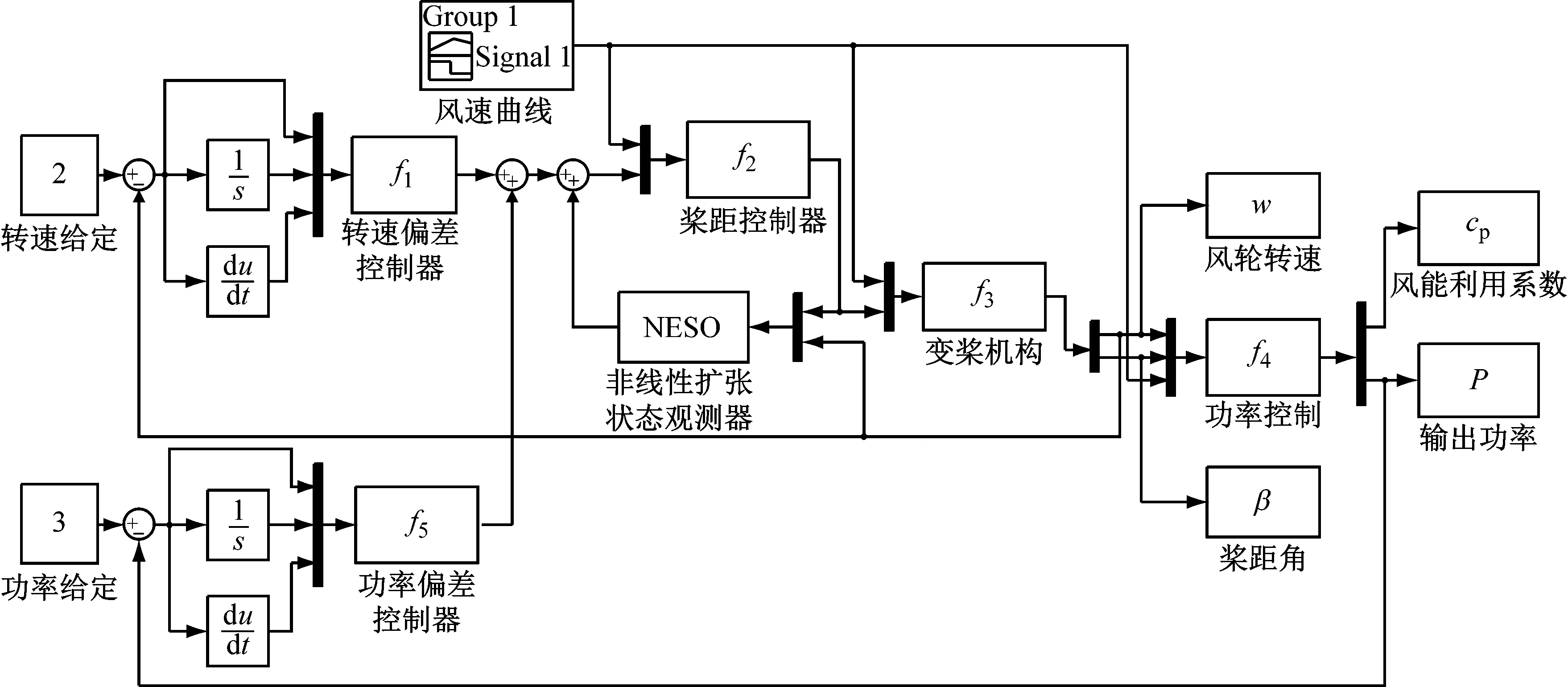
图3 NESO-PID变桨控制的Simulink仿真模型

4 仿真实验与结果分析

4.1 仿真实验数据

为了验证所建模型和算法的有效性，并加深学生对知识的理解，采用Matlab/Simulink仿真软件进行验证。风力发电机的参数见表1，控制系统的参数见表2。

4.2 仿真结果与分析

以额定功率为3 MW的风力发电机为研究对象，以风速、转速偏差和功率偏差为输入，以电机功率为输出，根据风电系统数学模型，建立Matlab/Simulink仿真模型。

为了验证非线性扩张状态观测器PID变桨控制的优越性，设计了两种变桨距控制器进行对比，即：常规PID变桨控制器；非线性扩张状态观测器PID变桨控制器。在非线性扩张状态观测器PID变桨控制器中，转速偏差PID控制器的参数为Kp=31，Ki=0.01，Kd=0，功率偏差PID控制器的参数为Kp=7，Ki=0.2，Kd=0。

在风速高于额定风速的情况下进行风电系统变桨控制研究，额定风速为12 m/s，其风速曲线变化如图4所示。在0～10 s，风速为恒定值13.5 m/s，在第10 s时刻，风速突然增大到14 m/s，然后一直保持到第25 s，又突然增大到14.5 m/s，保持到第40 s结束。

表1 风力发电机仿真参数

表2 控制系统参数

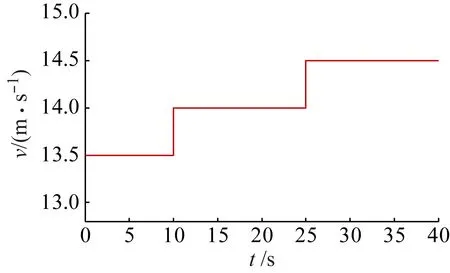
图4 高于额定风速的风速曲线

在两种变桨距控制器控制下，桨距角的仿真结果如图5所示，风轮转速的仿真结果如图6所示，风能利用系数的仿真结果如图7所示，输出功率的仿真结果如图8所示。

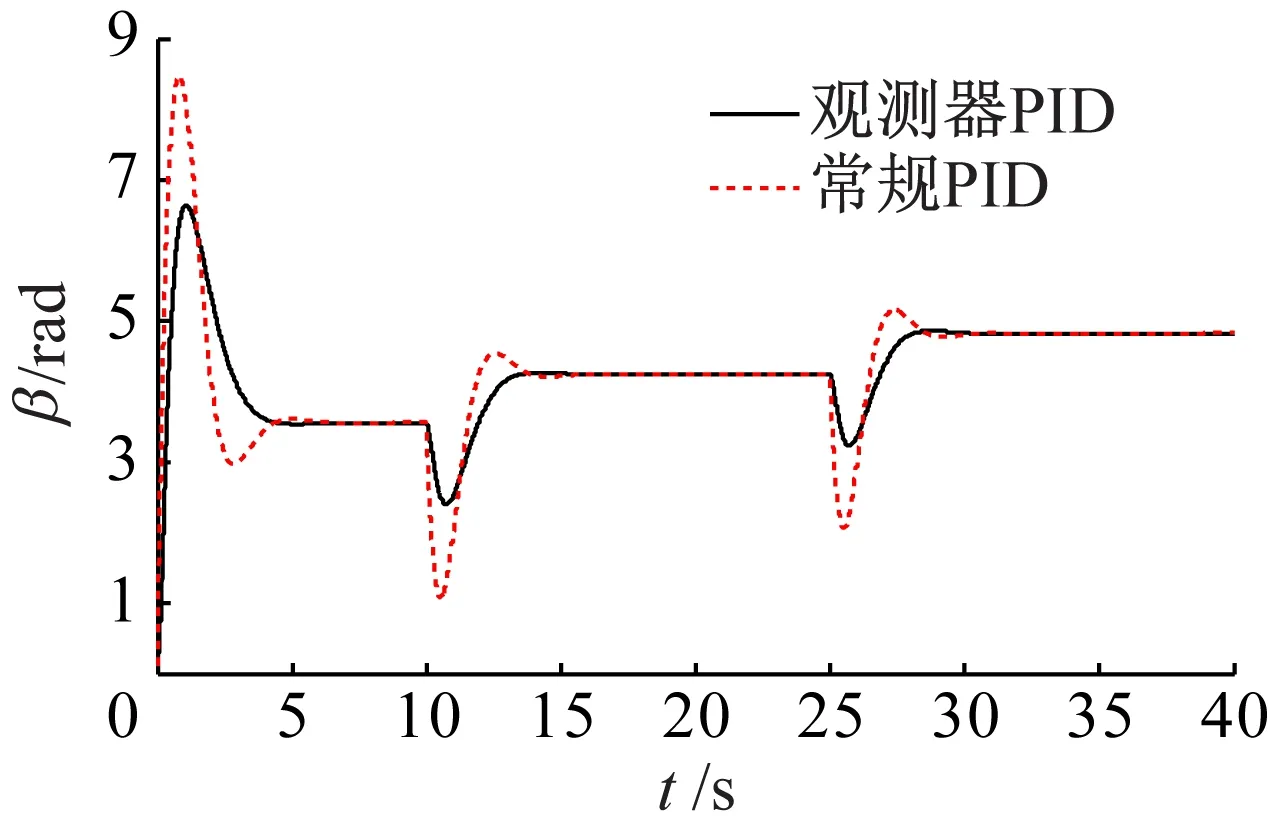
图5 桨距角曲线变化对比图

图6 风轮转速曲线变化对比图

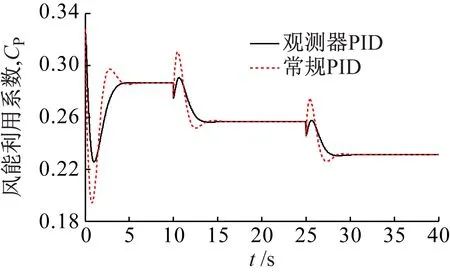
图7 风能利用系数曲线变化对比图

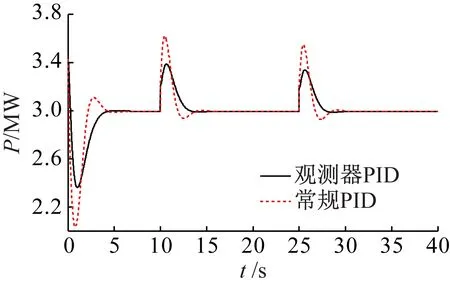
图8 输出功率曲线变化对比图

从图5可以看出，当风速发生突变时，与常规PID变桨控制相比，本文提出的非线性扩张状态观测器PID变桨控制输出的桨距角波动幅度小，响应快，能够快速的把系统调节到稳定状态。从图6可以看出，两种变桨控制输出的转速都在额定转速附近波动，但采用常规PID变桨控制的转速波动比较大，而且调节时间比较长，导致输出功率也受到影响。从图7可以看出，采用非线性扩张状态观测器PID变桨控制可以快速调节桨距角来改变风能利用系数，从而使输出功率快速向额定功率附近靠近。从图8可以看出，当超过额定风速的风速曲线发生突变时，相比常规PID变桨控制，非线性扩张状态观测器PID变桨控制响应速度快，调节时间短，能够快速的把输出功率调节到额定功率值附近，具有更好的稳定性和动态特性。

5 结 语

综合仿真结果可以得出，当风速高于额定风速时，相对于常规PID变桨控制，非线性扩张状态观测器PID变桨控制可以通过快速的调节桨距角来使输出功率保持在额定功率附近，能够有效克服非线性和时变性的影响，表现出较好的动态特性和鲁棒性，改善了变桨距控制性能。