库水作用下滑坡体内侵蚀特性的数值模拟

王平凡， 毕金锋， 罗先启

(上海交通大学 船舶海洋与建筑工程学院，上海 200240)

0 引 言

堤坝结构或边坡工程长期受到库水位或降雨的影响，土体结构由于渗流影响会发生内部失稳，内侵蚀作用已经成为导致溃坝及滑坡的主要因素之一。如1998年，长江九江段4号闸与5号闸之间决堤，溃口发生前堤防下游坡后有较多渗透变形迹象，随后发展为堤防溃口。

目前，在诸多研究土体内侵蚀的试验中，主要研究的是影响内侵蚀的因素和细颗粒流失规律。Benamar等[1]在不同的流动条件和土体力学参数下进行渗流试验，研究内侵蚀的发生机理和动力学特性；李喜安等[2]利用解析方法推导内侵蚀发生的临界条件，指出内侵蚀发生的临界条件应由具体受力情况来分析；Marot等[3]研究内侵蚀过程中土体密度、孔隙压力和被侵蚀颗粒的质量变化，表明细颗粒流失导致孔隙压力增加，进而出现局部失稳；Chang等[4]对内侵蚀试样进行三轴压缩试验，测试土体力学特性受内侵蚀作用的影响程度，当细颗粒流失量达到一定量级后，土体由剪胀变为剪缩。Bonelli等[5]对管涌中细颗粒流失规律进行研究，建立流体、被侵蚀颗粒和土体整体的质量守恒方程；Sterpi[6]提出一种计算细颗粒流失速率的方法，通过可被侵蚀细颗粒的质量计算在任意时刻下被侵蚀的细颗粒的质量；吴梦喜等[7]对细颗粒流失量不同的土体进行三轴和侧限压缩试验，将土体的应变增量分成由应力和模量衰化引起的应变增量。

另外，还有学者借助有限元模拟内侵蚀过程来分析内侵蚀特性。Sibille等[8]利用离散元和格子波尔兹曼法来模拟内侵蚀过程中细颗粒从骨架颗粒脱离并随水流运移，通过流体作用在颗粒上的功来耦合两者之间的相互作用；Zhang等[9]根据热力学原理和多孔介质理论建立内侵蚀结构模型，解释管涌现象在临界水力梯度的区域加剧原因；Sterpi[6]结合被侵蚀颗粒的质量守恒方程和基于渗流实验得到的侵蚀规律，建立起细颗粒侵蚀与运移的有限元模型；刘忠玉等[10]建立临界水头梯度与细颗粒流失的关系，采用有限元方法分析细颗粒流失对工程稳定性的影响。罗玉龙等[11]结合潜蚀本构方程和土体三相质量守恒方程，建立有限元数值模型研究管涌过程中的内侵蚀作用。

在上述文献中，试验所采用的样本是重塑土，这与天然土存在较大的差异，试验得到的内侵蚀开始和结束条件与真实情况有些许差别。而且有限元模拟采用的控制方程没有将质量守恒方程、连续性方程、渗流控制方程耦合起来，只是单独考虑一个方面或只是耦合了其中两个控制方程。本文参考其他学者所做的细颗粒流失试验和内侵蚀控制方程，以锦屏呷爬滑坡为例，采用有限元的方法，耦合质量守恒方程、连续性方程和渗流方程建立改进后的内侵蚀数值模型，研究内侵蚀发生时不同的水头对土体的孔隙率、被侵蚀颗粒的质量、细颗粒流失速率的影响。

1 内侵蚀形成条件

水流流过土体内部而将细颗粒带走的现象称为内侵蚀。内侵蚀过程中，土体内部细颗粒在渗透力作用下发生松动并脱离主骨架，从而造成土体的局部孔隙率增大，随着水对土体的内侵蚀作用的加剧，会在局部形成优势路径或孔洞，土体骨架遭到破坏，局部强度削弱，容易造成土体整体在优势路径所在平面上发生剪切破坏。

沙金煊[12]通过对作用在单个土颗粒上的渗透力的计算，提出渗透侵蚀临界水力坡降的近似公式

(1)

式中：r为可被侵蚀颗粒粒径;k为渗透系数;φ为孔隙率。

《水利水电工程地质勘察规范》中对于间断级配的土体，以间断区间的中间值作为可被侵蚀的细颗粒的粒径。根据锦屏一级水电站坝址相关勘察报告及工程经验，确定呷爬滑坡可被侵蚀的细颗粒最小粒径为1 mm。滑坡体的渗透系数约为0.3 mm/s，孔隙率约为0.3，故发生内部侵蚀的临界水力坡降约为0.398。

图1为库水位线处的水力梯度变化图，从图中可以看出，随着库水位的变化，水位线处的水力梯度大致在0.52～0.65范围内变化，大于临界水力坡降，所以在库水位以下的滑坡体内会发生内侵蚀现象。为了模拟出滑坡体在内侵蚀过程中土体的孔隙率、被侵蚀颗粒的质量、细颗粒流失速率等，需要建立相应的内侵蚀控制方程。

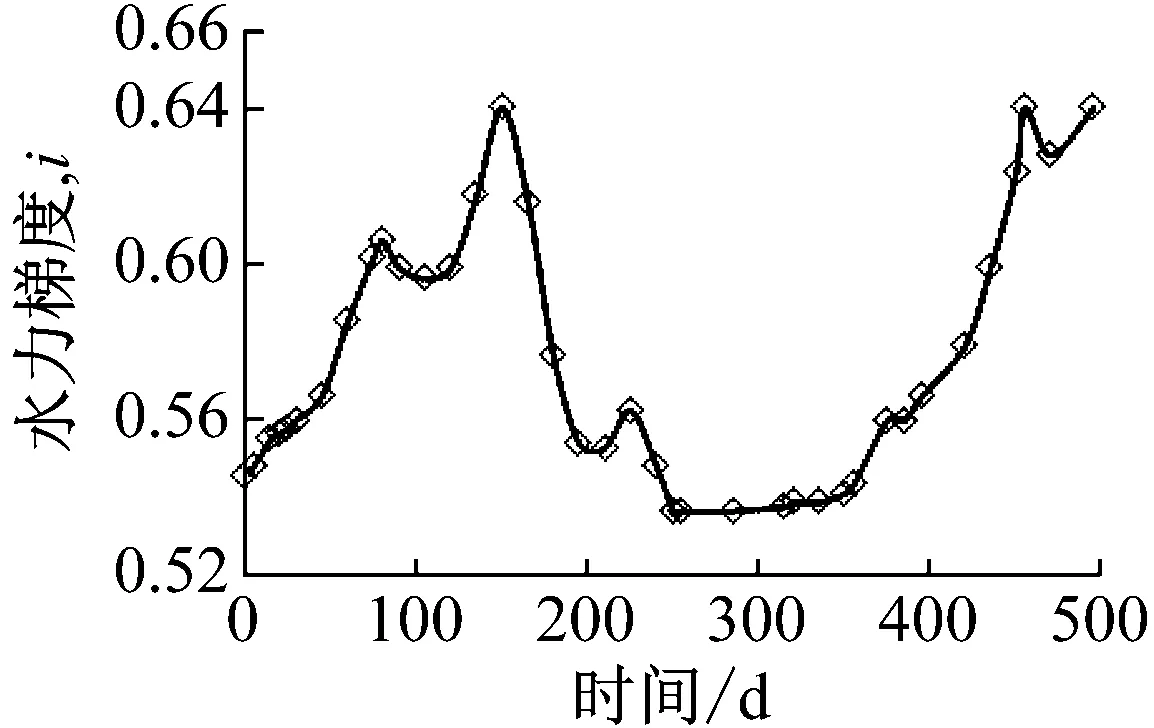
图1 水力梯度变化图

2 内侵蚀控制方程

2.1 内侵蚀下的质量守恒方程

在内侵蚀过程中，细颗粒从土体骨架脱离出来并随水运动。假设其运动速度与水的流速一致，Cividini等[13]利用质量守恒定律得到内侵蚀作用的连续性方程：

(2)

式中：ρtr为被侵蚀的细颗粒的密度；vi为被侵蚀颗粒在i方向上的移动速度；qe为单位体积细颗粒被侵蚀的速率；qdp为被侵蚀颗粒沉积到土骨架的速率。

Vardoulakis等[14]将饱和多孔介质单元体分为未被侵蚀的土体、水和被侵蚀的细颗粒三部分,质量分别为dMs，dMw，dMfs，体积分别为dVs，dVw，dVfs。当有细颗粒被侵蚀时，细颗粒随水一起流动，被侵蚀的颗粒和水组成的流动体密度为

(3)

式中：ρs为土颗粒的密度；ρw为水的密度；c为被侵蚀细颗粒的体积分数。被侵蚀颗粒的密度为

(4)

将式(4)代入(2)，则内侵蚀作用的连续性控制方程可以改写为

(5)

2.2 内侵蚀下的渗流方程

发生内侵蚀时，土体内渗流状态十分复杂，达西流、非达西流、优势流可同时存在，且描述土体渗流状态的方程也不尽相同。但在内侵蚀发生的初期，土体中的渗流以达西流为主，故本文采用达西定律来表示内侵蚀下的渗流方程，即

Vw=k▽p

(6)

Kozeny-Carman公式是描述多孔介质的渗透率与孔隙率关系精度最高的经验公式，其表达式为

(7)

式中：η为Kozeny常数，将初始渗透率k0和初始孔隙率φ0代入上式，可得

(8)

则式(5)可以写为

(9)

随着内侵蚀的发生，流速增大，雷诺数随之增大，流体的渗流速度与水力梯度之间将不再呈线性关系，达西定律不再适用，可改用福希海默方程[15]等描述非达西流的渗流方程。

2.3 内侵蚀速率

Cividini等[16]根据对重塑土样的室内试验，认为在一定水力梯度下一直对土体进行内侵蚀作用，最终也不会将全部的细颗粒带走，而是会有细颗粒残留在土体内。在渗透作用下，土体内部的细颗粒被侵蚀，被侵蚀的颗粒粒径由小变大。所以设土体的骨架可被侵蚀的最大颗粒为rmax，可被侵蚀的颗粒最小粒径为rmin。如果rrmin时，则细颗粒有可能被侵蚀出来。所以，本文考虑在呷爬滑坡土体级配曲线上，只有颗粒粒径在rmin和rmax之间的颗粒才考虑内侵蚀速率。

(10)

式中，土体的体积变化率为

(11)

(12)

式中：φ为侵蚀后土体孔隙率，

φ=dVfs/dVs+dVw

3 呷爬滑坡内侵蚀特性分析

3.1 基本情况

锦屏呷爬滑坡位于锦屏一级水电站坝址上游11.5 km，前缘高程1.655 km，与枯期河水位持平，后缘高程2.120 km，滑坡纵长约880 m，宽约260～300 m，滑体平均厚度约60 m，体积约1.3×107m3。滑体物质主要为块碎石土，滑带厚1～8 m，主要由灰黑色泥夹碎石组成[17]。

前期勘察表明：呷爬滑坡除水库蓄水至正常蓄水位(1.880 km高程)或迭加VII度地震时，滑体有滑动的可能，其余工况均能保持稳定或基本稳定，根据滑体物质组成及现今地形特点分析，预计失稳方式将以逐级牵引式滑塌为主。

水库蓄水期，呷爬滑坡前缘见小规模次级滑塌，整体未见明显变形破坏迹象。2015年11月水库第2次蓄水至1.880 km后调查，发现呷爬滑坡产生整体蠕滑，在高程约1.900、2.050 km及后缘地带出现贯通性拉裂缝。直至2017年6月库水位消落至1.800 km后调查，发现呷爬滑坡仍在整体滑移，坡体原有拉张裂缝的下错幅度有明显增加，其中，最后缘贯通裂缝最大下座高度已大于200 cm，较2016年1.800 km水位调查时增加约50～70 cm，表明呷爬滑坡的变形仍在增加。该呷爬滑坡的地形图和地质剖面图如图2和图3所示。

图3 呷爬滑坡地质剖面图

3.2 内侵蚀特性分析

本文利用COMSOL Multiphysics软件建立有限元模型，求解渗流和侵蚀耦合控制方程组，即式(5)、(6)和(12)。

根据图2的滑坡地形图和图3的地质剖面图,忽略滑坡的中上部裂缝与后缘裂缝，建立数值分析的模型。在数值模型中，认为水为不可压缩流体，固体颗粒的压缩量极小可以忽略，并且不考虑流体中含有细颗粒时对黏滞系数的影响，根据实验结果和级配曲线，各参数取值如下:ρw=1 000 kg/m3,Es=80 MPa,μw=1.0 mPa·s,νs=0.35,φbr=0.2,φs=0.348 3,Kbr=0.01 mm/s,ρs=2 100 kg/m3,k0=0.4 mm/s,rmin=1 mm/s,φ0=0.3,rmax=6 mm。

整个模拟试验过程持续525 d，水头边界条件根据实测的变化情况施加在模型边界上。滑坡体表面为透水边界，滑带为不透水边界，初始水头边界条件根据实测水位取值；孔隙率的初始条件设置为φ0；试验开始时的水头与试样的上边界一致，初始速度场v为0；在考虑重力的情况下，模型内部的初始压力为重力产生的压力场，即p0=ρwgz。

根据数值模拟的结果可以得到滑坡体在库水位作用下的渗透率k、被侵蚀颗粒的体积分数φ以及内侵蚀速率qe的变化情况。

图4为1.80 km和1.84 km高程处在库水位变化情况下，滑坡体内渗透率k的变化情况。1.80 km是测量周期内的最低水位，此处始终受到内侵蚀的作用。从图中可以看出，在内侵蚀持续作用的整个过程中，不断有细颗粒被侵蚀，滑坡体的渗透率一直在增大且逐渐趋于平稳。内侵蚀发生的初期0～200 d，渗透率的斜率较大，表明有大量粒径大于rmin的可被侵蚀颗粒被水流冲刷带走；中期200～450 d内，由于小粒径的颗粒逐渐变少以及颗粒在渗流通道内的累积，渗透率的变化趋势变缓；450 d以后，大部分可被侵蚀颗粒都被侵蚀掉了，但仍有少量粒径接近rmax的颗粒被侵蚀，此时内侵蚀作用效果逐渐减弱，渗透率也趋于平稳，最终将保持不变。在1.84 km高程处的渗透率与1.80 km处的渗透率变化规律相似，但在75～165 d及405 d以后，库水位在1.84 km以下，所以此时高程1.84 km处不受库水位的作用，内侵蚀作用暂时停止，被侵蚀颗粒的量为0，在图中表现为渗透率曲线保持水平状态。当库水位再次超过1.84 km时，内侵蚀又再次发生。由于越往下的部分受到库水作用的时间就越长，受到内侵蚀的时间越来越长，渗透率越大，故1.80 km高程处的渗透率比1.84 km高程处的渗透率大。

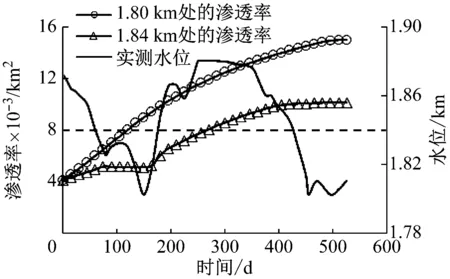
图4 滑坡体内渗透率的变化

图5为不同高程下滑坡体内可被侵蚀颗粒的侵蚀量占土体的体积分数φ，与渗透率的变化规律基本一致。1.80 km高程处完全处于水下，受到的内侵蚀时间最长，被侵蚀的细颗粒越多。可被侵蚀颗粒占土体的体积分数的定义与孔隙率的定义类似，对于颗粒粒径小于rmax的颗粒可以看作在内侵蚀发生之前就已经被侵蚀掉了，此时的可被侵蚀颗粒的体积分数相当于土体的初始孔隙率0.3，对于粒径处于rmin和rmax之间的颗粒，则需要在库水的作用下被侵蚀掉。从图中的趋势线可以看出，如果在525 d之后库水位超过1.84 km，那么1.84 km高程处的可被侵蚀颗粒的φ将沿着原来的增长趋势继续增加，最终将和1.80 km高程处的φ值趋于同一个稳定的φmax。当所有可被侵蚀的颗粒全部被侵蚀完之后，内侵蚀结束。

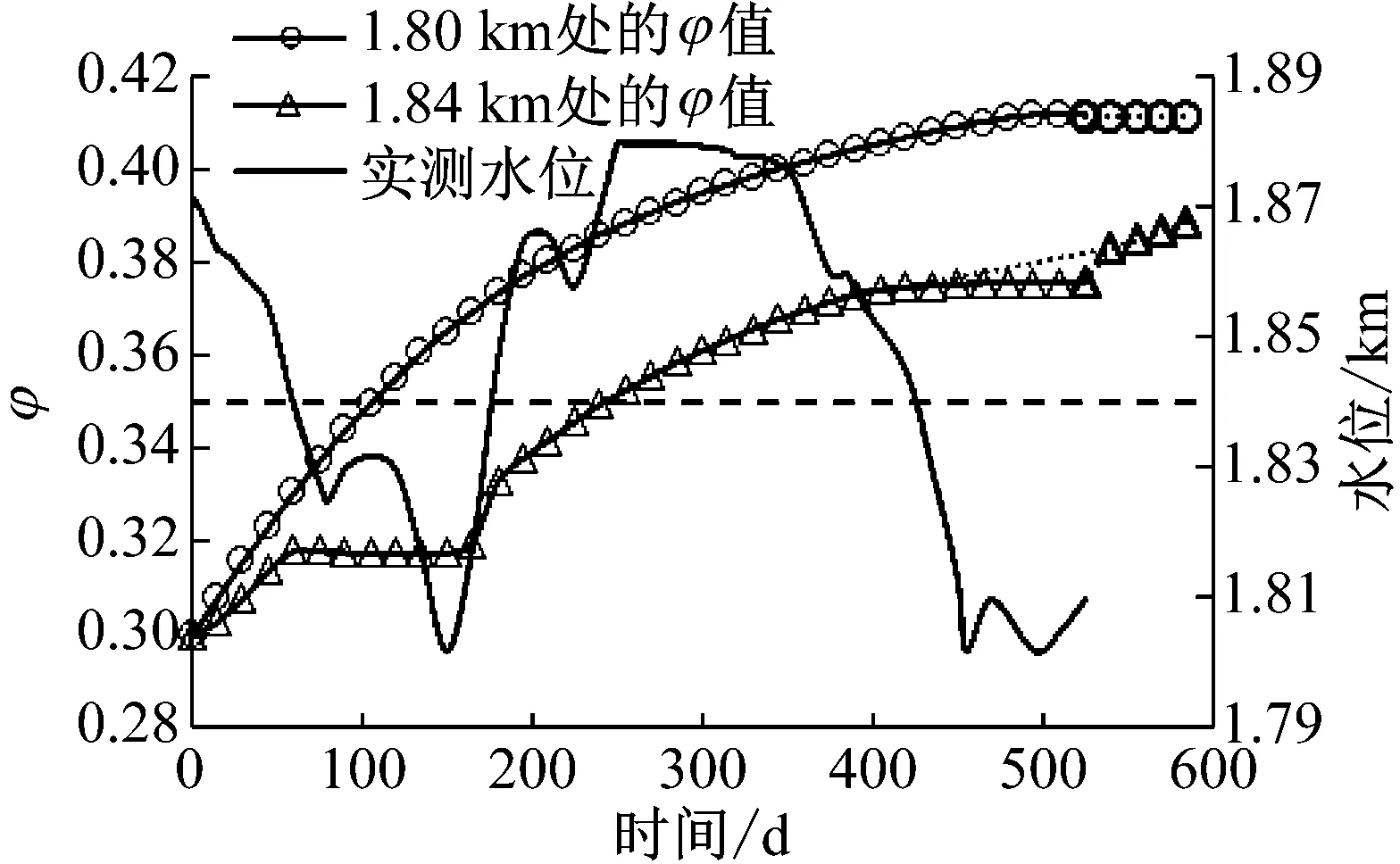
图5 滑坡体内可被侵蚀颗粒体积分数的变化

图6为库水位对内侵蚀速率qe的影响规律。从图中数值模拟结果可以看出，由于初始孔隙率的存在，临界粒径rmin的颗粒很容易通过土体内部原有的孔隙被水流冲刷带出，所以在内侵蚀发生的初期的0～30 d内，内侵蚀速率是增加的。从总的趋势来看，随着细颗粒不断被侵蚀，可被侵蚀的颗粒越来越少，内侵蚀速率是持续下降的，直到所有可被侵蚀的颗粒被侵蚀完之后，内侵蚀速率变为0，内侵蚀过程结束。其中，在75～165 d及405 d以后，1.84 km高程处的水位是低于1.84 km的，此时的内侵蚀速率为0，渗透率k和可被侵蚀颗粒的φ保持不变，这与图4和5中表现的规律是一致的。本文所考虑的内侵蚀速率是由可被侵蚀但仍未被侵蚀的颗粒含量决定的，同一时间，高程越低的地方受库水影响的时间就越长，被侵蚀颗粒的量越多，可被侵蚀但还未被侵蚀的颗粒就越少，导致内侵蚀速率越来越小，故在图6中体现出的是在同一时间下，绝对水位是一定的，高程高的地方，由于受库水的影响时间少，未被侵蚀的颗粒含量仍很高，故内侵蚀速率较高程低的地方大。

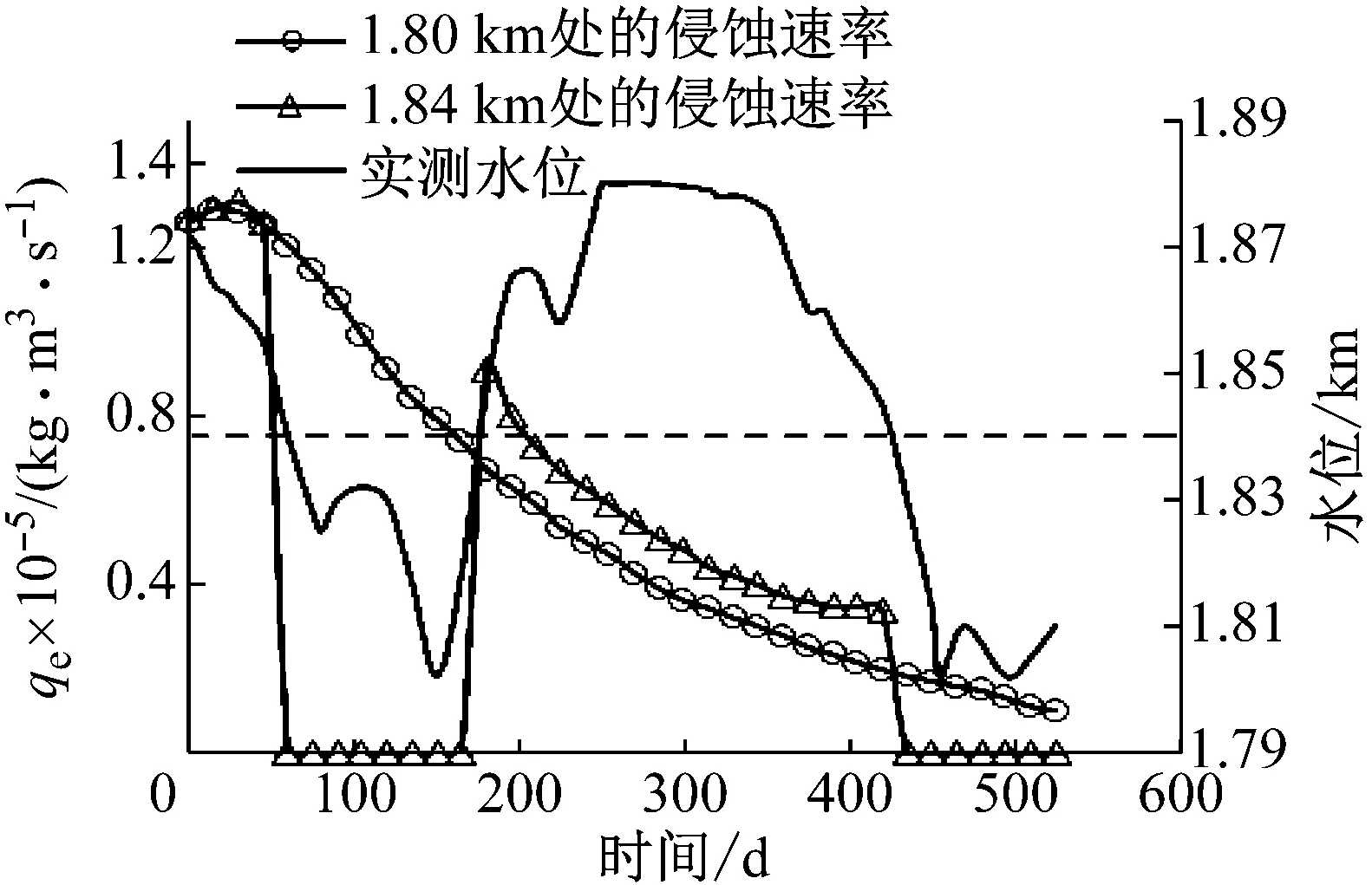
图6 内侵蚀速率的变化

4 结 论

本文对库水位作用下土体内侵蚀特性进行了研究，总结如下：

(1) 根据质量守恒方程，建立连续性方程、渗流方程和内侵蚀速率。初步考虑土体的颗粒级配对内侵蚀影响，以可被侵蚀的最小颗粒粒径rmin和可被侵蚀的最大颗粒粒径rmax来控制受内侵蚀作用影响的范围。当rrmin时，则细颗粒有可能被侵蚀出来。

(2) 以锦屏呷爬滑坡滑体为研究对象，利用COMSOL Multiphysics软件建立有限元模型，耦合上述土体内侵蚀过程中被侵蚀颗粒的质量守恒方程、内侵蚀的渗流方程和考虑级配影响的内侵蚀速率。模拟结果表明土体孔隙率和被侵蚀颗粒的体积分数在内侵蚀作用下不断增加，当所有可被侵蚀的颗粒都被冲刷掉之后，细颗粒的流失速率最终趋于稳定。而且某一高程处的内侵蚀作用会在水位低于此处高程时暂时停止，当水位重新超过此处高程时，内侵蚀作用会继续沿着原来的趋势进行下去。但是该模型未考虑非达西流情况下，即渗透速率与水力梯度呈现非线性增长时的变化情况，以及未考虑水位变化速率的影响。

(3) 该呷爬滑坡的前缘长期处于水下，数值模拟结果显示处于水下的部分始终受到内侵蚀的影响，细颗粒在不断的流失，孔隙率持续增大，直至滑坡失稳。因此本文的研究可以用于大致确定滑坡体正处于内侵蚀的哪个阶段和水下部分的细颗粒流失程度，对实时监测滑坡的稳定性有一定的实际意义。