逐次Taylor替换与一类幂指函数不等式的机器证明

陈世平，陈 果

（1.中国民航飞行学院德阳校区-四川省商贸学校，四川 德阳 618000；2.西南科技大学信息工程学院，四川 绵阳 612000）

0 引 言

Nishizawa 证明了[10]：

Branko Maleševic 等证明了文献[10]提出的公开问题[11]：

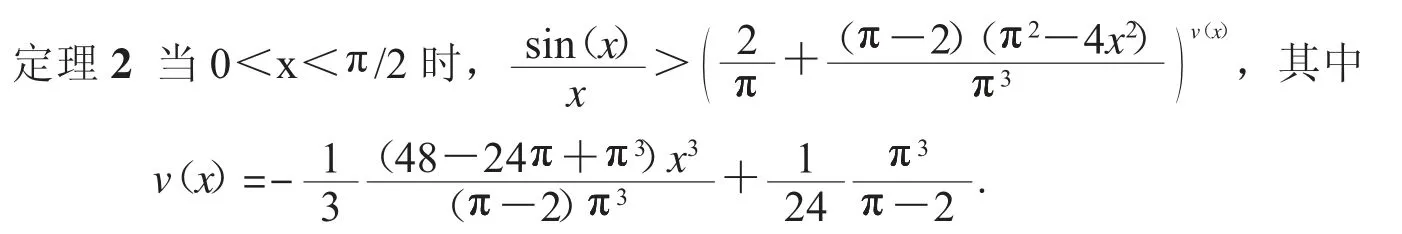
文献[12-17]讨论了形如f（x，trans1（x），…，transn（x））＞0 的超越多项式不等式的机器证明，其中f（x，x1，…，xn）是n＋1 元多项式，trans1（x）可以是初等超越函数，如sin x、cos x、tan x、arcsin x、arccos x、arctan x、ex、ln x 等，也可以是形如trans1（trans2（x））的复合函数，利用一次或多次Taylor 替换，目标不等式的证明转化为一系列单变量的多项式不等式的验证，然后由代数不等式证明软件BOTTEMA 完成.算法对于常见的超越多项式不等式非常有效，而且是“可读的”，可以输出能够理解的证明过程.这种方案被称为逐次Taylor 替换法.

本文的目的是讨论定理2 中不等式的机器证明，这是一个比文献[12-17]中引用的例子更复杂、超越多项式不等式范围外形如sin（x）/x＞u（x）v(x)的幂指函数不等式问题，运用逐次Taylor 替换并结合人工证明和巧妙的变量代换，实现了该不等式的机器证明.通过与文献[11]不同的途径，也证明了文献[10]提出的公开问题，尽管结论是已知的结果，但方法本身对于同类不等式具有示范性.

此外，算法输出的证明过程中除了有的需要判定其正定性的一元有理多项式次数较高从而验证计算量较大外，其余内容都容易“手工”验算.

1 逐次Taylor替换

不等式的自动证明问题，一直以来都是数学机械化和自动推理领域研究热点和难点问题.近年来，代数不等式的自动证明吸引了大批学者研究，也取得了丰富的成果，已有专著《不等式机器证明与自动发现》问世，特别是杨路教授提出了降维算法，据之编制的通用程序BOTTEMA 能够成批验证不等式，但BOTTEMA 只能处理代数不等式或先把几何不等式转化为代数不等式，尚不能解决一般的超越不等式自动证明问题[18-22].当然关于超越不等式已有了大量的研究成果和证明方法，但这些成果和方法尚不能适应数学机械化和推理自动化的需要，故有必要对此类不等式的自动证明进行专门的研究，探索新的算法.

1.1 Taylor替换

给定（n＋1）元实系数多项式环R[x，x1，…，xn]，定义该环上一个映射：hom:f（x，x1，…，xn）→F（x），将变量xi用某个超越函数transi（x）代替.

定义1.1 给定（n＋1）元实系数多项式f（x，x1，…，xn），它在映射hom 下的像F（x）=hom（f）=f（x，trans1（x），…，transn（x））称为超越函数多项式，称transi（x）为其超越因子.

如x＋sin（x）、x＋cos（sqrt（x））、x＋esin(x)、x＋arctan（x）-arcsin（x）都是超越函数多项式，sin（x）、cos（sqrt（x））、esin(x)、arctan（x）、arcsin（x）就是函数的超越因子.

定义 1.2 对于超越函数 F（x），在某个区间 I，如果有代数函数列{T_min（n，F）}和{T_max（n，F）}，存在自然数 n0，当 n≥n0时，满足：

1）T_min（n＋1，F）＞T_min（n，F），且当 n→∞ 时，T_min（n，F）→F（x）；

2）T_max（n＋1，F）＜T_max（n，F），且当 n→∞ 时，T_max（n，F）→F（x）.

我们称{T_min（n，F）}和{T_max（n，F）}为 F（x）在区间 I 的下限多项式列和上限多项式列，T_min（n，F）为 F（x）的下限多项式，T_max（n，F）为 F（x）的上限多项式，n0称为临界值.

显然，F（x）的下限多项式和上限多项式满足：

T_min（n0，F）（x）＜T_min（n0＋1，F）（x）＜T_min（n0＋2，F）（x）＜…＜F（x）＜…＜T_max（n0＋2，F）（x）＜T_max（n0＋1，F）（x）＜T_max（n0，F）（x），也就是说若 F（x）存在有下限多项式列和上限多项式列，则有一个多项式套来逼近 F（x）:（T_min（n0，F）（x），T_max（n0，F）（x））⊃（T_min（n0＋1，F）（x），T_max（n0＋1，F）（x））⊃（T_min（n0＋2，F）（x），T_max（n0＋2，F）（x））⊃……⊃{F（x）}.

下面我们讨论如何计算或构造超越函数多项式F（x）=f（x，trans（x））的下限多项式和上限多项式（其中f（x，y）为二元多项式）.

为方便，我们将函数f（x）在0 点的Taylor 展开式中的前n 项之和记为taylor（f，n）.

定义1.3 如果超越函数f（x）在某个区间（0，T］满足以下条件：（1）大于0；（2）在0 点的Taylor 展开式收敛于f（x）；（3）taylor（f，n）可以表示为交错级数f1（x）-f2（x）＋f3（x）＋…＋（-1）n-1fn（x），其中fn（x）=An*x＾mn，0＜An≤1，mn-1＜mn；（4）存在常数n0，当n≥n0时，taylor（f，n）＞0，fn（x）＞fn＋1（x）＞0.我们称f（x）在区间（0，T］内可以规范展开，常数n0称为其临界值.若还满足An≤1/（n-1）!，则称f（x）在区间（0，T］内可以强规范展开.

常见的基本初等超越函数大都可以在相应的区间内规范展开：

arctan（x）=x-x3/3＋x5/5-x7/7＋…＋（-1）n-1x2n-1/（2n-1）＋……在区间（0，1］可以规范展开，临界值n0=1；

e-x=1-x＋x2/2!-x3/3!＋…＋（-x）n-1/（n-1）！＋……，在区间（0，T］（T 为任意正数，下同）可以规范展开，临界值n0=min{n∈N，当0＜x≤T 时taylor（e-x，n）＞0，taylor（e-x，n＋1）＞0，n＞T}；

ln（1＋x）=x-x2/2＋x3/3-……＋在区间（0，1］可以规范展开，临界值n0=1；

sin（x）=x-x3/3!＋x5/5!-……＋在区间（0，T］可以规范展开，其中临界值n0=min{n∈N，当0＜x≤T 时taylor（sin（x），n）＞0，taylor（sin（x），n＋1）＞0 且2n（2n＋1）＞T2}，特别地，当时，n0=1；

cos（x）=1-x2/2!＋x4/4!-……＋在区间（0，T］可以规范展开，其中临界值n0=min{n∈N，当0＜x≤T 时taylor（cos（x），n）＞0，taylor（cos（x），n＋1）＞0 且 2n（2n-1）＞T2}.我们注意到，当时，taylor（cos（x），2n）＜cos（x）=0，所以 cos（x）在内不能规范展开；

（1＋x）a=1＋ax＋a（a-1）x2/2!＋a（a-1）（a-2）x3/3!＋C（a，n）xn＋…，在区间（0，1）可以规范展开（其中 C（a，n）=a（a-1）（a-2）…（a-n＋1））.当 0＜a＜1 时，n0=1（展开式中f1（x）=1＋ax）.

其中 e-x、sin（x）、cos（x）在相应区间内还可强规范展开.

也有一些基本初等超越函数不能规范展开，如：

ln（1-x）=-x-x2/2-x3/3-……-xk/k-……（0＜x＜1）；

tan（x）=ΣB2n（-4）n（1-4n）x(2n-1)/（2n）!=x＋（1/3）x3＋（2/15）x5＋（17/315）x7＋（62/2835）x9＋……

引理1.1 如果f（x）区间I 可以规范展开，临界值为n0，则当n＞n0时，在区间I 上

1）taylor（f，2n-2）＜taylor（f，2n）＜f（x）；

2）taylor（f，2n-1）＞taylor（f，2n＋1）＞f（x）；

3）当n→∞时，taylor（f，n）→f（x）.

为方便，引入如下记号：

acrtan_max（x，n）=taylor（arctan（x），2n＋1），arctan_min（x，n）=taylor（arctan（x），2n），则当 x∈（0，1］，对任意 n∈N，arctan_max（x，n）＞arctan（x）＞arctan_min（x，n）；

ln_max（x，n）=taylor（ln（1＋x），2n＋1），ln_min（x，n）=taylor（ln（1＋x），2n），则当x∈（0，1），对任意 n∈N，ln_max（x，n）＞ln（1＋x）＞ln_min（x，n）；

sin_max（x，n）=taylor（sin（x），2n＋1），sin_min（x，n）=taylor（sin（x），2n），则当x∈对任意 n∈N，sin_max（x，n）＞sin（x）＞sin_min（x，n）；

cos_max（x，n）=taylor（cos（x），2n＋1），cos_min（x，n）=taylor（cos（x），2n），则当对任意 n∈N，cos_max（x，n）＞cos（x）＞cos_min（x，n）；

用f＋和f-分别表示多项式f 展开后的正项和负项之和，显然f=f＋＋f-，并且下面的引理成立：

引理1.2 假设实函数T1（y）＞0，T2（y）＞0 且T1（y）＜x＜T2（y），则

f＋（T1（y），y）＋f-（T2（y），y）＜f（x，y）＜f＋（T2（y），y）＋f-（T1（y），y）.

定理1.1 F（x）=f（x，trans（x）），trans（x）在区间I 可以规范展开，则对任意n∈N，

T_max（n，F）=f＋（x，taylor（trans（x），2n-1））＋f-（x，taylor（trans（x），2n））为 F（x）的上限多项式；

T_min（n，F）=f＋（x，taylor（trans（x），2n））＋f-（x，taylor（trans（x），2n-1））为 F（x）的下限多项式.

定理 1.2 设{T_min（n，F）}和{T_max（n，F）}分别是超越函数多项式 F（x）在区间 I 的下限多项式列和上限多项式列，则在相应区间内，

1）若存在 n0使得 T_min（n0，F）≥0 成立，则 F（x）＞0 成立；

2）若存在 n0使得 T_max（n0，F）≤0 成立，则 F（x）＜0 成立；

3）若存在 n0使得 T_max（n0，F）＞0 和 T_min（n0，F）＜0 都不成立，则 F（x）在区间 I的符号不固定.

上述方案运用Taylor 展开式构造超越函数多项式的上下限多项式列，建立一个逼近目标函数的一元多项式套，从而将目标不等式的证明转化为一系列的一元多项式不等式的验证，我们将这种方案称为Taylor 替换法.

1.2 逐次Taylor替换

一般的超越函数多项式可能包含多个超越因子，超越因子可能还是由超越函数或代数函数复合而成，经过一次Taylor 替换后的函数可能还是包含超越因子，还需要再次甚至多次的Taylor 替换.我们以超越函数多项式F（x）=f（x，trans1（x），trans2（x））和F（x）=f（x，trans1（trans2（x）））为例来描述这个过程：

1、F（x）=f（x，trans1（x），trans2（x）），其中超越函数trans1（x）、trans2（x）在区间I 内可以规范展开，临界值分别为n1、n2.

令f1（x，trans2（x），m）=f＋（x，taylor（trans1（x），2*m），trans2（x））＋f-（x，taylor（trans1（x），2*m-1），trans2（x））；

令f2（x，m，n）=f1＋（x，taylor（trans2（x），2*n），m）＋f1-（x，taylor（trans2（x），2*n-1），m）；

显然当m＞n1时，f1（x，trans2（x），m）＜f（x，trans1（x），trans2（x）），当m→∞时，f1（x，trans2（x），m）→f（x，trans1（x），trans2（x））；

当n＞n2时，对任意m＞n1，f2（x，m，n）＜f1（x，trans2（x），m），当n→∞时，f2（x，m，n）→f1（x，trans2（x），m）；

即当m＞n1，n＞n2时，f2（x，m，n）＜f（x，trans1（x），trans2（x）），当m→∞，n→∞时，f2（x，m，n）→F（x）.

特别地，T_min（n，F）=f2（x，n，n）就是F（x）的下限多项式，{T_min（F，n）}是其下限多项式列，其临界值n0=max{n1，n2}.

类似的方法可以求得F（x）的上限多项式列.

同样的方法我们可以计算含更多“超越因子”形如f（x，trans1（x），trans2（x），trans3（x），…，transm（x））的超越函数的上下限多项式列.

2、F（x）=f（x，trans1（trans2（x））），其中trans2（x）在区间I 可以规范展开，其临界值为n2，trans2（x）在区间I 上的值域为区间J，trans1（x）在J 内可以规范展开，其临界值为n1.

令trans2（x）=u，得到F1（x，u）=f（x，trans1（u）），

令f1（x，m，u）=f＋（x，taylor（trans1（u），2m））＋f-（x，taylor（trans1（u），2m-1）），

显然，当m＞n1时f1（x，m，u）＜F1（x，u）=f（x，trans1（u）），且当m→∞时，f1（x，m，u）→F1（x，u）；

若trans2（x）是代数函数，则f1（x，m，trans2（x））就是F（x）的下限多项式，否则

令f2（x，m，n）=f1＋（x，m，taylor（trans2（x），2n））＋f1-（x，m，taylor（trans2（x），2n-1）），

当n＞n2时，f2（x，m，n）＜f1（x，m，trans2（x））＜F（x）=f（x，trans1（trans2（x））），且当n→∞时，f2（x，m，n）→f1（x，m，trans2（x））；

从而当m→∞，n→∞时，f2（x，m，n）→F（x）=f（x，trans1（trans2（x）））.

特别地，T_min（F，n）=f2（x，n，n）是F（x）的下限多项式，{T_min（F，n）}是其下限多项式列.其临界值n0=max{n1，n2}.

类似的方法可以求得F（x）的上限多项式列.

同样的方法我们可以计算含形如trans1（trans2（trans3（x）））经过更多次复合而成的超越因子的超越函数的上下限多项式列.

我们把上述方案称为逐次Taylor 替换，一个可以计算一般超越函数多项式f（x，trans1（x），…，transn（x））的上下限多项式列的逐次Taylor 替换过程可以递归地定义如下：

算法 1.1 STS（Successive Taylor Substitution）

输入①超越函数多项式F（x）；②n∈N；

输出F（x）的下（上）限多项式.

1）若 F（x）为代数函数

return[F（x），F（x）]；

算法结束；

2）设trans（x）是F（x）的一个超越因子且可以表示为F（x）=f（x，trans（x））

2.1）若trans（x）在相应区间可以规范展开，则

f1（x，n）←f＋（x，taylor（trans（x），2n））＋f-（x，taylor（trans（x），2n-1））；

T_min（n，F）←STS（f1（x，n））[1]；

f2（x，n）←f＋（x，taylor（trans（x），2n-1））＋f-（x，taylor（trans（x），2n））；

T_max（n，F）←STS（f2（x，n））[2]；

return[T_min（n，F），T_max（n，F）]；

2.2）若trans（x）具有形如trans1（trans2（x））的复合形式，令F（x）=f（x，trans1（u）），其中u=trans2（x），假设trans1（u）在相应区间可以规范展开.

f1（x，n，u）←f＋（x，taylor（trans1（u），2n））＋f-（x，taylor（trans1（u），2n-1））；

T_min（n，F）←STS（f1（x，n，trans2（x）））[1]；

f2（x，n，u）←f＋（x，taylor（trans1（u），2n-1））＋f-（x，taylor（trans1（u），2n））；

T_max（n，F）←STS（f2（x，n，trans2（x）））[2]；

return[T_min（n，F），T_max（n，F）]；

3）END.

算法STS 还不能直接处理类似tan（x）、ln（1-x）、ex这类不能规范展开的超越因子，在证明过程中需要结合人工证明和做一些的变量代换.

超越函数多项式的“超越因子”还可能就是超越常数，也需要有理化.本文的处理方法是将超越数视为一个超越函数，构造一个逼近该超越数的有理数端点区间套.比如对于超越数t，我们构造满足如下性质的区间列{[t1（n），t2（n）]}：

1）t1（1）＜t1（2）＜…＜t1（n）＜…＜t＜…t2（n）＜…t2（2）＜t2（1）；

2）当n→∞时，t1（n）→t，t2（n）→t；

3）端点t1（n）和t2（n）均为有理数.

若f（x，t）是系数含超越数t 的一元多项式，则

T_max（n，f）=f＋（x，t1（n））＋f-（x，t2（n））为f（x，t）的上限多项式；

T_min（n，f）=f＋（x，t2（n））＋f-（x，t1（n））为f（x，t）的下限多项式.

输入：n∈N；

输出：有理数端点区间[t1（n），t2（n）]，满足：对任意p≤n，t1（1）＜t1（2）＜…＜t1（p）＜＜t2（p）＜…＜t2（2）＜t2（1）；当n→∞ 时，t1（n）→，t2（n）→.

1）t1←16*subs（x=1/5，arctan_min（x，n））-4*subs（x=1/239，acrtan_max（x，n））；

2）t2←16*subs（x=1/5，acrtan_max（x，n））-4*subs（x=1/239，tarctan_min（x，n））；

3）return[t1，t2]；算法结束.

2 定理2的证明

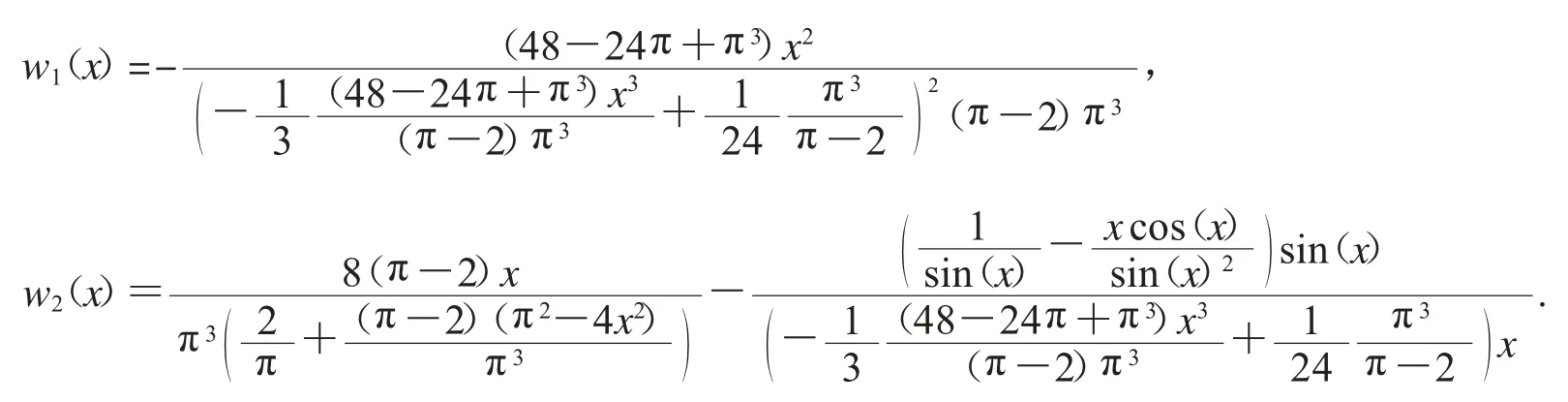
令f3（x）=numer（f2（x））*denom（f2（x））（其中numer（f（x））和denom（f（x））分别取分式的分子和分母，下同），显然sgn（f2（x））=sgn（f3（x））.

令g1（x，n）=subs（ln（x/sin（x））=B（x，n），f3＋）＋subs（ln（x/sin（x））=A（x，n），f3-），则对任意n∈N，g1（x，n）＜f3（x）；

令g2（x，n）=numer（g1（x））*denom（g1（x））；

令g3（x，n）=subs（sin（x）=sin_min（x，n），g2＋）＋subs（sin（x）=sin_max（x，n），g2-），则对任意n∈N，g3（x，n）＜g2（x，n）；

令g4（x，n）=subs（cos（x）=cos_min（x，n），g3＋）＋subs（cos（x）=cos_max（x，n），g3-），则对任意n∈N，g4（x，n）＜g3（x，n），此时g4（x，n）还含有超越数作为系数；

令g5（x，n）=subs（=_to_ra（tn）[1]，g4＋）＋subs（=_to_ra（tn）[2]，g4-），则对任意n∈N，g5（x，n）是关于x 的一元有理多项式，且g5（y，n）＜g4（x，n）＜g3（x，n）＜g2（x，n）；

使用BOTTEMA 的xprove 指令：xprove（g5（x，n）＞0，[x＜_to_rat（n）[2]/3]）， 当n=5 时，不等式g5（x，n）＞0 成立，即当x∈（0，x＜_to_ra（t5）[2]/3）（0/3］，g2（x，5）＞0，从而f3（x）＞g1（x，5）＞0，继而f2（x）＞0，得到f1（x）在（0/3］内单调上升.

证明f1（x）=-ln（u（x））-1/v（x）*ln（x/sin（x）），由于u（0）=1，v（0）=且当x→0＋，ln（x/sin（x））→0，所以当x→0＋，f1（x）→0.而由引理3.1，当x∈（0，/3］，f1（x）关于x单调上升，从而f1（x）＞0.

证明 令w3（x）=nume（rw1（x））*denom（w1（x）），得到

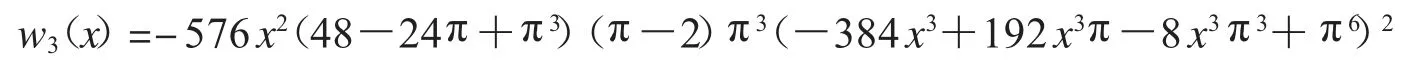
令w4（（x，n）=subs（=_to_ra（tn）[2]，w3＋）＋subs（=_to_ra（tn）[1]，w3-），则w4（x，n）是关于x 的有理多项式，且对任意n∈N，w4（x，n）＞w3（x）；

使用BOTTEMA 的xprove 指令：xprove（w4（x，n）＜0，[x＜_to_ra（tn）[2]/2]），当n=2 时，w4（x，n）＜0 成立，即在（0/2］内0＞w4（x，2）＞w3（x），从而w1（x）＜0.

证明 令f4（x）=-（ln（x/sin（x））＋w2（x）/w1（x）），由引理2.2 知，在（0，/2］内w1（x）＜0，所以在（/3，/2］内sgn（f4（x））=sgn（f2（x））.

令f5（x）=f4（`x），则f5（x）为包含x、sin（x）、cos（x）、的分式.由于 cos（x）在（/3，/2）内不能规范展开，作变量替换x=/2-y，则f5（x）＜0 在（/3，/2）内成立等价于在（0/6）内g（y）=f5（/2-y）＜0 成立.

令g1（y）=numer（g（y））*denom（g（y））；

令g2（y，n）=subs（sin（y）=sin_max（y，n），g1＋）＋subs（sin（y）=sin_min（y，n），g1-），则对任意n∈N，g2（y，n）＞g1（y）；

令g3（y，n）=subs（cos（y）=cos_max（y，n），g2＋）＋subs（cos（y）=cos_min（y，n），g2-），则对任意n∈N，g3（y，n）＞g2（y，n）；

令g4（y，n）=sub（s=_to_ra（tn）[2]，g3＋）＋sub（s=_to_ra（tn）[1]，g3-），则g4（y，n）是关于y 的一元有理多项式，且g4（y，n）＞g3（y，n）＞g2（y，n）＞g1（y）；

使用BOTTEMA 的xprove 指令：xprove（g4（y，n）＜0，[y＜_to_rat（n）[2]/6]）， 当n=8 时，不等式g4（y，n）＜0 成立，即在（0/6）内g1（y）＜0 成立，g（y）＜0 成立.从而在（/3/2）内f5（x）＜0 成立.由此得到f4（x）在（/3/2）内单调下降.

下面讨论f2（/2）的符号.令

h1=nume（rf2（/2））*denom（f2（/2））=其中和ln（/2）需要有理化，令t=/2-1，则 t∈（0，1），ln（1＋t） 可以规范展开，即对任意 n∈N，ln_max（t，n）＞ln（1＋t）=ln（/2）＞ln_min（t，n），令 E（n）=subs（t=/2-1，ln_max（t，n）），F（n）=subs（t=/2-1，ln_min（t，n）），则 E（n）＞ln（/2）＞F（n）.

令h2（n）=subs（ln（/2）=E（n），h1＋）＋subs（ln（/2）=F（n），h1-）；

令h3（n）=subs（=_to_ra（tn）[2]，h2（n）＋）＋subs（=_to_ra（tn）[1]，h2（n）-），则对任意n∈N，h3（n）＞h2（n）＞h1.h3（n）是含n 的有理式且容易得到h3（5）＜0，所以h1＜0，从而f2（/2）＜0.

f2（/2）＜0 就得到f4（/2）＜0 成立.又由引理2.1 知f2（/3）＞0，所以f4（/3）＞0，从而在（/3，/2）内存在唯一x0使得f4（x0）=0，并且在（/3，x0）内f4（x）＞0，从而f2（x）＞0，在（x0，/2）内f4（x）＜0，从而f2（x）＜0.

而f2（x）=f1（`x），所以f1（x）在（/3，x0）内单调上升，在（x0/2）内单调下降.由推论2.1 知f1（/3）＞0，从而f1（x）＞0 在（/3，x0]内成立；而f1（/2）=0，所以f1（x）＞0 在（x0/2）内成立.所以f1（x）＞0 在（/3，/2）内成立.

由推论2.1 和引理2.3 知f1（x）＞0 在（0，/2）内成立，从而 （fx）＞0 在（0，/2）内成立，即定理2 成立.

3 结束语

逐次Taylor 替换是处理超越函数多项式不等式自动证明的有效方案，其主要思路是借助Taylor 展开式建立一个逼近目标函数的多项式套，从而将证明转化为一系列的一元多项式不等式的验证，然后借助BOTTEMA 等代数不等式证明工具完成最后的工作.算法可以处理含多个不同超越因子和复合超越因子的超越函数多项式不等式，在证明过程中若结合人工证明和巧妙的代换方法，更能发挥逐次Taylor 替换算法的效能.

本文解决了一个一类形如sin（x）/x＞u（x）v(x)的幂指函数不等式的机器证明问题，是逐次Taylor 替换成功运用的案例.虽然结论是已知结果，但方法本身对同类不等式具有示范性，能够为文献[1-11]中其它幂指函数不等式（或幂函数不等式）的机器提供证明方案.