基于回声状态网络的炼油厂氢气网络动态用氢成本预测及应用

左春玲， 张正明， 曹萃文

(华东理工大学 化工过程先进控制和优化技术教育部重点实验室，上海 200237)

近年来，随着炼油产品的升级和原油的重质化、劣质化，石油化工企业对氢气资源的需求迅速增加，炼油企业催化重整装置的副产氢气已经满足不了生产需要，需采取增加制氢装置、扩大已有装置制氢能力、从外界购买新氢、优化氢气网络等多项措施来弥补不足。氢气从产出到被下游装置使用，如何合理地安排好产、耗平衡，直接涉及到炼油厂整体的平稳生产和经济效益。

已有的对氢气优化利用的研究，主要为夹点分析法[1-3]和超结构法[4-9]。夹点分析法是对现有装置的氢气纯度、压力、流量、杂质含量等约束条件进行分析[10]，主要以公用工程最小用量[2]或最小新氢供应量[3]为目标，通过绘制氢负荷流量图等来确定夹点位置。该方法易于实际工程操作和执行，方便确定网络整体用氢目标，但不适合进行整个系统的动态经济效益指标分析。

超结构法[4]简化了装置，注重各装置之间的关系，将产氢、耗氢装置分别作为氢源、氢阱，建立了包括所有可能有连接关系的网络超结构。这种连接关系考虑实际生产过程中的各种约束条件，如：物料守恒、浓度守恒、压力条件和设备配置等，用数学规划法求解，满足所有约束条件并使目标函数最优。在优化炼油厂的氢气网络时，通常以静态成本最小为目标[8,10]，可以综合考虑操作费用和设备投资费用。2012年，Liao等[8]提出了一种适用于氢气网络改造设计的方法，通过建立状态空间超结构模型获得了更多的网络结构，权衡了各种静态操作成本和投资成本。曹萃文等[9]发明了一种在超结构法中混合夹点约束的炼油厂氢气网络优化调度方法，其中的成本目标仍然是静态成本。康永波[11]提出以供氢成本和新制氢气剩余量为目标的氢气网络多目标模型，在氢耗需求不确定环境下，建立鲁棒优化模型，利用遗传算法求解，并与普通优化比较，证明了在氢气网络优化过程中充分考虑不确定参数变化的重要性。

氢气网络是复杂的非线性系统，对复杂系统进行研究主要是建立系统的差分方程模型或者微分方程模型，根据数学模型的特点来探索系统的动力学机制。然而，在实际问题中，由于系统结构复杂，参数随时间变化，通常无法获得完备的和确定性的信息，很难建立精确的解析模型。在此情况下，可以运用数据驱动技术研究系统的动态行为。该技术对系统内在的背景知识需求较少，对模型机理要求较少，为那些无法建立精确解析模型的实际系统提供了一条新的研究途径。2004年，Jaeger提出了回声状态网络(Echo state network，ESN)，并对混沌时间序列进行预测，通过实验证明回声状态网络的预测精度比之前报道的预测结果提高了2400倍[12]。回声状态网络因为其训练简单和建模精度高等优点，广泛应用于时间序列预测[12-13]、非线性系统识别[14]、图像处理[15]、自然语言识别[16]、电力负荷预测[17]等领域，针对不同应用领域对回声状态网络的优化改进算法研究也越来越多。田中大等[18]将一种基于贝叶斯回归的回声状态网络应用于小型水电站的短期电力预测，克服了传统神经网络中存在的病态解降低模型泛化能力的缺陷。Deihimi等[19]提出一种多层的回声状态网络结构，用于预测特定时刻的电力负荷。模型可预测一天24 h每个整点时刻的电力负荷，使预测结果更加精准且符合实际应用的要求。王莉莉[20]针对污水处理过程的非线性、大时变等特点，提出一种基于回声状态网络的多变量自适应预测控制策略，实现了优化控制。刘颖等[21]通过奇异值分解求取ESN储备池到输出层的权值对ESN进行改进，改进后的ESN已应用于高炉煤气发生量的预测中。盛春阳等[22]提出一种基于滤波过程改进回声状态网络的时间序列预测方法，采用滤波过程来估计回声状态网络储备池神经元的状态和网络输出权值，能避免参数求解过程中常出现的异常解问题，有效预测冶金企业氧气系统的氧气流量。

笔者以某炼油厂实际焦化干气水蒸气制氢装置产氢量的动态变化数据为基础，通过“基于LabVIEW的氢气网络优化调度软件V 1.0”[23]计算得到的动态成本数据，详细分析了某炼油厂氢气网络成本特点，首次提出采用预测精度较高的回声状态网络对氢气网络动态成本进行数据驱动建模及预测，然后根据预测出的成本在不同工况下最低供氢成本的优化操作区域中的位置，对氢气网络的合理配置提供决策支持。

1 回声状态网络

1.1 回声状态网络模型

经典的回声状态网络是一种三层递归神经结构[13,19]，包括K个神经元组成的输入层、N个神经元组成的隐含层(储备池)和L个神经元组成的输出层，如图1所示。隐含层又称储备池，含有成百上千个稀疏递归连接的神经元，与递归神经网络中的隐含层对应。

ESN状态方程：

x(t)=f(Winu(t)+Wx(t-1)+Wbacky(t-1))

(1)

ESN输出方程：

y(t)=fout(WoutX(t))

(2)

公式(1)和(2)中：x(t)∈RN×1、x(t-1)∈RN×1(R为实数集合)分别为t时刻、t-1时刻储备池内部状态；u(t)∈RK×1是离散时刻t时的外部输入；Win∈RN×K为输入连接权值矩阵；W∈RN×N为储备池内部神经元连接权值矩阵(一般保持[1%,5%]的稀疏连接)，Win和W均随机初始化并且保持固定不变；Wback∈RN×L为输出反馈矩阵(目的是将上一时刻网络输出反馈到当前时刻状态中；X(t)≡[x(t)T,u(t)T]T；Wout∈RL×(N+K)是输出连接权值矩阵；y(t)∈RL×1、y(t-1)∈RL×1分别是离散时刻t、t-1时对应的ESN输出。f(·)表示储备池神经元激活函数，通常取非线性函数，如双曲正切函数或sigmoid函数；fout(·)表示输出层神经元激活函数，通常取线性函数，对于高度非线性的对象，也可选用非线性函数。

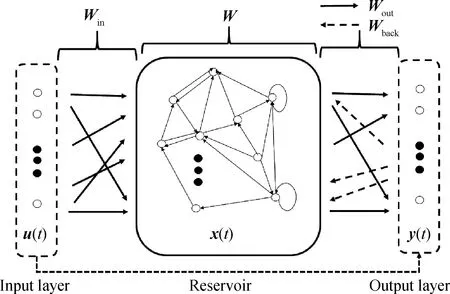
图1 标准ESN的结构示意图Fig.1 Structure of standard ESN

储备池是回声状态网络的核心结构，其参数对回声状态网络的性能好坏有很大的影响。根据不同时间序列的特点，设计适合的储备池结构是回声状态网络建模的首要问题。储备池主要参数[15,18]包括激活函数类型、储备池的规模、内部连接矩阵的谱半径、稀疏度以及输入变换系数。

1.2 回声状态网络的训练与测试

首先根据实际样本数据来确定回声状态网络的规模和参数，再进行网络的训练和测试。回声状态网络的训练过程就是根据给定的训练样本u(t)、y(t)(t=1,2,…,r)确定系统中的输出连接权矩阵Wout的过程。一般假定Wback=0。ESN的训练过程可以分为2个阶段：采样阶段和权值计算阶段。

1.2.1 采样阶段

采样阶段是首先任意选定网络初始状态，但是通常情况下令x(0)=0。训练样本u(t)(t=1,2,…,m,…,r)经过输入连接权矩阵Win，y(t)经过反馈连接权矩阵Wback分别被加入到储备池。按照公式(1)状态更新方程，依次完成系统状态的计算。

为了计算输出连接权值矩阵Wout，需要从某一时刻m开始收集储备池状态变量x(t)和输入变量u(t)，并以向量[xT(t),uT(t)]=[x1(t),x2(t),…,xN(t),u1(t),u2(t),…,uK(t)](t=m,m+1,…,r)为行构成矩阵H(M-m+1,N+K)，其中M是训练样本的数量；同时相应的目标输出y(t)也被收集，以yT(t)=[y1(t),y2(t),…,yL(t)](t=m,m+1,…,r)为行构成矩阵Z(M-m+1,L)。

1.2.2 权值计算

(3)

(4)

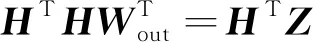
Wout=((HTH)-1HTZ)T

(5)

2 基于回声状态网络的氢气网络动态用氢成本预测

炼油企业各类产品的生产均随市场需求和炼油厂实时工况的变化而变化，因此，对氢气网络因产氢量和耗氢量变化以及不同工况导致的氢源(产氢装置)、氢阱(耗氢装置)不同配置下的实时动态用氢成本进行准确的预测，能够对氢气网络的合理配置与优化提供决策支持。ESN的储备池神经元连接方式复杂，能够与其他神经元随机连接，也可以自连接，相比于BP、KNN等及其他递归神经网络，可以实现复杂系统的高精度建模。

2.1 数据来源及其处理

笔者对国内某大型炼油厂生产过程进行了调研，该炼油厂常规使用的供氢装置有外购纯氢(氢源1)、2套水蒸汽制氢装置(氢源2)、2套乙烯装置附产氢(氢源3)、3套重整装置附产氢(氢源4)、2套裂解汽油加氢装置附产氢(氢源5)、1套柴油加氢装置附产氢(氢源6)、1套催化汽油脱硫装置附产氢(氢源7)、1套高压加氢裂化装置附产氢(氢源8)、2套歧化装置附产氢(氢源9)和2套异构化装置附产氢(氢源10)，其某月的氢源数据平均值见表1[11]。该炼油厂耗氢装置有3套裂解汽油加氢装置(氢阱1)，3套柴油加氢装置(氢阱2)，1套催化汽油脱硫装置(氢阱3)，1套中压加氢裂化装置(氢阱4)，1套高压加氢裂化装置(氢阱5)，1套航煤临氢脱硫醇装置和石脑油预加氢装置(氢阱6)，1个涤纶部用氢(氢阱7)，1套渣油加氢装置、塑料部用氢和硫磺装置(氢阱8)，2套歧化装置(氢阱9)，2套异构化装置(氢阱10)，其同月的氢阱数据平均值见表2[11]。(表1和表2中的数据，是排除地理位置因素，将相同氢气纯度的装置归为了同一个等级后的结果。)

表1 某炼油厂的氢源数据Table 1 Hydrogen sources data of the refinery

1) Normal state

笔者在“基于LabVIEW的氢气网络优化调度软件V 1.0”[23]中运用了文献[11]的超结构线性规划数学模型，列出如下：

(1)模型约束

式(6)为氢源流量约束，表明氢源j分配到所有氢阱k的氢气流量不大于氢源j的供气流量，且供应流量必须不大于氢源j的最大设计供应量。

(6)

表2 某炼油厂的氢阱数据Table 2 Hydrogen sinks data of the refinery

1) Normal state

(7)

式(8)为氢气浓度约束。该式表明各氢源j流入氢阱k的氢气纯度必须不小于氢阱k的氢气纯度要求。

(8)

其中，ωj为氢源j的氢气纯度，%；ωk为氢阱k要求的氢气纯度，%。

(2)目标函数：

超结构模型的目标函数可以设为多种形式，笔者为考察炼油厂氢气网络的动态用氢成本，列目标函数如式(9)所示。

(9)

其中，TH2为单位时间H2网络的耗氢总成本，CNY/h；cj为氢源j的H2价格，CNY/m3。

常规研究一般只针对表1和表2中的H2网络各装置产氢和耗氢数据，代入超结构模型进行求解后得到一个固定的网络用氢成本或其他目标，无法反映实际生产的动态环境对目标的影响。为改善这种情况，笔者以该炼油厂焦化干气水蒸气制氢装置(氢源2)为例，采集了装置的实际产氢数据，并在Aspen HYSYS软件中模拟该装置的生产过程，在软件的各项输出数据与实际数据吻合后，扩展主要操作参数变动值为各类不同工况下的极限值，得到4100组氢源2的产氢数据。图2为对应的不同压缩机出口压力和原料气中水/碳摩尔比条件下的氢源2的产氢量。在笔者开发的应用软件[23]中，对每一组数据采用单纯型算法求解氢气网络线性规划模型得到全局最优解，即得到在氢源2产氢量动态变化下的4100组成本和相应的氢气网络配置结构。最后将所有影响产氢量的参数配置数据、氢气流量和纯度数据、成本优化结果都通过LabVIEW软件自动存入MySQL数据库中。图3为通过不同压缩机出口压力和原料气中水/碳摩尔比条件下的最小用氢成本。

图2 不同压缩机出口压力和原料气水/碳摩尔比条件下的氢源2产氢量Fig.2 Hydrogen production of hydrogen source 2 underdifferent compressor outlet pressure andfeedstock water/carbon molar ratios

2.2 氢气网络动态成本预测

由2.1节的数据处理过程可以看到，随着氢源2的产氢量变化(实际上所有氢源、氢阱的产氢量和耗氢量及相关指标均可能发生变化)，氢气网络的实时动态用氢成本并不容易实时在线得到，因此避开氢气网络中各装置机理模型在Aspen HYSYS软件中的复杂仿真过程，开展根据各临氢装置主要操作参数变化导致的氢气网络成本变化的数据驱动建模及实时预测，对提高炼油厂的操作优化水平、降低氢气使用成本具有很好的指导意义。

在焦化干气水蒸气制氢装置(氢源2)的生产过程中，原料气的流量、水/碳摩尔比、烯烃含量、硫含量、催化剂活性、反应器温度和压力的改变都会影响氢气产量，但在实际生产中，影响产氢量最大的常规操作参数为原料气的水/碳摩尔比和压缩机出口压力数据(压缩机位于第一级主反应器入口处)。

图3 最小用氢成本与水/碳摩尔比和压缩机出口压力的关系Fig.3 Relationship between minimum hydrogen cost,water/carbon molar ratio and compressor outlet pressure(b) is vertical view of (a)

下面以4100组氢气网络的动态用氢成本数据为例，说明训练回声状态网络，从而预测氢气网络的最新动态用氢成本的过程。

焦化干气水蒸气制氢装置的原料气水/碳摩尔比和压缩机出口压力为回声状态网络的二维输入，所对应的最小用氢成本作为目标输出。4100组数据分为两部分，3000组为网络训练数据集，1100组为网络测试数据集。回声状态网络的性能通过使用公式(10)的归一化均方根误差(Normalized root mean square error，e)来评估[12]。

(10)

储备池内部取1500个神经元(根据多次改变储备池内部神经元个数的实验结果比较，N=1500能有更好的预测效果)，稀疏连接为2%，随机生成输入连接矩阵Win和储备池内部连接矩阵W并保持不变，谱半径是储备池内部连接权矩阵W的最大特征值的绝对值。运用训练数据集和任意网络的初始状态(令x(0)=0)进行储备池状态的更新计算，最后求解网络输出值，可以得到如图4、图5、图6所示的结果。因储备池内部的神经元个数较多，图4显示的是储备池内部任意选取的4个神经元的前200个状态变量值(x1(t),x2(t),x3(t),x4(t),t=1,2,…,200)，被收集在矩阵H中；不同的输入变量在状态更新方程(见公式(1))计算后产生不同的状态变量x(t)。图5为在某一次独立运行时3000组训练数据目标期望值与回声状态网络预测输出值的对比图。图6为1100组测试数据目标期望值与回声状态网络预测输出值的对比图。由图5和图6可以看出，在假设其他条件都不变的情况下，回声状态网络可以很好地根据压缩机出口压力和原料气水/碳摩尔比来预测氢气网络的最小用氢成本。

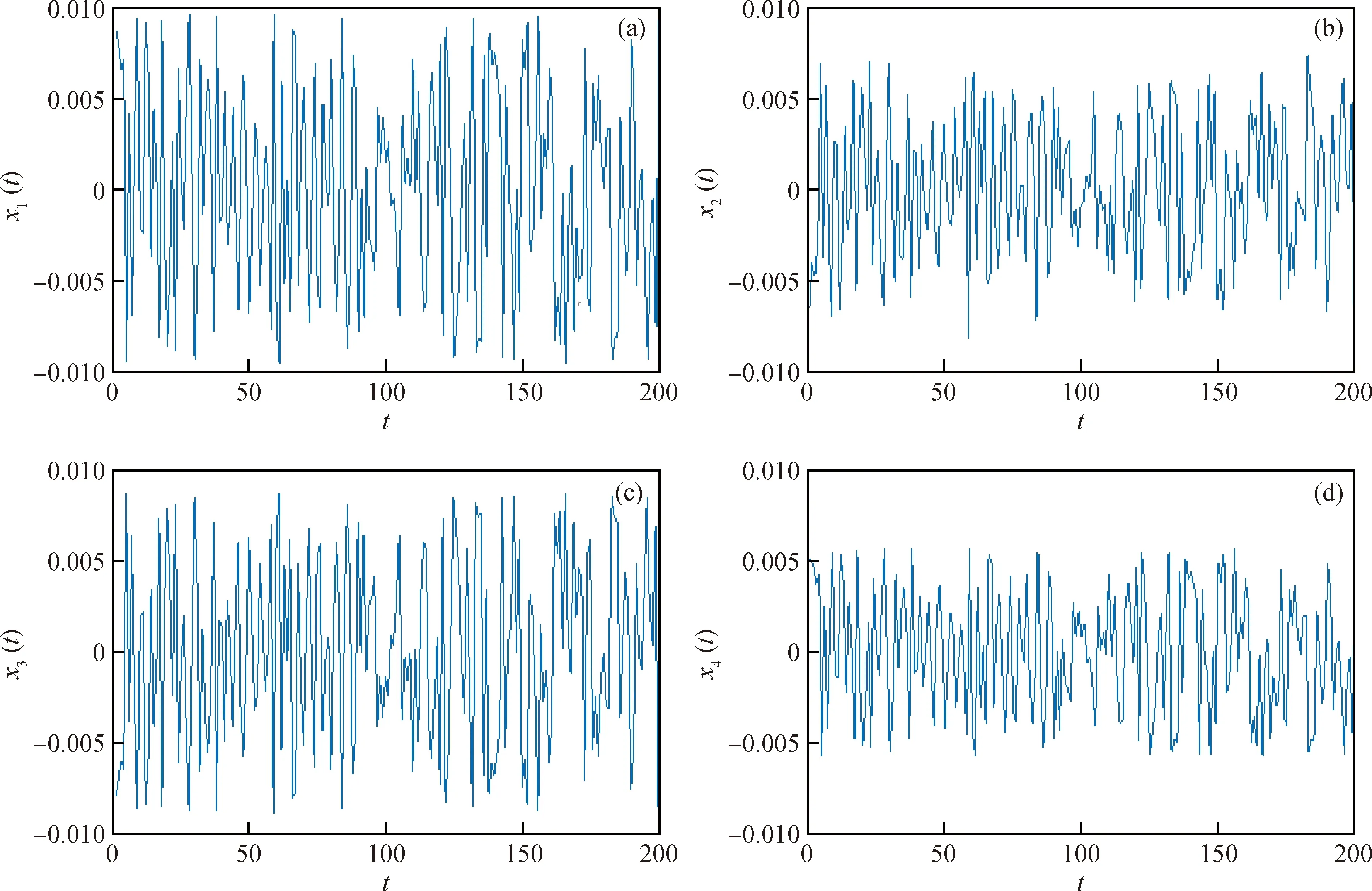
图4 选取的4个储备池内部神经元的前200个状态变量值Fig.4 The front 200 state variable values for neurons in the four selected reserve pools(a) X1(t); (b) X2(t); (c) X3(t); (d) X4(t)

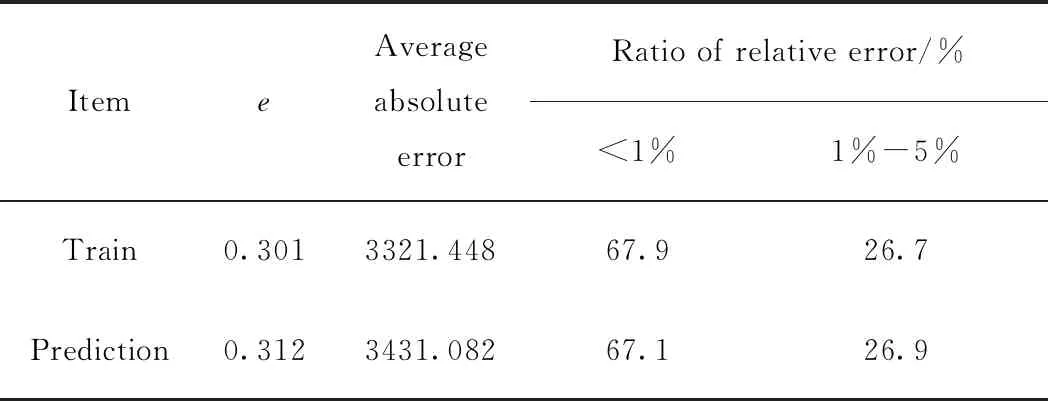
表3为回声状态网络在氢气网络动态成本预测中的性能指标。性能评估指标为归一化均方根误差、平均绝对误差、相对误差小于1%、1%～5%和大于5%的样本比例，结果是独立运行50次计算得到的平均值。由表3可以看出，多于95%的数据可以达到预测相对误差小于5%。这足以区分该条件下的最小用氢成本所在的范围，并为最终能寻找到最优氢气网络结构和操作条件提供数据支撑。

3 基于氢气网络动态用氢成本预测值的区块操作优化

3.1 区块划分分析

为将第2.2节中预测出的实时网络用氢成本数据用于指导运行操作，笔者对氢源2的2个典型操作参数(原料气的水/碳摩尔比和压缩机出口压力)变化时产生的4100组用氢成本数据进行了分析。由图3 可知，最小用氢成本与2个典型参数之间的关系是非线性的，可以以压力2840 kPa为分界点将其划分为12个区块：图7(a)显示了压力小于等于2840 kPa时最小供氢装置成本与水/碳摩尔比和压缩机出口压力的关系(6个区块)；图7(b)显示了压力大于等于2840 kPa时最小供氢装置成本与水/碳摩尔比和压缩机出口压力的关系(6个区块)。

3.2 在区块跳跃处的操作优化分析

当最小用氢成本出现区块间跳跃时(如图7所示不同颜色的区块)，说明该最小用氢成本对应的氢气网络中氢源、氢阱的氢气流量分配发生了改变。随机选取其中一个跳跃的相邻部分，如图7(a)圆圈圈出来红色区域和绿色区域的两点。红色区域上的圆圈(压力为2790 kPa、水/碳摩尔比为3.126)，此时各氢源分配到各氢阱之间的氢气流量如表4所示，最小用氢成本为287851.70 CNY/h；绿色区域上的圆圈(压力为2790 kPa、水/碳摩尔比为3.165)，此时各氢源分配到各氢阱之间的氢气流量如表5所示，此时的最小用氢成本为255635.49 CNY/h。从表4和表5可以看出，由于水/碳摩尔比(即操作方式)的微小变化，导致氢气网络中氢源4、氢源5和氢源8对氢阱1、氢阱2、氢阱3和氢阱4的供氢网络结构和氢气流量发生改变，以至于最小用氢成本减少32216.21 CNY/h。因此，当第2.2节中预测的最新网络用氢成本数据处在区块的边界处时，对应的操作参数应向成本较小的下区块对应值处调整。

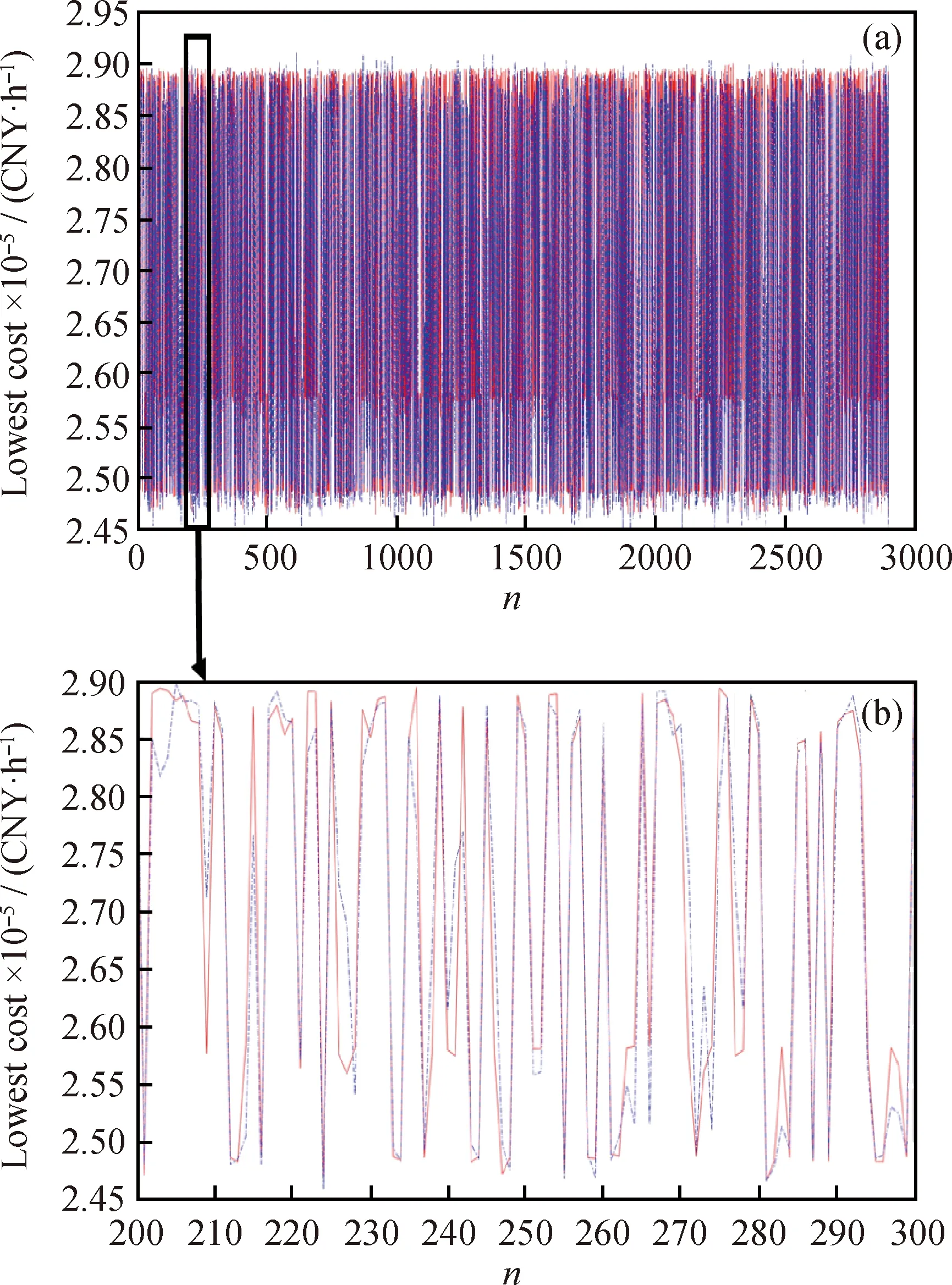
图5 训练数据的期望输出值和ESN输出值Fig.5 Expected value and ESN output value of training data(a) All of the training data； (b) Part of the training data Teacher sequence; Predicted sequence

图6 测试数据集的期望值和ESN输出值Fig.6 Expected values and ESN output values of test data(a) All of the test data； (b) Part of the test data Teacher sequence; Predicted sequence

ItemeAverageabsoluteerrorRatio of relative error/%<1%1%-5%Train0.3013321.44867.926.7Prediction0.3123431.08267.126.9

3.3 在同一区块上的操作优化分析

由图7可知，在一定的水/碳摩尔比和压缩机出口压力范围内(图7(a)和图7(b)中相同颜色区域，即同一区块上)，氢气网络结构不会发生频繁的变动，体现了实际可操作性。即：如果第2.2节中预测的网络最新用氢成本值在某一区块中时，可以根据实际情况调节水/碳摩尔比或压力到同一区块的最小用氢成本时的条件。图7中三角形标出的点即为每个不同区块的最小用氢成本值。如:当实际需要水/碳摩尔比范围在3.946～5.079、压力范围在2840～3270 kPa时(图7(b)中最下方深蓝色区域)，操作调节水/碳摩尔比为4.063和压力为3010 kPa，则可以在不改变氢气网络结构的前提下，获得最小用氢成本为 248250.00 CNY/h。

表4 氢源-氢阱之间的氢气流量分配(图7(a)红色区域的圆圈)Table 4 Flow distribution of hydrogen between hydrogen sources and sinks (Circle in the red region of Fig.7(a)) QH2/(m3·h-1)

The flow rate distributions of Hydrogen source 3, Hydrogen source 7, Hydrogen source 9, Hydrogen source 10 and Hydrogen sink7, Hydrogen sink 8, Hydrogen sink 9, Hydrogen sink10 are all 0, so they are not listed in the table.

图7 最小用氢成本与水/碳摩尔比和压缩机出口压力的关系Fig.7 Relationship between the minimum hydrogen cost, the water/carbon molar ratio and compressor outlet pressure(a) p≤2840 kPa; (b) p≥2840 kPaTriangles mark the state, in which each block costs the least. Circles are examples of optimization operations.

QH2/(m3·h-1)

Same legend as in Table 4.

4 结 论

(1)在利用某炼油厂氢气网络实际数据和Aspen HYSYS流程模拟获得的数据集合基础上，分析了氢气网络最小用氢成本和相应的氢气网络流量分配变化的情况。

(2)以该炼油厂氢气网络中水蒸汽制氢装置的原料气水/碳摩尔比和压缩机出口压力数据变化对最小用氢成本的影响为例，说明了运用回声状态网络对氢气网络最小用氢成本进行预测的可操作性，超过95%预测结果的相对误差小于5%。

(3)由于最低用氢成本与2个主要操作参数(原料气的水/碳摩尔比和压缩机出口压力)之间存在非线性关系，对其进行了区块操作优化划分分析。结果表明：可以根据预测的最小用氢成本在不同区块上的位置，在对应实际生产条件范围内寻找到最低用氢成本时的最优操作参数设置；也可以根据预测的最小用氢成本在同一区块上的位置，在对应实际生产条件范围内寻找到最低用氢成本时的最优操作参数设置。