高中数学课堂教学精细化组织的几点思考

甘肃省合水县第一中学 潘应平

在高中数学课堂中利用精细化教学，以提升课堂教学效率的方式有许多途径。本文主要从以下三个方面展开思考：细化环节，以提升课堂效率；细化目标，以明确学习中的重难点内容；细化问题与思路，以实现学生生成发散性思维，最终实现利用精细化细节帮助学生掌握数学知识、形成数学思维。

一、细化环节，提升课堂效率

数学知识的教学往往比较抽象，并且对数学知识的理解经常是学生的不足之处，想要在先天条件不佳的情况下来提升数学课堂的教学效率，教师首先应该在贴合教材的基础上，将数学内容不断精细化，直至易于被学生理解和接受，当学生对每一个细化的内容都掌握之后，再将这些知识串联起来。

例如在学习“函数概念”这节内容时，教师可以在教学环节上入手，对教学环节展开精细化教育。通常教师在进行环节设计时会将课堂环节划分为三个板块：实例展示（三至四个)、发现共同点、总结分析并引出概念。这样的设计从教学目标与教学模式的角度来看，是非常正常并通用的一种方式，但是其运用在实际教学过程中往往达不到预期的效果。这是因为仅仅利用几个例子的展示就要求学生分析出其中的共性是非常困难的，这样的教学环节设计太粗略，以至于学生跟不上教师的思维步伐。因此，教师应该将教学环节精细化地划分为以下四个步骤：感受时间流逝产生变量概念、研究变量规律建立关系、分析关系共性产生变量形式、统一形式引出变量定义，利用这四个步骤，使学生根据教师设计的教学环节循序渐进地掌握数学知识。函数的核心部分就是掌握变量的性质，学生虽对变量有一定的初步认识，但不够深入，这样的教学环节的设计是为了让学生通过变量这一概念，深入探究函数的概念，由一个熟悉的知识引出一个陌生的知识，也便于学生理解与接受。

对教学环节的精细化设计，是选取适应于学生接受能力和理解能力范围的教学模式，让学生通过步步深入细化的教学基石，了解到更深层面的数学知识，教师在设计教学环节时应该注重环节中学生的反应，适时进行调节和修改，以实现课堂效率的提升。

二、细化目标，明确教学活动中的重难点

教学目标通常是教师在课前进行规划制定，由教师传递给学生的，但实际上目标应该是双向的，不仅教师要完成本节课的教学目标，学生也应该拥有一个具体的学习目标，教师应该帮助学生将学习目标进行细化，见微知著，最终实现师生之间的共同目标。

例如在学习“函数单调性”这一节内容时，纵观这节内容的重难点，主要是教会学生运用多个角度与纬度的数学模型来对“函数单调性的定义”进行表述和界定，并在思维中产生具体的单调性概念模型，在遇到判断函数单调性的问题时能够灵活运用所学知识进行求解。在制定了具体的目标之后，在教学过程中就可以根据目标展开教学活动，并且在教学活动中应思考如何对本节内容的重难点进行精细化分，目标中提到的数学语言又可以分为图形、文字、符号这三个方面，图形和文字对于高中生而言是能够轻松掌握并熟练运用的，那么难点就落在符号这一点上，教学目标即为教导学生运用数学符号进行函数单调性定义的界定。函数单调性把函数分为单调递增函数与单调递减函数，用文字表达则为在函数的定义域内存在a ＜b，仍有f（a)的值恒小于f（b)，那么这个函数为单调递增函数，反之则为单调递减函数；利用图像进行表达是在平面直角坐标系中，函数图像中的每一点的切线的斜率都大于零，则称函数为单调递增函数，反之为单调递减函数；利用符号进行表示则为若函数F（x)为可导函数，若其导函数f（x)≥0，那么函数F（x)为单调递增函数，反之则为单调递减函数。

这种将教学目标与学习目标进行细化的方式，能够确立出教学过程中的重难点内容，并且对重难点内容进行细化分析，让学生能够更加轻松地把握数学知识，丰富自身的数学内涵，并且细化后的内容通常是比较基础的数学知识，这样的方式能够在帮助学生巩固知识的基础上，实现知识的延展与运用。

三、细化问题与思路，培育学生发散思维

细化问题的作用是通过将问题的精细化，让学生对问题产生深刻的印象，以便于在今后的学习中能够触类旁通地解决一系列相似问题。细化思路的作用是通过将解题思路的精细化，弥补学生在解题过程中由于某个知识点的欠缺而导致思路中的漏洞，进而培育出学生的发散性思维。

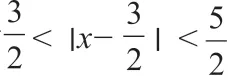
这是一个比较简单的不等式问题，在数学习题中还有许多例题具有一题多解的性质，教师在教学活动中将习题进行精细化的讲解，可以帮助学生从多角度分析问题，掌握多种解题思路，并在今后的自我学习过程中能够自主拓展，形成发散性的思维模式。

总而言之，高中数学教育的最终目标是培育学生的分析与理解能力，解决与操作实际问题能力，并对生活中的事物产生数学性的思维逻辑。为了培养这些能力，教师应该做到从细节出发，将教学活动与教学内容充分展开精细化教育，以细节为基石提升课堂效率，进而实现教育的最终目标。