结合图像，高效学习——初中数学数形结合思想的解题应用

江苏省邗江中学北区校维扬中学 徐 亮

数学是一门严谨的学科，其专业的指导思想决定了数学研究的方法，其中，数形结合思想在研究数学中的数量关系和空间形态上起着非常重要的作用，其指导学生将抽象问题借助图形等，将复杂问题转换成简单问题。但是实际教学中，学生虽然知道有数形结合思想，但是却不能够巧妙运用其分析解决问题，因此，教师要突出数形结合在数学中的应用，加强学生运用数形结合方法解决问题的训练。

一、数形结合在公式证明中的应用

数学解题中最常见的思想就是数形结合，其广泛应用在公式证明上。与其他数学思想相比，数形结合的思想利用直观的图像构建数量关系，方便学生从题目中获取信息，作出与解题有关的辅助线，从而得出相应的结论。由此可见，数形结合的思想在提高学生的学习质量和解题效率上有着非常重要的作用。

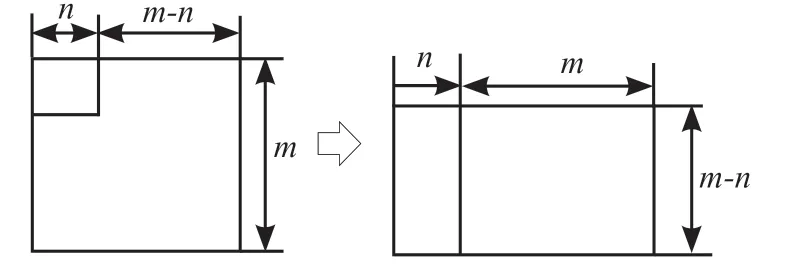
比如初中数学教材中的平方差公式的证明，其运用的面积法就是数形结合方法的具体体现。为了便于学生更加直观地观察，教师在用面积法验证平方差公式时，可以让学生先拿出任意边长的正方形纸张，这里假定边长为m，然后沿着其中一角，剪掉一个边长为n的小正方形，这样就有两个边是m-n，接着再将其中一个突出的图形沿着宽为n 的部分剪开，并将其和长为m，宽为m-n 的部分拼在一起组成一个长方形，最后可以根据图形拼接得到面积等式：m2-n2＝（m+n）（mn），这样就证明了平方差公式。

二、数形结合在函数问题上的应用

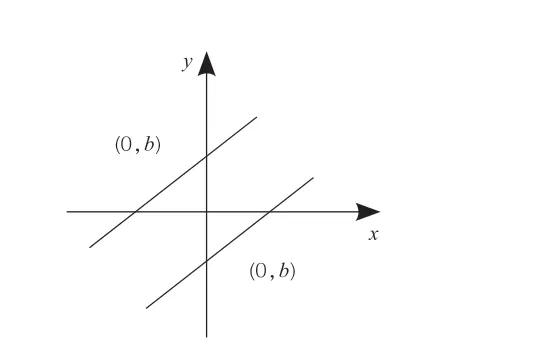
一般初中的函数题除了使用待定系数法，数形结合法也是非常常见的方法，比如学生经常遇到的给点坐标求面积，或者是已知面积求点坐标问题，都是以基本公式思想为依托。一般与函数相关的问题，题目本身是没有图的，如果学生不能照着题干画出大致图像，干想是想不出的，而且一些涉及函数待定系数的问题，学生只有通过画图才能知道函数的大致性质，需要对哪些量进行分类讨论。比如一次函数的k 和b，二次函数的开口方向、对称轴的位置、解的个数，这些只有通过直观形象的图像才能保证解题的完整性。

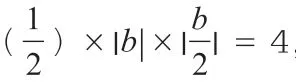
三、数形结合在证明几何问题中的应用

数形结合法除了能够用于公式证明和解函数相关的问题，在几何证明上面也运用得很多。初中涉及的证明题大多都是与三角形有关的，需要学生去添加辅助线，基本上辅助线作对了，证明就没有什么问题了，因此，在线段相等、角相等这些方面，教师要引导学生多作三角形的中线、角平分线、高去构造三角形，然后再利用全等、相似的性质证明线段与线段、角与角之间的关系。

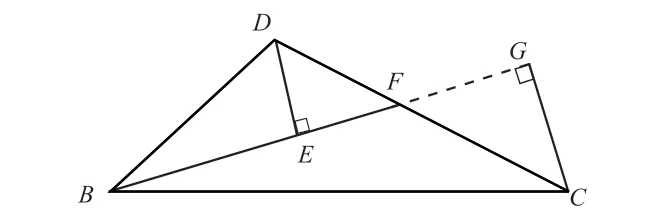
比如：“BF 是△BCD 的中线，DE ⊥BF 于E，CG ⊥BF 交BF的延长线于G，求证：CG ＝DE”，这是典型的用数学结合方法中的面积法证线段相等的题型，而且从题意来看，必然要作辅助线构造出三角形，因为面积法大多就是利用三角形的面积关系来求解。

四、数形结合在概率统计问题中的应用

初中教材中，概率统计部分也涉及数形结合思想，正如我们正常看到的一些简单的随机事件都可以用树状图、折线图、折线图进行分析，还有比较常见的与阴影部分面积有关的概率题。比如：“边长为a 的正方形里面有一个半径为b 的圆形阴影，现在往这个正方形里投石子，那么石子落在阴影部分的概率是多少？”这是一道典型的数形结合的概率题，学生通过画图就能知道概率是

数形结合思想还可以解决与实际生活相关的问题，比如用来判断一场比赛是否公平：“A、B 两个同学在墙上画出半径为20cm 和40cm 的同心圆，然后在与墙相距相同距离处扔同样数量的飞镖，投到小圆内就判定为A 胜，投到大圆里就是B 胜，忽略刚好在两条线上的，没投中的不作数，现在判断游戏是否公平？”学生比较A、B两人投中的概率，得出结论是不公平。

此外，日常中经常遇到求解不规则图形的面积问题，也离不开数形结合和概率的思想，教师可以让学生依葫芦画瓢，仿照之前利用面积法求概率的题型，假定把要求的不规则图形面积圈出来，在其外面或者是里面找出一个规则图形，仿照题目中经常让求石子、飞镖等投进规定区域的概率的思想，学生可以自己往划定的区域去投硬币，记录投到不规则图形里面的次数，然后与总次数相比，得出一个概率值，这个概率值与面积有关，自然就能得到不规则图形的面积。

总之，数形结合思想是初中数学教学中比较重要的思想之一，教师要认真备课进行归纳总结，提高学生的学习兴趣，培养学生数形结合的意识，开拓学生的思维能力，从而全面提高学生的数学综合素质。