《三角形的中位线》的教学设计

江苏省靖江外国语学校初中部 徐忠仪

一、教材分析

1.教材所处的地位和作用

本节课是新苏科版《数学》八年级下册9.5 节内容。它是对前面平行四边形以及矩形、菱形、正方形知识的延伸。教材在探索中位线性质的过程体现了转化的数学思想。

2.教学重点与难点

重点：三角形中位线定理及其应用。

难点：探索三角形的中位线定理。

二、教育教学目标

根据数学课程标准，结合教材内容和学生现状，我制定了以下教育教学目标：

1.理解三角形中位线的概念、性质，并会用它解决有关问题。

2.经历探索三角形中位线性质的过程，体会转化的思想方法，在引导学生应用新知识的过程中，进一步发展学生的思维能力。

3.让学生经历探索三角形中位线性质的过程，丰富学生的数学活动经验，培养学生积极的情感态度。

三、教法、学法

教学过程也是学生的认识过程，没有学生参与的教学活动几乎是无效或低效的教学活动。根据初中学生的生理特点，在教学中，我准备让他们在动手实践以及多媒体的动态观察中探索新知。

教法：通过“操作——观察——探索——验证”的教学过程，运用多媒体及学生动手操作等辅助手段，积极引导学生去观察、思考，获取知识，解决问题，激发学生学习兴趣，让学生在和谐的气氛中掌握知识。

学法：让学生掌握操作与观察、分析与比较、概括与归纳、巩固与提高等科学的学习方法；学会举一反三、灵活转换的学习方法，学会运用转化的思想去解决问题。

四、教学过程

1.情境创设，兴趣导学

星期天，妈妈和小明到公园里游玩，妈妈想考考小明，妈妈指着身旁的跷跷板问小明：“如果跷跷板的支架高50cm，我最多能把你翘起多高？”妈妈又指着跷跷板旁的果树问道：“（如图1）如果果树上有一果子离地面2m，我用跷跷板把你翘起去摘这个果子，那跷跷板的支架高至少为多少呢？（假设跷跷板足够长）”如果你是小明，你能回答这个问题吗？

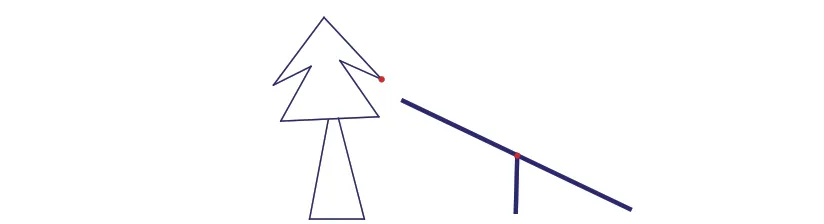
图1

在教学中，学生可能会用全等三角形的知识去解决（如图2），老师进一步提问：假如我们把地平线画出来（如图3），那支架的高与跷跷板翘到的最大高度之间又有怎样的联系呢？这就是我们今天要研究的问题。

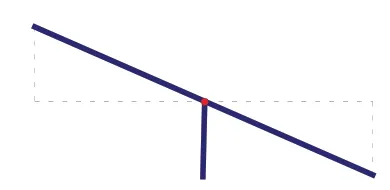
图2

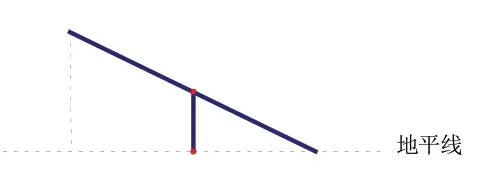
图3

2.主体实践，寻求新知

设计以下几个操作——剪纸活动，以一个贴近学生生活的问题引入，激发学生的学习兴趣，使学生领悟其本质。

（1）能否在一个三角形上剪一刀，使得分成的两块拼成一个平行四边形？（如图4）

图4

（2）若图中我们剪下的位置称为三角形的中位线（如图5），你能给出三角形中位线的概念吗？（板书课题：三角形的中位线）

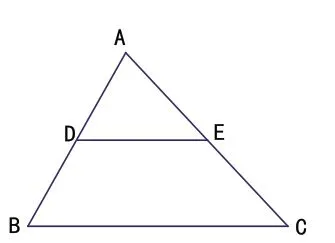
图5

定义：连接三角形两边中点的线段叫作三角形的中位线。

（3）（提问）三角形的中位线与三角形的中线一样吗？

（4）通过活动和观察，你能发现中位线和三角形的第三边有什么样的位置和数量关系？用量角器和刻度尺验证你的猜想。

（5）用所学知识对自己的猜想作出合情推理。

如图6，沿DE 将△ABC 剪成两部分，并将△ADE 绕点E 按顺时针方向旋转180°到△CEF 的位置，得到四边形BCFD。由题意，知点A、E、C 在同一直线上，点D、E、F 在一条直线上，且点A 与点C 重合。

由中心对称的性质，知FC=AD，∠CFE=∠ADE。

又由∠CFE=∠ADE，得AB ∥FC；由DB=AD，得DB=FC。

所以四边形BCFD 是平行四边形。

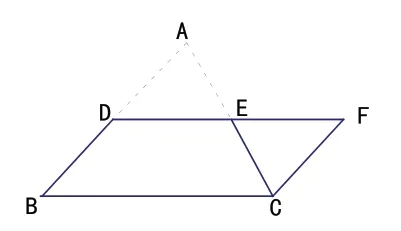
图6

归纳结论：三角形的中位线平行于第三边，并且等于它的一半。

3.知识运用，巩固新知

例1：和同学们一起解决情境创设中的问题

例2：已知三角形的各边分别为6cm,8cm,10cm，则连接各边中点所成三角形的周长多少？

例3：如图7，在四边形ABCD 中，E、F、G、H 分别是AB、BC、CD、DA 的中点。四边形EFGH 是平行四边形吗？为什么？

图7

4.归纳小结，提高认识

师生以谈话交流的形式，共同总结本节课的学习收获。

通过本节课的学习，你们在知识和方法上都有哪些收获和体会？

5.布置作业，拓展延伸

必做题：课本P104 习题3.6 的第1，3 题。

拓展延伸：（1）在四边形ABCD 中，另加条件AC=BD，四边形EFGH 是菱形，为什么？（2）在四边形ABCD 中，另加条件AC ⊥BD，四边形EFGH 是什么特殊四边形？为什么？（3）若四边形EFGH 是正方形，AC 与BD 应满足什么条件？

五、板书设计

三角形中位线定理

1.定义 例1 例2 例3

2.定理