探究文本解读在初中生数学素养培养中的路径

江苏省盐城市大丰区实验初级中学 王晓春

在一线教学中，很多教师会发现，针对学困生，无论怎样循循诱导或重点指导，都难以提高他们的学习能力；而在学科核心素养的培养过程中，部分教师也会发现，无论怎样努力，这项工作始终难以突破，学生会固定地停留在一个学习层次上止步不前。针对这种状况，很多教师将问题的症结归根于初中生的认知水平，而严格来说，虽然导致学困生出现的原因是综合性的，学科素养培养也是一个极其复杂的过程，但有些细微的环节最容易被教师忽略，其中就包括文本解读。数学是一门抽象性学科，即便学习数学的关键在于掌握它的思想方法，用数学概念、定义去解决实际问题，但前提是学生能否正确解读它们的含义。因此，文本是构成数学语言的基础，而有效解读文本则是提高学习效率、形成学科素养的前提保障。基于此，本文以初中数学教学为例，探讨了如何以文本解读来培养学生的数学素养。

一、概念文本解读，培养学生的数学素养

初中数学教材中涉及众多的概念、定义或性质，这些内容是串联数学知识的基础框架，同时也是反映知识特性的核心内容。因此，概念、定义或性质是数学最重要的指导思想，无论学习数学还是用数学解决实际问题，都需要遵照它们的基本原理，运用它们的主要方法。然而，在实践中，很多教师只注重数学概念的渗透，而忽略了学生对它们的文本解读，导致学生对数学概念的掌握似是而非，模棱两可。为此，教师可转化思路，改变方法，引导学生加大对数学概念的文本解读，使学生能够充分运用数学概念或定义，提高数学能力。

如“不等式的性质”一课，在引导学生归纳相关定义之后，笔者用练习题检验学生对定义的掌握情况。

如题：解不等式 —2x+1 ＜x+4。

生解：移项、合并同类项得-3x ＜3，系数化1 得x ＜-1。

显然，这名学生的解答是错误的，为此，笔者通过设问梳理了出现错误的主要原因。

提问：不等式成立的关键条件是什么？

学生思考并回答：用＞、＜、≥、≤、≠符号连接的式子是不等式。

问题引导：非常好，那么我们刚才学过，不等式的主要基本性质包括哪些？

学生回顾之前所学并回答：

①对称性不等式：如果x＞y，那么y＜x；如果y＜x，那么x＞y。

②传递性不等式：如果x＞y，y＞z；那么x＞z。

③不等号方向不变：如果x＞y，而z 为任意实数或整式，那么x+z＞y+z。

之后通过问题导引：假设x ＞y，z ＜0，那么xz ＜yz, 即不等式两边同时乘以（或除以）同一个小于0 的整式，在这种情况下，应当如何解读不等式的性质？出现错误的关键点在哪？

学生重新对不等式的性质进行文本解读，并解答：曲解了不等式的性质，出现错误的关键点在于解题的第二步，即“系数化1 得x＜-1”。出现错误的主要原因，是在不等式两边同除负数时没有改变不等号的方向。

如此，通过引导学生加大对不等式性质的文本解读力度，让学生对数学概念、定义或性质产生了新的认识，即：不能仅从概念本身的角度去理解其含义，更需要通过概念的字里行间来发掘它们文本构成的深意，确立数学概念的严谨性，从而改变学生粗糙的学习意识，树立起理性的学习精神，提高他们的数学能力。

二、习题文本解读，培养学生的数学能力

数学是一门抽象性很强的课程，它将生活中的具象问题抽象成为数和形，用数学的语言表现出来；同时，也将生活中解决问题的方法抽象为数量关系，概括为类比、建模、化归等等，以解题的形式呈现出来。因此，学习数学的过程实际上是学习用数学的方法来解决生活实际问题的过程。在这一过程中，学习的重点可概括为两个方面：其一是学习用数学解决实际问题的相关理论，包括上节讨论的概念、定义、性质等等；其二是学习用数学理论解决实际问题的具体方法，即解题。由此可见，解题在学习数学过程中占据着重要地位。

具体来说，习题解题是初中生最常见的错误，而出现错误的根源在于他们没能认真审题。

如图，已知△ABC 为等腰三角形，其中AB=AC，点P 在BC 上，PD ⊥AB 于D，PE ⊥AC 于E，CF 为高，求PD、PE、CF 之间的关系。

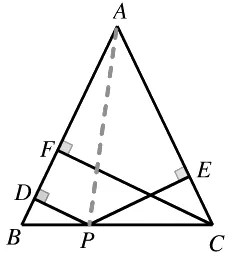
针对这道题，很多学生会出现解题错误，主要原因是学生会忽略在平面几何中，特殊图形往往是由一般图形变化而来，进而在审题时会忽略已知条件，如PD ⊥AB 于D。为此，笔者引导学生仔细审题，首先梳理题中给出的已知条件，其次明确已知和未知之间的关联，最后再运用已学知识进行解题。

即：连接AP，通过分析图形得出PD、PE、CF 均为三角形的高这一结论，最后通过计算确立三者之间的关系。

解：连接AP，∵S△APB+S△APC=S△ABC，

又PD、PE、CF 是对应三角形的高，

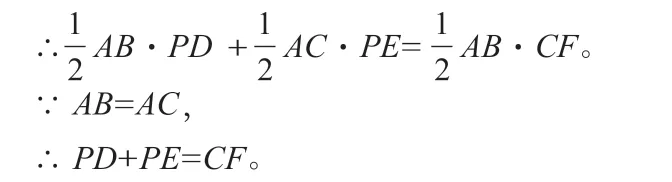
如此，通过习题文本解读，提高了学生的审题意识，改变了他们草草读题的思想观念，培养了他们的问题解决能力。

总之，数学学习是一个循环渐进的过程，而文本解读则是学习数学的基础。因此，让学生把握数学语言的独特性，感知数学文本的重要性，在此基础上，培养学生“以文立意”“以意解题”的思想观念，引导学生从最基本的文本解读入手，完善数学学习的每一个环节，对培养他们的学科素养具有重要意义。