方法联想课，让思想方法可见

虞盼云

一、“方法联想课”的课型特征

巴甫洛夫认为：“一切教学都是各种联想的形式。”联想是由一事物想到另一相关事物的心理过程，是以已掌握的知识、方法为基础，有依据、有目的、有意识的思维活动，它是一种由此及彼的思维方式。

在平时的数学学习中，学生积累和习得的各种思想、方法及策略都单一地存在于头脑中。方法联想，把反映同种思想、方法或策略的知识进行连接，将前后的问题进行联系、整合、分析，激发学生思维的活跃性，引导学生用相似的思想、方法、策略去分析问题，思考问题，巧妙地利用联想突破思维的局限性，增强思维的灵活性，从而达到解决问题的目的。

这就要求数学教师要认真钻研教材，对教材内容进行整合，将本学期甚至是小学阶段所有的内容拆分并重新整理，形成结构化的学习内容，这样才能使教学更加灵活，学生的思维更加清晰。

二、“方法联想课”的案例

在以往的教学设计中，学生在一开始学这一节课时，并不知道这节课的内容与上节课有什么不同和联系，学习的重点是什么，需要学到什么程度等。这样只能让学生如盲人摸象一般，无法构建完整的知识体系。方法联想课则采用全景式教学模式，先进行整体构架和初步感知，再进行局部的学习。

问题教学下的方法联想课的模式是：问题引发→问题探究→互动建模→解决问题。它通过问题探究提出的“问题链”引导学生更深入地进行思考，引领着学生进行分析、思辨、归纳，有效地培养学生的高阶思维能力。

我们一般从两个角度去进行方法联想课的设计，一是通过思想方法将前后知识进行联系，形成知识体系;二是通过前后知识的联系，深化学生对于思想方法的理解与感悟。接下来用以下两个案例来进行说明。

案例1：《面积与转化》

（出示一个底5分米、高3分米的平形四边形）

师：请你算一算这个平形四边形面积，说一说平形四边形面积公式是什么？

生：5×3=15（dm?）平行四边形的面积=底×高。

师：想一想平行四邊形面积公式如何推导来的？

生：我们把平行四边形转化成长方形，发现长方形的长等于平行四边形的底，长方形的宽等于平行四边形的高，长方形的面积等于平行四边形的面积，长方形面积是长乘宽，所以平行四边形的面积就等于底乘以高。

师：求平面图形的面积常常用到转化的方法，那转化方法还有哪些运用呢？今天这节课，我们一起来梳理转化方法的运用。

《面积与转化》由平形四边形引发关于转化的联想，开放的是问题，解放的是思维。顺势引发本节课的学习目标转化方法的其他运用，让学生明确这节课学习的目标，知道“去哪里”。

出示学生探究学习单：

1.哪个平面图形的面积公式是用转化推导来的？（画图说明）

2.平面图形面积之外，哪里还用到转化方法？（举例说明）

3.生活中，哪里可用到转化方法？（举例说明）

问题引发从具体的算一算、说一说、想一想开启关于转化向思想方法联想之门。问题探究则设计有层次的问题激发学生关于转化的联想：由平面图形面积的转化到面积之外的转化再到生活中的转化。学生在研究这三个问题时，逐步加深对于转化这一方法的认识与理解。

师：你能解决下面的2个问题吗？

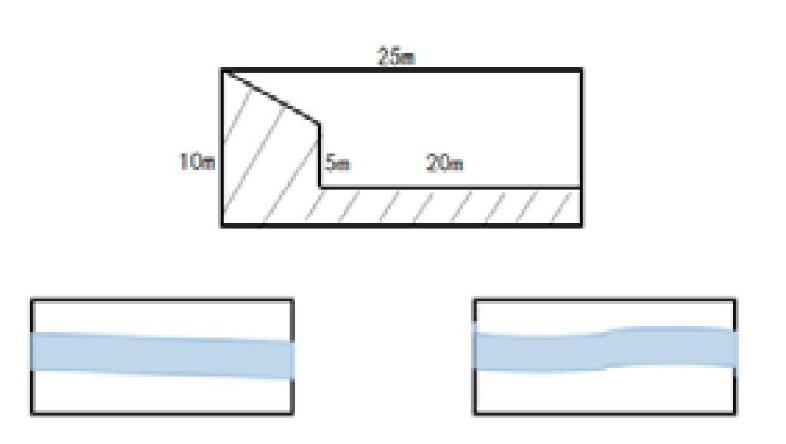
1.计算下面花圃的面积

2.有一块长20米、宽10米的长方形草地，草地中间有一条宽1米的小路，你能求出小路的面积吗？

“方法联想课”的落脚点是在解决问题环节回归数学常态教学，运用思想方法解决实际问题，不仅仅沉醉于天马行空的联想。解决问题第一题是面积公式的变式运用，巩固学生的基础知识，第二题则是转化思想的运用，进一步增强学生思维的灵活性。

案例2：《不完全归纳法》一课，教师这样设计：

（出示：a+b=b+a）

师：还记得加法交换律我们是怎么研究出来的吗？

生1：我们举例进行计算，发现交换加数以后相加结果相同。

生2：我有补充，而且我们举了好几组算式，因为一组算式有可能是特殊的。

师：3+2=2+3，4+5=5+4，1+6=6+1。这三组算式能不能说明加法交换律？

生3：我觉得不能，这三组都是一位数的，我们应该举几个位数不同的加法算式。

生4：我们还可以举几组小数的，比如0.3+0.4=0.4+0.3。这样例子比较丰富，更能够说明加法交换律。

生5：我们还可以再举几组分数的，说明加法交换律不管是小数、分数还是整数都适用。

师：像我们研究加法交换律的时候，通过举多个不同类型的例子来进行说明的方法，就叫作不完全归纳法。那不完全归纳法还有哪些运用呢？这节课，我们就一起来进一步了解不完全归纳法。

出示学生探究学习单：

1.想一想，我们之前的学习中，哪些也用到了不完全归纳法？

2.这些知识根据不完全归纳法，分别举了哪些例子进行研究？这些例子可以得到结论吗？

3.除了加法交换律，你还想使用不完全归纳法研究哪些问题？你会举出什么样的例子呢？

问题探究由第1个问题简单回忆以往使用过不完全归纳法的知识。第2个问题则具体说明不完全归纳法是如何使用的，举什么样的例子比较合适。让学生进一步理解不完全归纳法要举不同类型例子的这一特点。第3个问题则是对于不完全归纳法的运用，不设范围，不局限于数学，进一步发展学生思维的灵活性。

（作者单位：广东省东莞松山湖中心小学）

责任编辑：孙昕

heartedu_sx@163.com