数形结合视角下对运算律教学的思考

王娟

[摘 要]运算律贯穿于整个小学数学，也将运用于今后的数学学习中。数形结合思想作为一种重要的数学思想，可以有效地帮助学生理解数学知识，促进学生逻辑思维能力的发展。在运算律教学中，教师可通过以形相助、以形相辅、以形助思，促进学生把握运算本质，帮助学生变通思维，提升思维深度。

[关键词]运算律;数形结合;思考

[中图分类号] G623.5[文献标识码] A[文章编号] 1007-9068（2019）29-0025-02

在小学阶段，运算律贯穿于整个数学学习。比如，在看图列式或解决问题中加法交换律和乘法交换律就得到了广泛应用;进位加法中利用凑十法进行计算也需要加法结合律的支撑，除表内乘法及整十整百数以外的乘法计算也都离不开乘法分配律的帮助。小学阶段的运算律学习大致可分为三个阶段。第一阶段，学生结合具体的生活实例初步感受运算律，同时在解决问题和计算中不自觉地对运算律加以应用。第二阶段，也就是四年级，将会系统地学习五个基本的运算律，探索并了解运算律。第三阶段，将运算律及其运算法则迁移到小数和分数中进行应用。在北师大版四年级教材中，五个运算律的编排结构基本一致，即“观察算式—仿写算式—解释规律—表述规律—应用规律”。但学生在做题时对乘法结合律和乘法分配律的应用经常出错，说明学生对运算律的掌握仅仅停留在模仿阶段，所以教师需要为学生提供合适的学习素材，比如图形、实物、有趣的活动情境、适当的学习方法等，让学生有所观、有所感、有所悟、有所思，亲身经历知识的形成和发展过程，形成良好的数学思维习惯。

《义务教育数学课程标准（2011年版）》指出：“数学中有一些重要内容、方法、思想是需要学生经历较长的认识过程，逐步理解和掌握的，如分数、函数、概率、数形结合、逻辑推理、模型思想等。”这就明确了数形结合思想对于数学学习的重要作用。小学阶段是数形结合思想形成的启蒙和发展阶段，因此，笔者思考：能不能利用数形结合的方法帮助学生理解运算律的本质，进而合理有效地运用运算律呢？

一、以形相助，把握运算本质

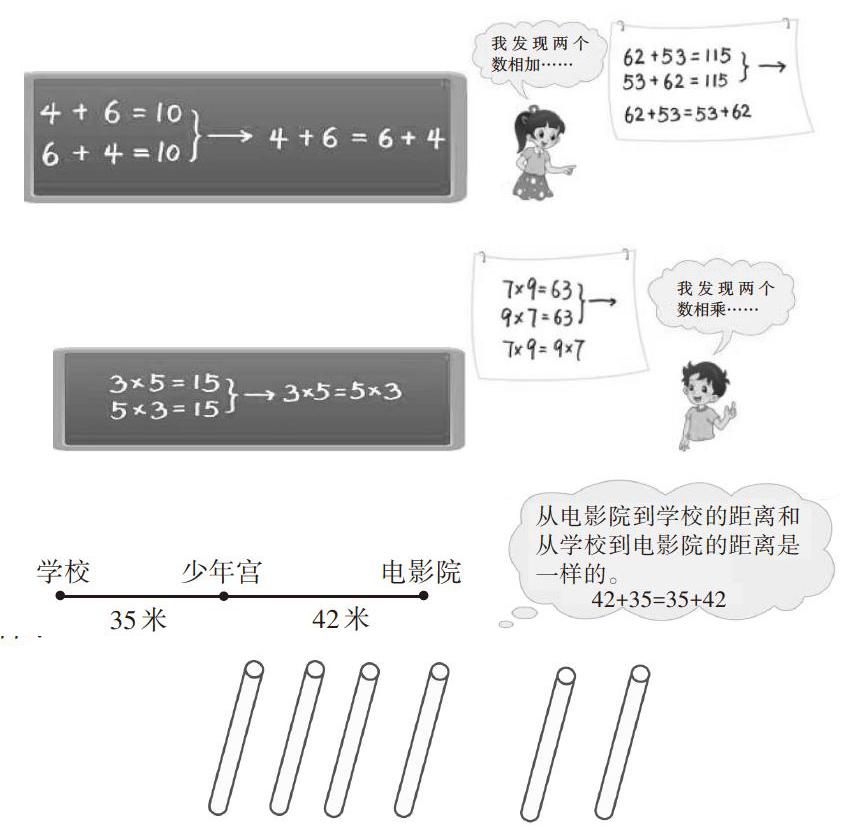
以加法交换律和乘法交换律为例，教材把它们放在一起呈现，例如出示几组算式：

先让学生观察算式，仿写算式，发现问题，然后举出事例，说明解释，确认发现。然而，能写出100个这样的算式，是不是就可以得出结论？笔者认为还是要结合加法的运算本质来说。著名数学家华罗庚曾说：“数源于数。”加法实际是数数的高级形式。在一年级的学习中，学生经常会遇到这样的题目：如下图，一共有多少根小棒？

加法的本质就是把多个数量合起来，因此有学生从左边开始数起，列式为4+2=6，有学生从右边开始数起，列式为2+4=6。不管从哪边开始数，都是把这两堆小棒合在一起，小棒的总数不变。如果小棒的堆数比较多，还可以进行结合，这就出现了加法的结合律。教材要求学生发现问题、得出猜想后再列举生活中的事例验证猜想，这是本末倒置的。仿写的算式都符合规律，就代表所有的式子都符合规律了吗？笔者认为，教材可以调整编排顺序，把一年级的看图写算式放在前面，让生活事例紧跟其后。算式只是表面现象，是表现形式，其本质上还是如何数数。教材在加法结合律的编写中也是同样的问题，在这里就不多加赘述。

总之，以“形”助“数”，可促进学生有效把握数的本质，加深数与形之间的联系与沟通。

二、以形相辅，帮助思维变通

如果说加法是相同对象的运算，那么乘法就是不同对象之间的运算。虽然现在淡化了乘法意义的教学，比如3个6写成两个乘法算式：3×6，6×3;6个3也可以写成3×6，6×3。虽然两个式子的计算结果一样，但表示的意义却不一样。因此，笔者认为仅仅观察算式，仿写算式就得出结论是不恰当的，还是要借助图形或者实物来理解。教材出示了数椅子的情景图：

在这里，乘法又回到了“数”，不管横着看还是竖着看，椅子的总数不变，只是每个人数数的习惯不一样。在解决问题时，教师可以引导学生先从数的方面去分析，进行抽象思维，再从形的方面去研究，进行形象思维。用“数”来表示“形”，以把握“形之属性”，实现数形结合，可有效发展学生的逻辑思维。

三、以形助思，提升思维深度

乘法分配律历来是教学中的重点和难点。前面学习的运算律仅仅是同一种运算，而乘法分配律就涉及了加法和乘法两种运算。

乘法分配律的字母表达式（a+b）×c=a×c+b×c很抽象，也很难理解，需要借助图形和大量的生活例子帮助学生理解，促进学生自然构建知识体系，只有这样才能避免学生只会机械模仿，面对变式无从下手。教材创设了“贴了多少块瓷砖？”这一情境，出示了两组算式“3×10+5×10=（3+5）×10;4×8+6×8=（4+6）×8”，提出问题：观察算式，你有什么发现？

笔者认为，这一情境可以分两步呈现给学生，而且要结合乘法的意义来说明。先呈现给学生正面的墙面：

学生可以很直观地看出瓷砖有蓝色和白色两种颜色，列算式的方法有很多种：

方法一：3×6+5×6=48，白色瓷砖每行有6块，共3行，所以3×6表示3个6;蓝色瓷砖每行有6块，共5行，所以5×6表示5個6;3个6加上5个6就是8个6。

方法二：（3+5）×6=48，表示白色瓷砖有3行，蓝色瓷砖有5行，一共有8行瓷砖。

方法三：8×6=48，瓷砖一共有8行，每行有6块，所以就有8个6。

看来这三种方法都表明瓷砖的总数可以用8个6表示。引发学生思考：能不能写出这样的等式：（3+5）×6=3×6+5×6=8×6=48？在学生有所感悟的基础上再出示侧面的墙壁。

侧面墙壁的瓷砖数量和正面墙壁的瓷砖数量的计算方法一样。

方法一：3×4+5×4=32，白色瓷砖每行有4块，共3行，所以3×4表示3个4;蓝色瓷砖每行有4块，共5行，所以5×4表示5个4;3个4加上5个4就是8个4。

方法二：（3+5）×4=32，白色瓷砖有3行，蓝色瓷砖有5行，一共有8行瓷砖。

方法三：8×4=32，瓷砖一共有8行，每行有4块，所以就有8个4。

引导学生思考：是不是也可以写出等式（3+5）×6=3×6+5×6=48呢？单靠这两组算式还不足以得出乘法分配律的公式，还需要大量生活事例的支撑才能抽象出乘法分配律的公式。但是通过这些式子，学生可以感受到，当出现相同乘数时都可以利用乘法的意义，最后归结于求出几个几的运算。然后在学生有所感的前提下再要求他们应用“学校要给28个人的合唱队买服装，请算算买服装要花多少钱？”，继续思考能否写出一组等式。

在大量素材的积累下，学生深刻理解了乘法分配律。可见，利用数形结合可以帮助学生化抽象为直观，进而建立解决问题的数学模型，为学生的再创造和应用做好准备。

数形结合有助于发展学生的逻辑思维，培养学生的发散性思维，激发学生的创造性思维。正所谓“数形结合百般好，割裂分家万事休”，“数形结合”是数学教学中培养学生数学学习能力的重要方式。

（责编 黄春香）