配电网故障定位技术的RTDS测试

彭博，钟少军，陈伟，徐闻博放

（云南电网有限责任公司昆明供电局，昆明 650011）

0 前言

近年来，大量的输配电网络的建设虽然提高了电力输送能力，但也造成了更多故障的发生。为了保证电能的质量和保护电网免受机械损伤，在进行故障排除之前，需要尽快检测和定位输电网以及配电网络上发生的故障，这体现了故障定位技术的重要性。先进的故障定技术能够通过从故障线路采样的参数来精确估计故障位置和线路终端之间的距离。在早期阶段，故障检测和故障定位主要通过对导体路线进行徒步巡视和目视检查完成。然而，当代电力网络的复杂配置需要更先进的故障定位方法来完成故障定位任务。自20 世纪以来，很多故障定位的方法被引入，而在所有这些引入的方法中，基于行波的故障定位方法已被普遍认为是处理配电网故障的最佳方法，因为该方法不依赖于故障线路的参数并且其性能不会受到复杂的配电网络配置的影响。本文通过模拟电网模型的方式来对基于行波的故障定位方法进行测试，以评估其在配电网故障定位中的性能。本文介绍了基于行波的故障定位方法的测试过程，并根据测试结果总结了其特点。为了进行测试，使用先进的实时模拟器RTDS 来构建和模拟单线网络模型和配电网络模型。

1 基于行波的故障定位原理

基于行波的故障定位方法的原理是基于行波在导体上的传播现象。在稳态条件下，电力系统中导线的阻抗被默认为是沿着导线均匀分布的。故障的发生将立即改变故障位置的阻抗。阻抗的变化会对电压和电流的大小产生影响，并产生一组高频行波（包括电压和电流信号）。这些行波将传播到导体的两端并且传播过程将被记录在晶格图中。一旦记录到连续波峰的到达导体两端的时间并且估算出行波的传播速度，则可以计算出现故障点与导体两端之间的距离。上述所描述的过程如下图所示。

图1 基于行波定位的方法原理

当使用基于行波的方法来定位故障时，较多使用故障电流行波，因为大多数情况下故障电流信号的幅值大于故障电压信号的幅值，并且电流信号通常较少失真。自20 世纪30 年代以来，已经引入了大量基于行波的故障定位方法。基于所需参数的不同，这种方法主要分为两种类型：基于单端行波的故障定位方法和基于双端行波的故障定位方法。

1.1 基于单端行波的故障定位方法

图2 基于单端行波方法的晶格图

从上图可以看出，由故障点F引起的行波向着导体两端传播。而基于单端行波的故障定位方法只需要记录传播到导体其中一端的行波信号。在上图情况下，导体L端装设了故障定位器，行波e'f1以及它的反射波到达导体L端的时间将被记录为tL1和tL2。一旦行波的传播熟读被估算出来（V），故障点到导体L端的距离m就能通过下面的公式计算出来：

1.2 基于双端行波的故障定位方法

基于双端行波的故障定位方法的原理将借助下图进行解释。

图3 基于双端行波方法的晶格图

从上图可以看出，但故障发生于F点时，两端行波er1和ef1分别沿着相反的方向向着导体的两端传播。假设行波在导体中的传播速度为v，导体的总长度为L，一旦记录到两段行波到达导体两端的时间T1和T2，故障点F到导体A端的距离x就能通过下面的公式计算出来：

上述两种方法，每种方法都有其优点和缺点。由于每个导体只需要一个故障定位器并且不需要同步测量系统，所以实现基于单端行波的故障定位方法更简单和更经济。但基于单端行波的方法容易受到反射行波的干扰。以图2的情况为例，导体B端反射的行波会给故障位置带来干扰。当导体B端非常靠近导体L端时，用蓝色表示的反射行波将更早到达导体L端，造成安装在母线L处的故障定位器难以识别正确的反射行波，进而导致故障位置出错。而另一方面，尽管基于双端行波的方法在每条线路上需要两个故障定位器来定位故障，使得实施该方法的投资和复杂性大大增加，但该方法的性能更加可靠和准确。

根据每种方法的优缺点，哪一种方法更合适合应该根据具体情况来决定。通常，基于行波的故障定位方法的误差在300 米以内。

1.3 故障线路选择方法

配电网网络的复杂结构和多条出线的结构给故障定位方法的实现带来一定的干扰，因为在实施故障定位方法之前需要先挑选出正确的故障线路，否则估算出的故障位置难以与正确的故障线路相匹配。因此，在进行故障定位之前，有必要缩小故障区域，这就意味着首先需要识别故障线路。本文采用单端小波系数极性法识别故障线路。以下配电网络模型被用于辅助解释故障线路的选择方法。

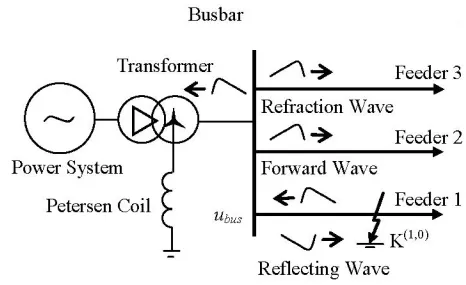
图4 辐射式配电网结构

从上图可以看出，发生在支线1 上的故障所引发的行波会向着母线传播，当故障行波抵达母线时，部分故障行波会进入支线2、支线3以及其余的电力系统中。假设i1代表支线1 上的故障电流，i2，i3和is分别代表支线2、支线3 以及其余电力系统中的故障电流，那么根据基尔霍夫定律，这些故障电流之间应该满足下列公式所表达的关系。

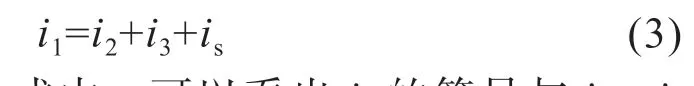
从这个公式中，可以看出i1的符号与i2、i3的符号相反，这就意味着支线1 上的行波与其余两条支线上的行波有着相反的极性。而从下图所记录的三条支线上行波的小波系数可以看出，支线1 上电流的第一个波峰为正值，而其余两条支线上电流的第一个波峰为负值。因此，我们可以断定，支线1 为故障线路。

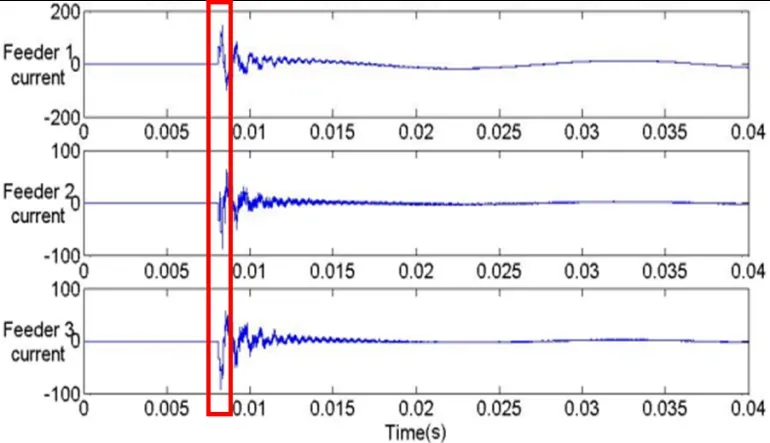
图5 三条支线的小波系数

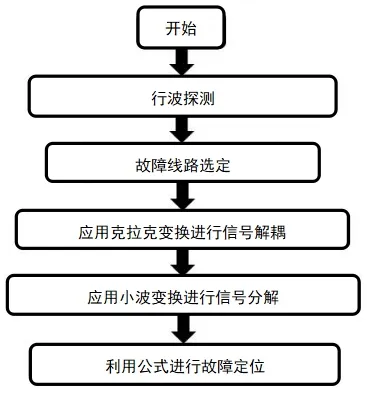
图6 行波定位方法的实施流程

1.4 行波定位方法的实施流程

行波定位方法的实施流程如图6 所示。确定故障线路后，首先应用克拉克变换法将三相信号解耦为三个独立模式，以消除三相导体中电磁耦合的干扰。然后通过小波变换法对瞬态信号进行分解，得到小波系数的波形。最后，从小波系数波形中读取波峰到达导体两端的时间，用于故障定位的公式中，以估计故障点与导体端点之间的距离。

2 RTDS动态模拟

测试中使用的仿真工具是RTDS，它是一种先进的实时数字模拟器。它从电磁暂态的角度进行电力系统仿真。实时仿真特性使得电力系统的算法得以快速和持续进行，并实现了电力系统模型与保护设备之间的直接连接，如下图所示。

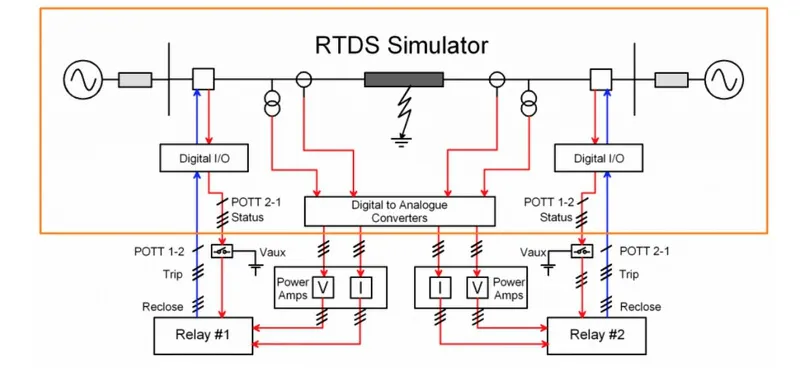
图7 电网模型与继电器的连接图

行波定位方法的测试将在两个电网模型上进行。首先，将在单线网络模型上测试基于单端和双端行波的方法，以比较每种方法的特性。然后，基于双端行波的方法将在配电网模型上进行测试，以进一步评估其在配电网络上的性能。下图显示的是在RSCAD 软件中构建的单线网络模型。

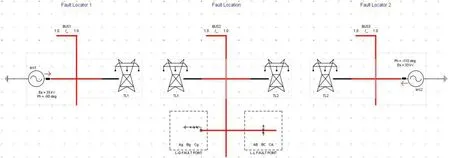
图8 RSCAD软件中构建的单线网络模型

两个故障定位器安装在靠近电压源的位置，用于记录前进和后退的行波。架空线由T-Line模型表示，能够调整故障位置。故障模型可以模拟所有类型的故障。采样频率设置为100 KHz，以保证测试的准确性。

而配电网模型以辐射式三支线的形式构建。每条支线的总长度设置为100 km，三条支线的电压水平分别设置为35 kV，10 kV 和0.4 kV。在每条支线的两端都安装了两个故障定位器，用于实施基于双端行波的方法。以RLC 形式模拟每条支线的负载，并使用相同的T-Line 模型来模拟架空线。完整的配电网络模型如下图所示。

图9 RSCAD软件中构建的配电网模型

3 开展测试

图10 行波传播速度的估算方法图

在进行基于行波的故障定位方法的测试之前，首先需要估计行波的传播速度，因为它是计算故障定位算法中的必要参数。传播速度将通过单端行波定位的方法理论进行估计。估算过程借助下图进行解释。首先，一个故障被故意设置于距离导体A端m 的位置。然后，暗转与导体A 端的故障定位器将会捕捉到行波ef1和其反射波的到达时间。最后, 行波的传播速度能够通过变换的单端行波定位方法的公式计算得出，该公式如下：

以距左端10 km 处出现的相间故障为例，平方小波系数图记录如下。

图11 故障电流的平方小波系数图

两次到达时间分别为0.04004 s和0.04012 s，传播速度计算公式为：

所有估算结果的平均值为286758.5217 km /s。该值将被用作所有故障定位算法计算中行波的传播速度。

3.1 单线网络模型故障定位测试

首先，将在单线网络模型上测试两种基于行波的故障定位方法。测试设置的故障位置到左端的距离从10 公里变化至90 公里，测试涵盖所有类型的故障情况。一旦由故障引起的行波被终端故障定位器记录下来，克拉克变换和离散小波变换将被应用于故障信号以获得小波系数的波形。从小波系数的波形中，可以读取波峰的到达时间，然后用它来计算故障位置和线路起始端点之间的距离。

通过估计距离和实际距离之间的比较，百分比误差将在以下等式中计算以评估精度。

其中D实际和D分别代表实际距离和估算距离，L代表导线的总长度。

基于单端行波定位方法的全部测试结果发现，在处理同一故障位置发生的不同类型的故障时，基于单端行波的方法具有相同的百分比误差，这意味着故障类型不会影响这种方法的性能。而根据不同故障位置的准确度变化来看，当故障位置离测量点最远时出现最大误差。因此，可以得出这样的结论，当故障位置远离测量点时，基于单端行波的故障定位方法的精度将大大降低，而故障类型不影响该方法的精度。基于双端行波定位方法的测试结果汇总表明，基于双端行波的故障定位方法的性能也不会受到故障类型的影响。然而，这种方法的最大误差出现在探测距离故障定位器最近的故障时，当故障位置接近导线中点时，精度大大提高，发生在导线中点的故障定位误差百分比甚至为0。

通过比较这两种基于行波的故障定位方法的测试结果，很明显可以看出，基于双端行波的方法具有较高的整体精度。此外，基于双端行波的方法不受噪声和其他反射波的干扰，因为用于故障定位方法中的前向和后向行波的第一波峰通常具有最大振幅，使得它们容易被抓获。接下来，基于双端行波的故障定位方法将在配电网络模型上进行测试，以便进一步评估其性能。

3.2 配电网模型故障定位测试

在配电网模型上进行的测试与单线网络模型故障定位测试具有相似的程序。唯一不同的是在处理故障信号之前将应用故障线路选择方法。在识别出故障线路后，将对所记录的行波实施克拉克变换和离散小波变换，以获取小波系数的波形。根据从小波系数波形中读取的波峰到达时间，可以通过公式计算来估计故障位置。配电网故障定位测试中的变量只是故障位置与每条支线起始端点之间的距离，因为在之前的单线网络模型的故障定位测试中已经确定故障类型对基于行波的故障定位方法的精度没有影响。测试程序将在配电网络模型的所有三条支线上重复。单端小波系数极性法能够以100%的准确度识别故障线路，并且基于双端行波的故障定位方法在配电网模型上也具有很高的精度。

4 结束语

本文介绍了基于行波的故障定位方法的RTDS 测试。首先在单线网络模型上测试了基于单端和双端行波的故障定位方法，以分析每种方法的特性。然后基于双端行波的故障定位方法在配电网模型上做了进一步测试。所有的模型都是在RSCAD 软件（RTDS 的相关专有软件）中建模和模拟的。

在所有测试之后，可以得出如下结论：

l）单线网络模型故障定位测试结果证实基于单端行波的故障定位方法能够很好地定位发生在故障定位器附近的故障。但是，当应对导线中点附近出现的故障时，基于双端行波的故障定位方法具有更好的表现。

2）配电网模型故障定位测试结果表明，单端小波系数极性法是一种精确、合适的故障线路选取方法，可用于故障定位技术实施前缩小故障区域，而基于双端行波的故障定位方法在配电网故障定位方面具有优异的性能。