交变电场场源定向技术
李鹏,张文斌
(昆明理工大学机电工程学院,昆明 650504)
0 前言
在静电起电及放电过程中,利用电场信息、电磁辐射信息、声音信息等进行目标探测及定位是当前国内外研究的热点[1-3]。基于电场信息的目标定位方法在军事、电力领域都有广泛应用。在军事方面,目前的隐形战机、导弹等都具备较强的隐身能力,但是由于在空中飞行的过程中和空气摩擦,会产生静电信息[4-5],可利用探测器中各阵元之间的位置关系以及阵元所测量到的电场信息(电场强度)与目标方位之间关系获得目标的方位信息。在电力方面,可用于输电线路的故障定位、电力电缆绝缘损伤的故障定位等[6-7],高压输电线发生故障时会产生暂态信号,该信号包含了大量的故障及位置信息,通过特征提取及数据分析等方法可找出故障发生的位置。综上所述,基于电场信息的定位方法的研究对多个行业都具有重要的意义。
一种可靠的静电定位方法可准确的得到探测器与带电目标之间的距离和角度信息,基于此方法可实时计算出穿戴探测器的人、无人机、机器人与带电设备之间的方向和距离从而可准确达到安全距离预警的目的。而安全距离预警技术的研究已比较成熟,也取得了很多成果。传统的电力预警装置需要判断出带电设备、输电线的电压等级,然后设定相应安全距离处的电场报警阈值,通过阈值报警的方式实现安全距离预警[8-10]。但是,它们都无法获得危险场源的方向信息,无法准确判断作业人员的安全状态,且电压等级的识别技术也较复杂。
为了实现探测器的可穿戴,探测器的体积应该设计的足够小;为了提高测量精度,应该考虑阵元间的耦合干扰及阵元的个数;为了能得到简单可行的定位算法,应该选用合适的阵元布局。目前,常用的定位系统有:线阵、面阵。其中,线阵能够得到目标的仰角和距离,且具有算法简单易于实现的特点,但线阵不能计算出方位角;平面阵列不仅可以确定出探测器中各个阵元与目标之间的距离还可得出仰角和方位角[11],但平面阵列的算法较为复杂。本文结合了线阵和面阵的优点,通过各阵元间输出的大小关系进行目标的定向即可将计算复杂的面阵转换成计算容易的线阵。可在能见度低的环境下快速得到带电设备、故障输电线路的方向,减少了维修时间从而减少了停电带来的损失。
1 定位原理
平面圆周阵列如图1 所示,其中n+1 个电场传感器均匀的阵列在同一圆周上,将其顺时针进行至的编号,探测系统中心布置一个传感器。其中,探测系统半径为,以探测系统中心o 为原点建立球坐标系。设传感器g0、g1、g4布置在轴上,为探测系统的对称轴,第i 个传感器gi与oy轴的夹角为φi。此外,当探测器接近地面时,电场线垂直于地面,可认为穿过探测器的电场为均匀电场。
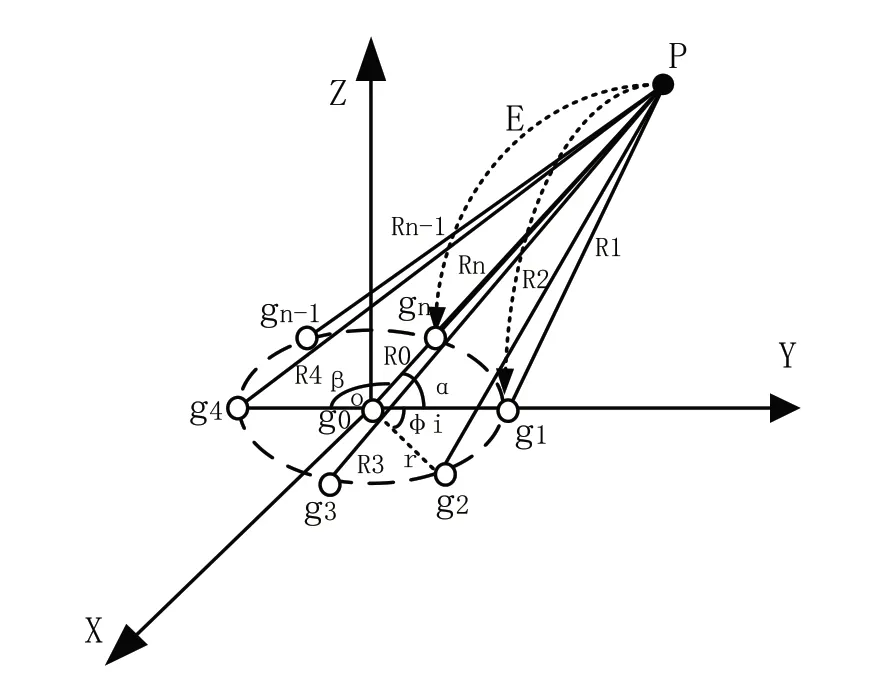
图1 探测器示意图
本文的带电目标为频率50-60HZ 的工频场源,由于工频电场属于“准静态场”,故可用静电场理论进行工频电场的理论分析[12]。平面圆周阵列虽然可计算出目标的方位,但是平面圆周阵列所确定的目标P(R,θ,ψ)是个三维坐标,求解过程较复杂。故需要进行降维处理,利用各阵元间所测场强值的大小关系可确定出探测器与目标之间的相对位置即方位角ψ,从而将平面阵列简化为比较容易计算的线阵,可计算出探测器中心与目标间的仰角、距离。
根据电场强度与目标所带电荷量间的关系可知[13]:

式中,Ei为电场传感器处被测点的场强,其中i=1,2,…,n;Q为目标所带电荷量;ε0为空气介电常数;Ri为阵元gi与目标之间的距离。
由式(1)可得出:

由式(2)可以看出,目标的电荷量Q与Ri2成正比、与Ei成反比。图1 时刻为目标位于探测系统对称轴oy上方。再根据等腰三角形定理可得此刻:R2=Rn、R3=Rn-1,故根据式(2)可得到如下唯一的映射关系:

通过式(3)即可确定出带电目标所在方向,即将三维坐标P(p,θ,ψ) 转化为比较容易计算的二维坐标P(p,θ)问题进行求解。那么,根据式(2)可以进一步得到:
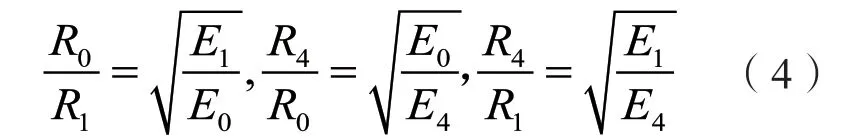
由图1 的几何关系可得到:

又根据三角形的诱导公式可得:
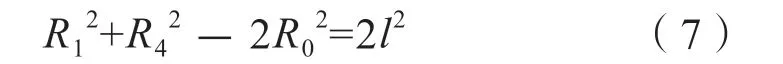
式中,l为各阵元间的距离,结合式(4)、(5)、(6)、(7)可推出目标与探测器中心的距离和仰角分别为:
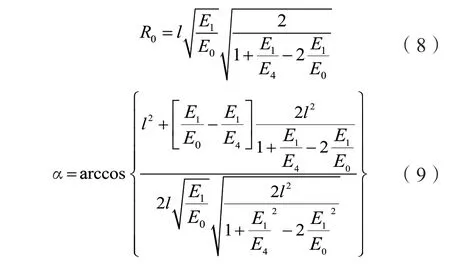
由上述分析可知,目标定位技术可分为2部分研究。第一部分为通过各阵元gi之间的关系判别出目标的方向即方位角;第二部分为根据式(8)、(9)可得出以及仰角1-α。本文对第一部分进行了深入的研究。
2 探测系统的设计
2.1 传感器布局参数
根据式(3)可知要实现目标的定向只需使用圆周上的6 个传感器即可,因此为了便于分析本文省略了探测器中间的传感器g0。
为了提高定位的精度,除了传感器自身的测量精度外,传感器的布局方式也是影响测量精度的关键问题之一。通过对传感器的半径大小τ、探测器半径r、阵元之间的距离l、阵元个数n 进行合理搭配以得到最佳的定位精度。
电场传感器的感应板本身就由金属片构成,在电场中金属表面的感应电荷会产生一个新的电场,这不仅会使自身周围的电场发生畸变还会影响附近传感器的测量精度,称之为耦合干扰。当两传感器的间距足够远时,可以忽略上述的耦合干扰,但是为了实现可穿戴探测器的体积就不宜过大。这就需要找到电场传感器的半径τ与两传感器间的间距l的关系,文献[14]通过镜像法推导得出当传感器半径τ与两电场传感器的间距l之比小于等于0.05 时,即可认为两传感器间不存在耦合干扰。故,这可以作为传感器布局的第一个条件。
本文设计的探测器将来需要安装于安全帽内实现可穿戴,这不仅不会干扰作业人员的正常工作,安全帽还能保护探测器不受外界伤害。目前,通常使用的安全帽外壳可等效为半径11cm 的圆。为了使两传感器间的距离最大,故可将传感器布置在安全帽外壳为最佳,即探测器半径r=11cm。这可以作为传感器布局的第二个条件。
在探测器半径确定的条件下,传感器的个数n 只与传感器间距l有关。从理论分析可知,圆周上传感器个数n=4 就可以实现目标的定位,但为了提高测量精度应增加传感器的个数[15]。这可以作为传感器布局的第三个条件。
根据上述的分析,可得传感器布局的约束条件为:

根据式(10)可知,在满足条件一和条件二的情况下,若要增加传感器的个数,就得减小传感器的半径τ。再根据上文提到的定位原理可知,传感器个数必须得为偶数个,故n 的取值范围为6,8,10…,若n 取6 则可得到如图2所示的探测系统示意图。

图2 n=6时探测系统示意图
如图2 所示,6 个传感器均匀阵列于同一圆周,且r=l=11 cm,此时由条件一计算可得传感器半径应小于等于22 mm。在测量过程中传感器不宜过小,过小的传感器会导致感应电荷量过小而检测不到信号,且加工难度大,难以保证传感器的一致性。故本文选择半径为2 cm 的传感器,那么为了满足式(10)探测器尺寸参数取n=6,τ=2 cm,r=11 cm。
2.2 探测器硬件设计
根据上述得到的尺寸参数,设计了探测系统结构图。其中6 个半径为20 mm、厚度为0.2 mm 的一维圆形电容式工频电场传感器以步长为60°的方式均匀阵列于同一圆周。探测器采用锂电池供电,传感器用于采集交流电场的信号,该信号通过信号线传输给主板进行数据处理,最后通过无线通信模块将数据传到显示终端。其中,每2 个传感器、主板及电池构成一个采集系统,为使主板及电池对传感器的影响一致,采用3 套同样的采集系统进行数据采集;本实验所使用的传感器输出为电场强度值,单位为V/m。
3 实验验证
3.1 实验平台搭建
为验证本文提出的目标方向判别方法,搭建了试验平台。其中,探测器置于离地面高为10cm 的绝缘桌上;交流场源采用离地面高度为1m 的交流高压实验台,可产生50 HZ 的稳定电压,可从0 kV 调节到110 kV。本文的理论中将场源假设为点电荷,那么在选择测量位置时应使测量距离为场源尺寸的3~6 倍[16-17]。
3.2 实验验证及分析
在电力行业中通常带电目标处于静态,接近目标的人处于运动状态,这可能会导致探测器与目标的方向随时发生变化。为模拟探测器与目标之间相对方向的变化,本文采用旋转实验法进行验证,即以场源位于og1 方向上方时为初始点,步长为30°将探测系统绕自身在XOY 平面旋转360°。如图3 所示,此外每旋转30°记录各个电场传感器的输出值。
按照操作规范将无局放高压台调节到30 kV,并在满足测量位置与场源距离为场源尺寸的3~6 倍的条件下任取三个点进行实验。实验结果如图4 至图6 和表1 所示,其中,E1~E6为1 到6 号传感器的输出值。

图3 旋转示意图

表1 不同角度、位置各传感器之间的关系实测
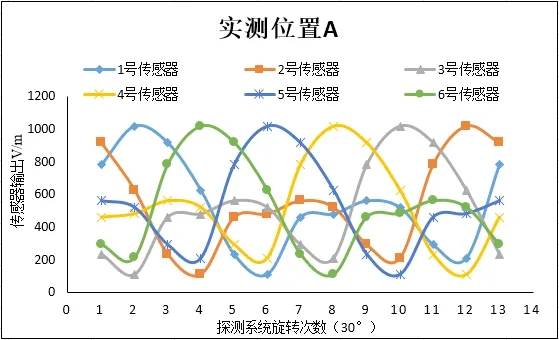
图4 位置A实测值

图5 位置B实测值
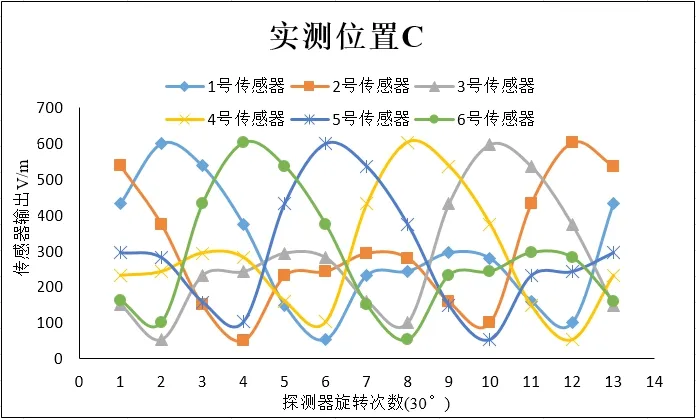
图6 位置C实测值
通过图4 至图5 可发现,在不同位置探测系统每转过相同的角度,各传感器输出排序从大到小保持一致,且当旋转到不同角度时各组排序的次序不同。由表1 还可知道,对于本文的场源只需知道每组排序中前2 个传感器的排序次序就可判断出场源的方向。例如,首先把探测系统任意放置在A 位置,然后观测传感器输出的排序,若出现表1 中的排序即可直接判断出场源的方向,若没有,则需要人为的将探测系统旋转一个角度,如果旋转后传感器输出排序中前2 个传感器排序次序为E1>E6,即可认为场源位于og2方向上方,且g2与场源距离最近,无需知道所有传感器的排序从而提高了场源定向方法的容错率。
实验结果与理论式(3)有差异,这是因为在阵列布设过程中的尺寸误差和测量过程中周围环境引入了噪声,导致当目标位于探测器对称轴线时,布置在对称轴两侧的对称传感器所测值略微不同。但是从实验结果可看出利用各阵元之间的测量值大小关系依然可用于目标方向的判定。
4 结束语
本文运用平面圆阵和线阵的优点对低频交变电场场源定位的方法进行了推导,得到利用各阵元间所测场强的关系获取场源方向的方法,在已知方向后还推导出了空中工频场源的仰角、距离的数学解析式。为提高探测器的测量精度,研究了传感器的布局方式,得到探测器半径大小为11 cm、阵列角度为60°、传感器间距为11 cm、传感器个数为6 个、传感器半径为2 cm。最后通过搭建的无局放高压试验台分别选择不同的三个位置对该方法进行了验证,实验结果表明:虽然实测结果与理论分析存在一定的差异,但依然可用该方法进行场源方向的判别。
在判断出场源的方向后,利用本文推导的距离和仰角公式可得到探测器与场源的距离和仰角,但是测量过程中引入的环境噪声以及布设传感器的尺寸误差都会引起定位误差,这也是本文接下来继续深入研究的内容。

