分数阶细胞神经网络的动力学特性分析及控制设计
王仁明 陈 昱 张赟宁 王凌云
(三峡大学 电气与新能源学院, 湖北 宜昌 443002)
分数阶系统模型能够更加真实准确地描述现实世界中存在的系统,越来越受到科学界和工程界的重视.许多系统的数学模型都可以采用分数阶微积分描述,如:热流体流动过程[1],无人机飞行控制[2],电磁波和粘弹性系统[3]等.许多分数阶系统的动态行为是混沌的或超混沌的,如:分数阶Chen系统[4]、分数阶Lu系统[5]、分数阶Lorenz混沌系统[6]、分数阶蔡氏电路[7]等.分数阶混沌系统的阶数引起的复杂性也让其比整数阶混沌系统具有更高的保密性,因此,分数阶混沌系统在数据加密[8]、保密通信[9]等领域具有广泛的应用前景.从而,分数阶系统的动力学特性分析与同步控制设计被广泛研究,如自适应滑模控制同步[10]、自适应控制[11]、状态反馈控制[12]等.
细胞神经网络(cellular neural network,CNN)由Chua 和Yang于1988年提出[13],是一种局部互联、双值输出的信号非线性模拟处理器,适用于超大规模集成电路实现.这使得CNN的研究成果广泛应用于生物医学、自动控制、模式识别、保密通讯、图像处理等领域[14-16].同时,CNN也是一种非线性系统,当满足某些特定条件时,在CNN中能够产生混沌现象[17].大多数CNN的研究成果都是基于整数阶模型得到的,如CNN在图像加密中的应用[18]、忆阻细胞神经网络在图像处理中的应用[19]等.事实上,整数阶系统是对实际系统的理想化处理,分数阶模型相比于整数阶模型,能显示出比整数阶模型更符合实际的特性,如更高的灵敏性和记忆性,可以更精确地描述系统的复杂特性及其变化.若以分数阶模型描述CNN,则更准确及更具有实际应用价值,而这种研究并不多见.因此,本文构建了一个四阶分数阶CNN系统模型,分析了其动力学特性,如混沌吸引子、时序图、Lyapunov指数、平衡点的稳定性.同时也验证了在相同的系统参数和初始条件下,系统的混沌吸引子结构依赖于分数阶阶次的取值,并给出了系统出现混沌的参数范围.设计了状态反馈控制器镇定系统,并通过仿真结果验证了设计的正确性.
1 细胞神经网络的分数阶模型
分数阶微积分是整数的积分和微分的推广.数学家提出了多种分数阶微积分的定义,本文采用Caputo定义分析和设计系统.其定义如下[20].

(1)
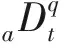
在细胞神经网络中,第i行,第j列的神经元只与周围相邻的神经元连接.CNN的状态模型可以简化为如下形式
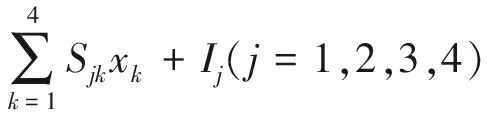
(2)
其中,xj是第j个细胞的状态变量,aj,Ajk,Sjk是常数值.若令式(2)的参数值如下:s11=s12=s21=s24=s33=s34=s42=s43=0,a1=a2=a3=0,Ajk=04×4,I1=I2=I3=I4=0.则可以得到式(3)的CNN状态方程模型:

(3)

与模型(3)对应的分数阶CNN模型为:

(4)
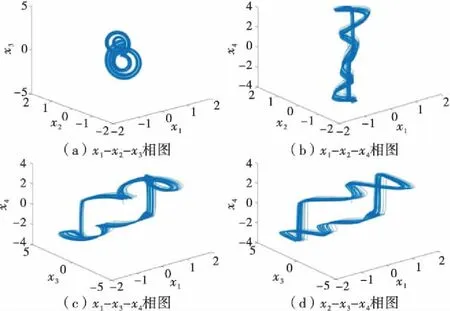
式中,q=(q1,q2,q3,q4),0 调整四阶分数阶细胞神经网络系统(4)的参数值,可以使其产生混沌及超混沌现象.若取参数为:a1=a2=a3=0,I1=I2=I3=I4=0,a4=200,Ajk=04×4,s13=s14=-1,s22=2,s23=1,s31=14,s32=-14,s41=100,s44=-100. 令q1=q2=q3=q4=0.95,取步长为0.05,初始状态为x1(0)=0.1,x2(0)=0.2,x3(0)=0.2,x4(0)=0.2.用Adams-Bashforth-Moulton预估校正方法[21]对系统(4)求解,可得系统(4)的混沌奇异吸引子和状态时序图分别如图1~2所示. 图1 四维分数阶细胞神经网络系统3-D混沌吸引子相图 图2 四维分数阶细胞神经网络系统状态分量时序图 图1显示,在特定的参数值、初始状态以及分数阶阶数的情况下,系统(4)呈现混沌状态.可以进一步验证当q1,q2,q3,q4变化时,系统(4)的混沌吸引子会随之变化甚至消失.若取q1=q2=q3=q4=0.92,而参数和初值不变时,其相图如图3所示. 图3 q1=q2=q3=q4=0.92时,四维分数阶细胞神经网络系统3-D相图 当q1=q2=q3=q4=0.87而参数和初值取值不变时,其相图如图4所示. 图4 q1=q2=q3=q4=0.87时,四维分数阶细胞神经网络系统3-D相图 当q1=q2=q3=q4=0.76而参数和初值取值不变时,其相图如图5所示. 图5 q1=q2=q3=q4=0.76时,四维分数阶细胞神经网络系统3-D相图 通过上面4组混沌吸引子相图,可以清楚地观察到,当系统的分数阶阶次发生改变时,系统的动态特性发生了改变.当0.77≤q≤1时,系统的混沌特性是存在的,而当q<0.77时,系统的混沌特性不存在. 由于在式(4)中,f(xi)=1/2(|xi+1|-|xi-1|)为非线性函数,所以,按照D1={x||x4|≤1};D2={x||x4|≥1};D3={x||x4|≤-1} 3个区域来求解系统的平衡点.令式(4)右边等于零,得到系统的平衡点为xeq1=(0,0,0,0)T,xeq2=(2,2,-4,4)T和xeq3=(-2,-2,4,-4)T.式(4)的Jacobi矩阵为: (5) 在3个平衡点处的雅可比矩阵分别为: 可以求得平衡点处的特征值见表1. 表1 平衡点的雅可比矩阵的特征值 由表1知,在(0,0,0,0)T处,4个特征根的实部均为正实数,所以,该平衡点为不稳定平衡点;在(2,2,-4,4)T和(-2,-2,4,-4)T处,特征根λ2,λ3的实部为正实数,λ1为负实数,λ4为正实数.所以,该平衡点也是不稳定平衡点.平衡点的不稳定性也导致了系统(4)的混沌现象. Lyapunov指数是表征动力学系统相邻轨道平均分散率的物理量,体现了系统动态行为的内在特征.对于混沌系统,至少有一个正的Lyapunov指数.Lyapunov指数的计算公式如下: (6) 式中,F′(x)为系统所对应的雅可比矩阵,xi为平衡点. 由式(6)知,在平衡点(0,0,0,0)T处,Lyapunov指数分别为132.615 3,2.199 2,0.980 9,1.169 1;在平衡点(2,2,-4,4)T处,4个Lyapunov指数值分别为0.818 4,0.419 4,0.197 4,-67.952 3,其中有3个为正数.此外,在参数和初始值不变的情况下,改变系统分数阶的阶数值也影响Lyapunov指数,这种影响可以通过Lyapunov指数谱直观地表示出来.表2显示qi(i=1,2,3,4)取不同值时的Lyapunov指数值,图6则为平衡点(2,2,-4,4)T的Lyapunov指数谱. 图6 不同qi(i=1,2,3,4)取值的Lyapunov指数谱 qω1ω2ω3ω40.980.72410.33840.2391-78.65070.900.99960.39910.2624-31.46740.872.74951.12290.26440.36320.76161.89521.7445-0.00900.2050 由表2可知当q=0.76时,4个Lyapunov指数中有3个正数,而由图6可知,此时系统是没有混沌现象.因此,只通过Lyapunov指数这一个指标难以判别一个系统是否能够产生混沌. 为设计分数阶CNN系统的控制律,下面的引理是有用的. 引理1[22]、设系统(4)的阶数q1=q2=q3=q4=q∈(0,1),当且仅当det(λI-Ji)=0求得的所有特征根都满足|arg(λ)|>(qπ)/2时,对应的平衡点是渐近稳定的. 阶次为q的分数阶混沌系统的稳定区域如图7所示. 图7 分数阶系统的稳定区域 由引理1和图7可以看出,对于分数阶混沌系统,若0 受控的细胞神经网络混沌系统(4)可以重写为如下形式: (7) 设计(7)的状态反馈控制律为: u(t)=K(x(t)-xeq) (8) (9) 若误差系统(9)在原点渐近稳定,则受控系统(8)在其平衡点亦渐近稳定. 根据细胞神经网络系统的特性,分以下几种情况讨论: 由det(λI-J4)=0,求得其特征根为:λ1=-98.961 0,λ2=-49.389 4,λ3=-4.398 1,λ4=-2.251 6,所有特征根都具有负实部,因此,误差系统在原点渐近稳定.从而原系统在平衡点(0,0,0,0)T处渐近稳定.取初始值e(0)=(0.1,0.2,0.2,0.2)T,仿真结果如图8所示. 图8 在xeq1=(0,0,0,0)T处的状态轨迹 由det(λI-J5)=0知其特征根为λ1=-40,λ2=-80,λ3=-1,λ4=-3,特征根均具有负实部.因此,该平衡点处,误差系统轨迹在区域D1={e|-5≤e4≤-3;e1,e2,e3∈R}与区域D2={e|e4<-5 ore4>-3;e1,e2,e3∈R}之间切换.令初始值e(0)=(-3,-2.5,-2,-4.5)T,仿真结果如图9所示.可知误差系统(9)在原点渐近稳定.从而受控系统(7)在平衡点xeq2=(2,2,-4,4)T渐近稳定. 图9 平衡点xeq2=(2,2,-4,4)T处的相图及状态轨 图10 平衡点xeq3=(-2,-2,4,-4)T处的相图及状态轨迹 本文在已有的整数阶细胞神经网络模型的基础上,构建了一个四阶分数阶细胞神经网络系统模型,通过分析系统Lyapunov指数,混沌吸引子,平衡点稳定性等,研究了系统的动力学行为.通过分析可知,在参数值、初始值不变的情形下,调整阶次的数值可以产生复杂的混沌现象.此外,基于状态反馈控制策略设计了一个控制器来镇定系统的不平衡点,并通过数值仿真验证了设计的有效性.2 分数阶细胞神经网络的动力学分析
2.1 混沌吸引子



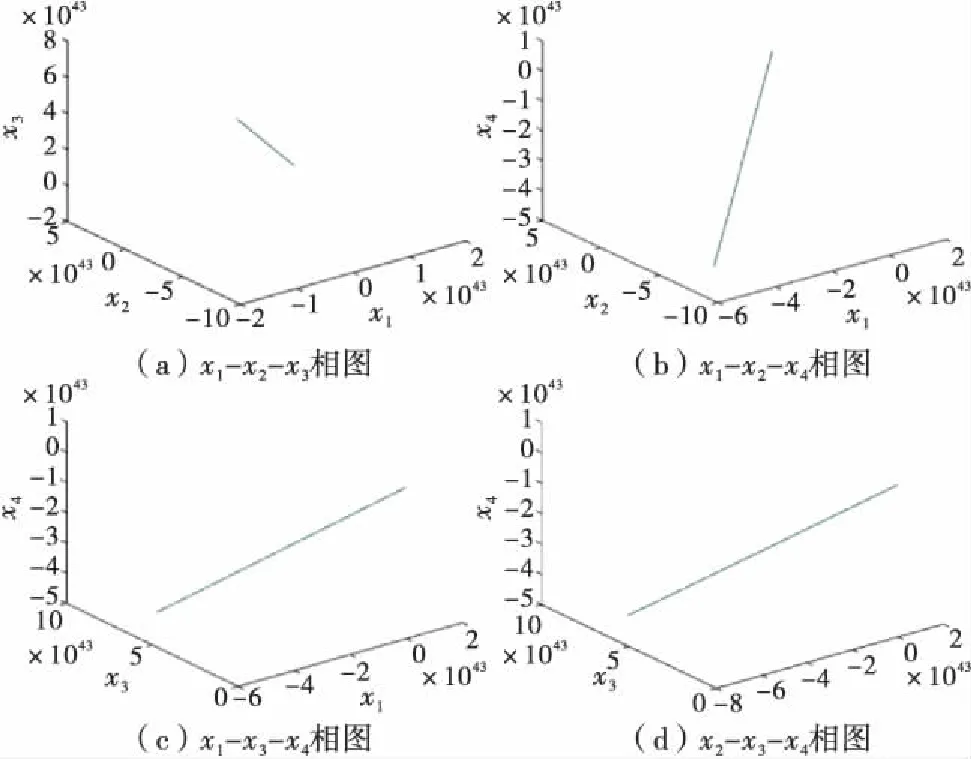
2.2 平衡点的稳定性分析
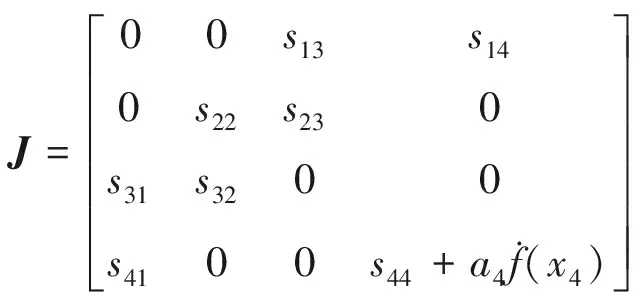

2.3 Lyapunov指数



3 分数阶细胞神经网络的控制设计





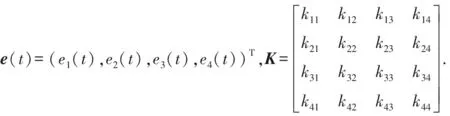




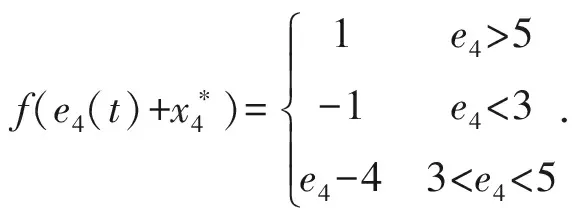

4 结 论

