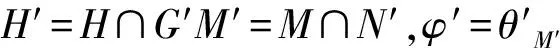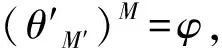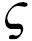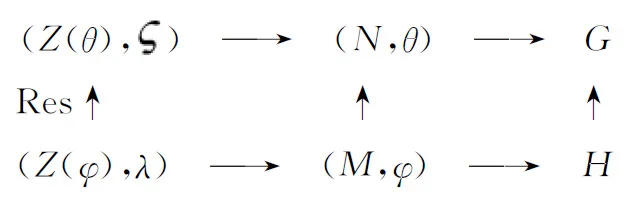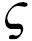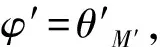特征标三元组的诱导子映射
常学武,韩丽
(山西大学 数学科学学院,山西 太原 030006)
0 引言
在有限群的表示论中,研究正规子群与群本身的特征标之间的相互影响和确定关系,即通常的Clifford理论,具有重要的意义和广泛应用。在Clifford理论中,核心概念是所谓的特征标三元组T=(G,N,θ),其中G是一个有限群,N◁G为G的正规子群,θ∈Irr(N)为N的一个不可约复特征标且为G-不变的。关于特征标三元组的研究可以参考[1-5]。
关于特征标三元组的研究,目前已经取得了丰富的内容和成果。特别是为了证明M-群的若干著名猜想以及处理特征标对应理论中相关的重要问题,Dade在系列论文[6-8]中创立了特征标三元组的稳定子极限理论,并深入考察了极限情形下的不变量。Isaacs在[9]中借助特征标三元组的诱导子和拟本原等概念,给出了Dade一个主要定理的简化证明。此外,Loukaki在其博士论文[10]中研究了一种新型的稳定子极限,即所谓的线性极限,并与Dade合作在[11]中对线性极限做了系统的探讨,特别是引入了特征标三元组之间的覆盖关系。Lewis在[12]中给出的Loukaki定理的简化证明以及Loukaki本人在[13]中证明的若干定理,均使用了特征标三元组的线性极限所提供的图表约化技术。我们在[14]中也使用特征标三元组的线性极限证明了关于M-群的几个结果。而特征标五元组的线性极限也得到了相应的研究[15]。
事实上,即使从范畴的观点看,特征标三元组亦可视为基本的研究对象,值得展开系统的研究。特别地,为了更好地发挥其特有的技术功效,需要深入地考察其各种子对象的基本联系。从文献中所使用的图表证明技术看,一个特征标三元组至少有三个极为重要的子对象,即Dade命名的诱导子,限制子和覆盖子,均需要做更多的探讨,它们在很多特征标定理的证明中发挥了重要作用。我们在此先给出相关定义。
固定一个特征标三元组T=(G,N,θ),如果R=(H,M,φ)也是一个特征标三元组(按定义即M◁H且φ∈Irr(M)是H-不变的),使得G=NH,M=N∩H,并且φ在θ下方,即φ是θM的一个不可约分量,则称R为T的一个子三元组,记为R≤T,如图1所示。
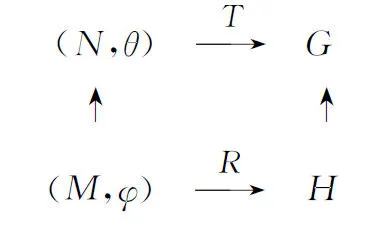
Fig.1 Character subtriple
图1 子三元组
进而,如果还有φN=θ,则称R为T的一个诱导子;如果φ=θM,则称R为T的一个限制子;如果Z(θ)H=G,则称R为T的一个覆盖子。以下将看出覆盖子其实是一种特殊的限制子,见本文引理2。
在特征标三元组的研究中,一个基础的问题是探讨任意两个拟本原的诱导子,何时具有相同的次数或同构的截面,在此所使用的主要技术是考察特征标三元组的诱导子与其限制子之间存在的特征标对应。方便起见,我们记Ind(T)为特征标三元组T的所有诱导子的集合,本文将重点研究特征标三元组的诱导子集合与其限制子的诱导子集合之间的对应关系,其理论意义和重要性在于提供一种更强的范畴观点和图表约化技术,可用来简化和改进已有的相关重要定理。
定理A设T为特征标三元组,R为T的一个限制子,则可构造一个映射,

保持诱导子的指数不变,即|T:T′|=|R:R′|.
我们称上述映射f为从三元组T到其限制子R的诱导子映射。关于f的构造定义,以及相关的术语和符号,见本文定理1。下述结果见本文定理2,描述了诱导子映射的像,推广了[16]中的主要定理。
定理B设T=(G,N,θ)为特征标三元组,R=(H,M,φ)为T的一个限制子。如果R′=(H′,M′,φ′)为R的一个诱导子,使得(M′,φ′)为N的一个诱导源,则T存在一个诱导子Τ′=(G′,N′,θ′),使得R′为其一个限制子,即f(T′)=R′.
使用覆盖子的概念,可给出诱导子映射恰为双射的条件,见本文定理3。
定理C设T为特征标三元组,如果R为T的一个覆盖子,则诱导子映射f:Ind(T)→Ind(R)为双射,并且任意诱导子T′∈Ind(T)的像R′=f(T′)∈Ind(R)也是T′的一个覆盖子。
在本文最后,还探讨了诱导子映射所保持的若干基本性质,如本原性,拟本原性,幂零性等,见本文定理4。此外,本文使用的群论和特征标符号参考[17],特别指出的是,按照[11]中的记法,将用G′表示另外一个群而不是通常表示的导群[G,G]。
1 预备知识
本节给出所需的群论和特征标理论中的若干基本概念和结果。
首先引入一个技术性概念,即所谓的特征标对。考虑有限群G,称(H,θ)为G的一个特征标对,如果H为G的子群而θ∈Irr(H)。我们在G的所有特征标对构成的集合上,如此定义一个偏序关系:即(H,θ)≤(K,φ)当且仅当H≤K并且θ是φH的一个不可约分量。根据Frobenius互反律,亦等价于说φ是θK的一个不可约分量。在此情形下,称θ在φ的下方,而称φ在θ的上方。任取g∈G,令(H,θ)g=(Hg,θg),其中θg(hg)=θ(h),对任意h∈H,称(H,θ)g为(H,θ)的一个共轭。不难看出G按共轭方式作用在其所有特征标对的集合上,我们记
Gθ={g∈G|(H,θ)g=(H,θ)} ,
称为(H,θ)在G中的稳定子。显然Gθ≤NG(H),并且Gθ即为θ在NG(H)中通常的惯性群。
固定一个特征标三元组T=(G,N,θ),即N◁G,并且θ∈Irr(N)是G-不变的,我们引入若干相关的概念和符号。
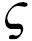
·T的截面,定义为N/Z(T),记为Sec(T)。
·T的幂零性,如果T的截面Sec(T)是幂零群,则称T为幂零的。
·T的拟本原性,如果对任意M≤N,M◁G,则θM为齐次的特征标,即θM=eφ,其中e为正整数,而φ∈Irr(M),则称T是拟本原的。
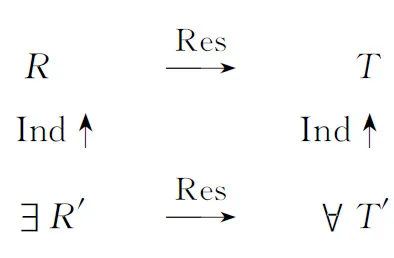
·T的本原性,如果T没有真诱导子,即不存在诱导子Τ′=(G′,N′,θ′)使得G′ 关于特征标三元组的限制子和诱导子,需要下述两个基本结论,分别称之为限制对应和诱导对应,证明可见[18]中的引理2.11。 下述群论结果是初等的,完备起见,给出一个证明。 引理3如果G为类大于2的幂零群,则G存在一个非中心的交换特征子群。 证明设G的幂零类为r,考虑G的下中心列,其中Gi=[G,…,G]共i个G做换位子: G≥G′≥G2≥…≥Gr≥Gr+1=1 . 因为r≥3,故2(r-1)≥r+1,所以[Gr-1,Gr-1]≤G2(r-1)≤Gr+1=1,表明Gr-1为G的一个交换特征子群。注意到[Gr-1,G]=Gr≠1,故Gr-1不在G的中心里,即为所求的非中心交换特征标子群。 下述为幂零的拟本原特征标三元组的一个重要性质。 引理4令T=(G,N,θ)为拟本原的特征标三元组,如果N/Z(θ)是幂零群,则N/Z(θ)为交换群。 证明因为θ是G-不变的,故Kerθ为G的正规子群。显然所给条件和所证结论可以在商群G/Kerθ中考虑,不失一般性,可设Kerθ=1。此时Z(θ)=Z(N),故N本身即为幂零群。任取A是N的一个交换特征子群,则A◁G。又因为T为拟本原的,故θA=eα为齐次的,其中e为正整数,而α∈Irr(A)。但Kerα=A∩Kerθ=1,即α为A的一个忠实的线性特征标。显然θ的G-不变性推出α亦如此,所以αg(a)=α(a),对任意g∈G和a∈A均成立,据此可知α(gag-1a-1)=1,再从α的忠实性推出gag-1a-1=1,亦即ga=ag,表明A≤Z(G)。应用上述引理,则N的幂零类不能大于2,该结论等价于说N/Z(N)为交换群。 在本节最后,还需要Dade在[6]中引入的诱导源概念。设(A,α)为G的一个特征标对,令Gα={g∈G|(A,α)g=(A,α)}为(A,α)在G中的稳定子,如果特征标的诱导 为双射,则称(A,α)为G的一个诱导源。群G-的所有诱导源的集合记为IS(G),称上述ξ为ξG的一个诱导源对应。不难看出,当A◁G时,则Clifford对应即为一个诱导源对应,从而(A,α)总是G的一个诱导源,由此表明诱导源和诱导源对应分别是正规子群和Clifford对应的一个自然和直接的推广。 类似子群的指数,需要引入子三元组的相应概念。设T=(G,N,θ)为一个特征标三元组,如果Τ′=(G′,N′,θ′)为T的一个子三元组,我们记|T:T′|=|N:N′|,称为T′在T中的指数。 在引言中提及的诱导子映射,其构造定义如下所述。 进而,该映射保持诱导子的指数不变,即|T:T′|=|R:R′|. Fig.2 Inductor and restrictor图2 诱导子和限制子 验证N′∩H′=M′且N′H′=G′。事实上,按定义有 N′∩H′=N′∩(H∩G′)=N′∩H=(N′∩N)∩H=N′∩M=M′ . 此外,从G=NH=N′MH=N′H即可推出N′H′=N′(H∩G′)=(N′H)∩G′=G∩G′=G′. 最后验证R′为R的一个诱导子,我们先证明M∩H′=M′且MH′=H。事实上,按定义M∩H′=M∩(H∩G′)=M∩G′=(M∩N′)∩G′=M′∩G′=M′。进而,使用上述所证结论N′H′=G′,我们有 MH′=(N∩H)H′=(NH′)∩H=(NN′H′)∩H=(NG′)∩H=G∩H=H. 因为上述已证(φ′)M=φ,据此即证R′为R的诱导子。进而|T:T′|=|N:N′|=|M:M′|=|R:R′| . 上述结论产生了特征标三元组的一个所谓的Mackey四边形,见图3。 Fig.3 Mackey quadrangle 图3 Mackey四边形 在实际应用中,经常需要描述该映射的像,即判别R的一个诱导子R′,何时可作为T的一个诱导子T′的限制子,亦即R′=f(T′)。在文献[16]中,曾给出了一个充分条件,即R′=(H′,M′,φ′)中的子群M′在N中正规(等价于M′◁G)。使用诱导源的概念,可将正规条件进一步减弱,故给出该文主要结果的一个推广。 定理2设T=(G,N,θ)为特征标三元组,R=(H,M,φ)为T的一个限制子。如果R′=(H′,M′,φ′)为R的诱导子,使得(M′,φ′)为N的一个诱导源,则T存在一个诱导子T′=(G′,N′,θ′),使得R′为其一个限制子。 验证T′为T的一个诱导子。因为上述已证θ′到N的诱导为θ,故T′为T的一个诱导子当且仅当NG′=G且N∩G′=N′。事实上,按定义有N∩G′=N∩G(φ′)=N(φ′)=N′。已知R为T的限制子,我们有G=NH。又R′为R的诱导子,又有H=MH′,所以G=NH=(MN′)(MH′)=N′H。显然H′固定φ′,即H′≤G′,至此有 NG′=(MN′)G′≥N′MH′≥N′H=G, 迫使NG′=G,至此即证T′为T的一个诱导子。 最后验证R′为T′的一个限制子。因为上述已证θ′到M′的限制为φ′,故只需验证N′∩H′=M′和N′H′=G′。注意到H′固定φ′,我们有 N′∩H′=N(φ′)∩H′=N∩H′=N∩(H′∩H)=(N∩H)∩H′=M∩H′=M′ . 因为H′正规化N◁G,故H′也正规化N′=N(φ′),所以N′H′为G的子群,并且包含在G′=G(φ′)中。令X=N′H′,使用模律,可知 X∩N=(N′H′)∩N=N′(H′∩N)=N′(H′∩H∩N)=N′(M∩H′)=N′M′=N′ . 同理,应用上述已证等式G=N′H,有 XN=(MN′)(N′H′)=N′(MH′)=N′H=G. 据此可知|X:N′|=|G:N|=|G′:N′|,即|X|=|G′|,但X≤G′,只有G′=X=N′H′,即证R′为T′的一个限制子。 如果T的限制子R为一个覆盖子,则所述诱导子映射恰为双射,在应用时非常便利。 定理3 设T=(G,N,θ)为特征标三元组,如果R=(H,M,φ)为T的一个覆盖子,则诱导子映射f:Ind(T)→Ind(R)为双射,并且任意诱导子T′∈Ind(T)的像R′=f(T′)∈Ind(R)也是T′的一个覆盖子。 Z(θ)∩H=Z(θ)∩N∩H=Z(θ)∩M=Z(θM)=Z(φ) , Fig.4 Restriction correspondence 图4 限制对应 最后验证R′也是T′的一个覆盖子。事实上,根据覆盖子的定义,我们有Z(θ)H=G。因为(θ′)N=θ,不难证明Z(θ)≤Z(θ′)。使用模律,我们有 G′=G′∩G=G′∩(Z(θ)H)=Z(θ)(G′∩H)=Z(θ)H′≤Z(θ′)H′≤G′ , 只有G′=Z(θ′)H′,表明R′也是T′的一个覆盖子。 下面探讨诱导子映射所保持的若干基本性质。 定理4设R=(H,M,φ)为特征标三元组T=(G,N,θ)的一个限制子,f:Ind(T)→Ind(R)为相应的诱导子映射,任取T的一个诱导子T′=(G′,N′,θ′),设R′=f(T′)=(H′,M′,φ′),则下述结论成立: (1)如果R′是本原的,则T′也是本原的。 (2)如果T′是幂零的,则R′也是幂零的。 (3)如果R′既是幂零的又是拟本原的,则T′为拟本原的。 (4)如果T′既是幂零的又是拟本原的,则R′为拟本原的。 证明(1)因为T′的诱导子显然也是T的诱导子,即Ind(T′)⊆Ind(T),而T′的诱导子对应R′=f(T′)又是T′的一个限制子,故诱导子映射f的限制f′:Ind(T′)→Ind(R′)仍为诱导子映射。因此,如果T″为T′的一个诱导子,则R″=f′(T″)也是R′的诱导子,但已知R′本原,故R″=R′,再根据诱导子映射保持指数的性质,我们有|T′:T″|=|R′:R″|=1,表明T′=T″,即T′也是本原的。 (3)根据Isaacs的一个定理,见[9]中推论2.4(b),从R′既是幂零的又是拟本原的,可知R′必然是本原的。再从结论(1)推出T′也是本原的,从而更是拟本原的。 (4)因为R′为T′的限制子,简单计,可用R和T分别替代R′和T′证明所述结论。为证R的拟本原性,按定义,任取(A,α)≤(M,φ),其中A◁H,我们只需证α为H-不变的。事实上,从T的幂零性和拟本原性,可知N/Z(θ)为交换群,故Z(θ)A◁N,表明θ在Z(θ)A上的限制是齐次的,从而在A上的限制也是齐次的。但φA包含不可约分量α,故α在θ的下方,只有θA=eα,对某个正整数e。又因为θ为G-不变的,更是H-不变的,据此推出α也是H-不变的。


2 主要结果