双种群锥面积差分进化算法求解投资组合问题

吴昱,黄晓森,巫斌,黄海南,梁浩

(1.广州大学 计算机科学与网络工程学院,广东 广州 510006;2.华南理工大学 软件学院,广东 广州 510006)

0 引言

投资者按照一定的比例,将资金分别投资在不同的股票中,以达到分散风险的目的,这种投资方式就是投资组合,而如何寻找最优的投资组合,就是对投资组合问题的优化研究。随着我国经济的高速发展,越来越多的人将节余的资金投入股票市场,以期望得到更多的收益。然而,股票投资在获得高收益的同时,往往带有极高的风险。为了使投资在收获更高收益的同时还能降低风险,找到最优的投资组合,对投资组合问题的优化研究便成了现代投资理论中一项极具价值的研究。

投资组合问题是一个典型的NP难问题[1]。在1952年,马科维茨教授首次提出了投资组合中的均值-方差模型[2],奠定了现代投资组合问题的理论基础。在理想情况下,当一个投资者需要购买N种股票,第i个股票所投资的资金在投资组合的所有资金中所占的比例为xi,其期望收益率为Ri,股票i和j的期望收益率之间的协方差为Cov(i,j),如此,均值-方差模型便可描述为:

(1)

其中E表示投资组合收益率的均值即预期的收益率,σ2表示投资组合的方差即预期的风险率。如此,对投资组合问题的求解也就转化为求一组x(x1,x2,…,xN),使得投资组合预期的收益率E最大,预期的风险σ2最小。

不难看出,均值-方差模型表示的投资组合问题是一个双目标优化问题[3],且在现实生活中的股票投资上,高收益的股票往往带有高风险,这使得均值-方差模型的两个目标相互矛盾,求解难度较大。近十几年来,随着股票种类飞速增加,投资组合问题的维度逐渐增多,较早期的解决方法已难以解决大规模股票的投资组合问题,一些启发式算法如遗传算法[4-7]、模拟退火[8-9]等新应用于投资组合问题的算法,虽能解决大规模的投资组合,但在求解速度上又不太理想。如此,差分进化(Differential Evolution,DE)算法[10-11]这一更加简单高效的进化算法便被尝试运用于投资组合问题。该算法通过模拟生物进化的随机模型,并采用基于差分的变异操作以及竞争策略,保留了遗传算法基于全局的搜索策略,有利于防止结果陷入局部最优;并且,跟遗传算法相比,DE算法受控参数少,操作简单,容易实现。

在早期,投资组合问题常常被当作双目标优化问题进行求解。在使用上述算法对其进行求解时,将得到一组趋于帕累托前沿[12]的近似最优解。然对于投资者而言,其往往希望得到的是在一定收益下的最小风险,或在一定风险下的最大收益,而不是在一组数据中寻找自己的理想组合。且双目标问题求解出来的帕累托前沿,并不是一个可以用某一函数表示的精准曲线,其求解出来的这组数据有概率并不存在投资者所希望得到的数据,这使得投资者需对该问题进行重新求解。因此,顺应大多数投资者的投资理念,也为了降低均值-方差模型的求解难度,可为投资组合中的收益率或风险设置一个限制条件,如投资者期望达到的收益率或投资者所能接受的风险,将均值-方差模型由双目标优化问题转化为单目标约束优化问题[13],在满足投资者限制条件下,求解得到一个风险最小或收益最大的投资组合。本文以投资者期望达到的收益率ER为期望收益率的限制条件,以此得到以下为单目标约束优化问题的投资组合优化模型:

(2)

式中ΔE为这种投资组合对投资者期望收益率的满足程度,当ER-∑xiRi≥0时,ΔE赋值为0,否则ΔE=ER-∑xiRi.

本文使用的是一种基于锥面积思想的锥面积差分进化算法——CADE算法[14]。在投资组合问题中,每增加一种股票,其求解的空间维度就增加一维,而差分进化算法又是通过多次迭代来求解问题的算法,随着求解空间维度的增加其求解难度也急剧增大,同时,基本差分进化算法在求解过程中,种群的多样性容易随着迭代次数的增加而变小,这对依靠种群差异来进化求解的差分进化算法来说十分致命。CADE算法则采用了双种群的搜索机制,对两个种群使用不同的更新机制,保存种群个体的有利信息,不仅保留了差分进化算法高效的特点,还在一定程度上弥补了其种群多样性随迭代次数增大而变小的缺点。

1 差分进化算法

差分进化算法是Storn等人于1995年提出的一种高效的全局优化算法,早期其被用于解决切比雪夫多项式问题,后又被用于求解复杂的优化问题。它和遗传算法一样,是基于群体的启发式搜索算法,种群中的每个个体都对应着求解问题的一个解;其进化过程也与遗传算法非常相似,都包含有杂交、变异和选择操作,但这些操作的具体定义又与遗传算法有所不同。算法主要流程如下[15]:

(1)初始化:初始化种群个体及各项参数,并对种群的个体进行评价。

(2)进行变异、交叉操作:从父种群内随机选择两个个体进行相减操作,得到一个差分值XF2-XF1;随机选择父种群中某个个体XF3与这个差分值相加求和,得到一个实验个体XF3+(XF2-XF1);再用这个实验个体与其父代个体XF进行杂交、变异操作,得到子代个体XB,如公式(3)所示;进行多次变异、交叉操作,得到子种群。

(3)选择操作:对子种群的个体进行评价,在子种群和原种群中择优选择个体,得到新种群。

(4)判断是否达到终止条件,若是,终止进化,否则,迭代次数自加,转步骤2。

DE/rand/exp算法和DE/current-to-rand/exp为两种典型的DE算法,较之一般的DE算法,他们引入了邻居的概念,在父代个体的选择上,以一定概率在父代种群中随机选择,或者在被选父代个体的邻居中随机选择。在进行变异、交叉操作时他们也有所不同,前者仅用差分值XF2-XF1与其父代个体XF进行变异、交叉操作,如公式(4)所示,而后者使用父代个体XF、差分值XF2-XF1、该父代个体XF与父种群中随机选择的某个个体XF3的差分值XF3-XF,三者进行变异、交叉操作生成子代个体XB,如公式(5)所示。

XB=XF+rate×(XF3+(XF2-XF1)) ,

(3)

XB=XF+rate×(XF2-XF1) ,

(4)

XB=XF+myrand×(XF3-XF)+rate×(XF2-XF1) ,

(5)

其中myrand与rate均为随机数。在CADE算法中,为了使算法更加稳定,其采用了由DE/rand/exp和DE/current-to-rand/exp两种典型的DE算法组成的自适应混合DE算法[16]来生成子代,其通过定义变量Ada-rate为自适应率,以此控制两个典型的DE算法被选择使用的可能性。在每一代中,变量Ada-rate的更新公式如下:

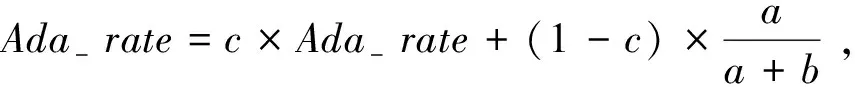
(6)

其中,a是使用DE/rand/exp算法生成个体并成功更新种群的数量,b是使用DE/current-to-rand/exp算法生成个体并成功更新种群的数量,c是一个控制参数,一般设置为0.5,计算得到的自适应率Ada-rate为使用DE/rand/exp算法生成子代的概率。一般情况下,为了避免出现只使用一个典型DE算法生成子代的情况,当自适应率Ada-rate大于0.95时,则直接把Ada-rate设置为0.95,同样的,当自适应率Ada-rate小于0.05时,直接将Ada-rate设置为0.05。

2 基于锥面积思想的CADE算法

CADE算法是由巫斌、应伟勤等人提出的基于分解思想的锥面积差分算法,其采用双种群的搜索机制来搜索最优解,采用由DE/rand/exp和DE/current-to-rand/exp两种典型的DE算法组成的自适应混合DE算法来生成子代,在双种群上采用不同的更新机制进行种群更新,不仅保留了DE算法高效的特点,还在一定程度上弥补了其种群多样性随迭代次数增大而变小的缺点。

算法的主要流程如下:

(1)初始化种群大小N,锥面积区域数量N1,最大迭代次数MAX-FES,进化代数FES=0。生成种群个体并进行评价。

(2)根据锥面积区域数量N1,对种群空间使用分区技术进行锥面积分区,并对种群个体进行区域划分与排序。

(3)使用双种群机制将种群划分为两个子种群,两个子种群的个数分别为N1和N-N1。

(4)使用自适应混合DE算法生成N个子代个体,形成子代种群。

(5)根据不同的条件对两个种群使用不同的更新策略,分别是基于锥面积比较的更新策略,基于容差排序的更新策略,基于可行性规则[17]的更新策略。

(6)判断FES是否大于MAX-FES,若是则算法结束,终止进化,得到最优值;否则FES=FES+1,转步骤2。

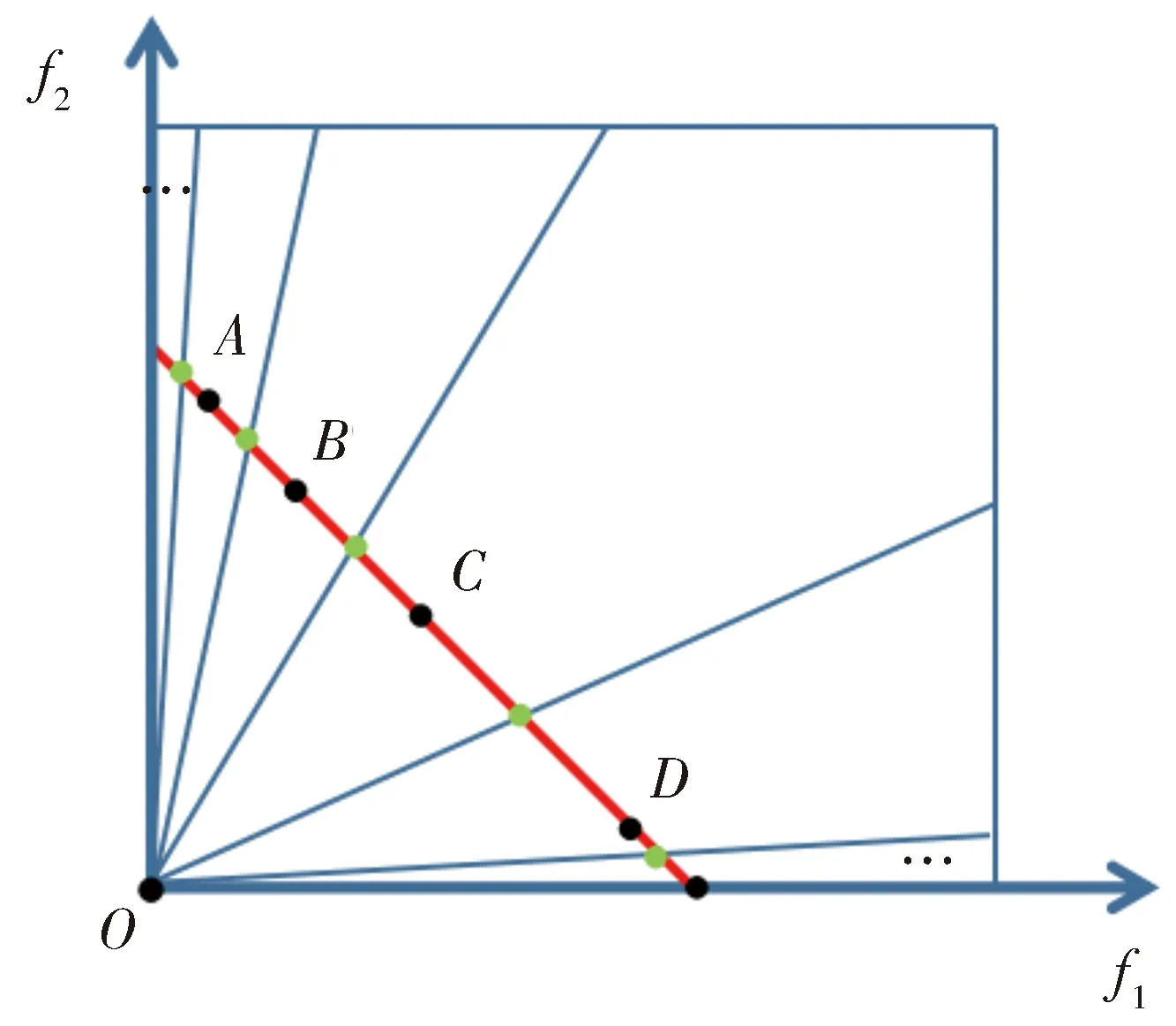
Fig.1 Conical SubregionPartition Technology图1 锥形子区域分区技术

在约束优化问题中,往往其目标函数值与约束违反程度值处于不同的数量级,且每次算法迭代更新后,种群个体在原坐标系上无法很好表现出需要的信息。因此在对种群空间进行分区前,需要对种群空间进行一定的标准化。因此本文中,将约束问题的目标函数值定义为f2,将其约束的不满足值定义为约束违反程度即f1。而在CADE算法中,其对每次迭代后的种群个体,以最小的目标函数值f2m为横坐标轴,以最小的约束违反程度f1m为纵坐标轴,即以(f1m,f2m)为原点对种群空间进行空间尺度标准化。

2.1 分区技术

2.1.1 空间分区技术

在CADE算法中对种群空间进行分区处理,采用了几何比例的偏斜锥体分解,将种群空间分解成N1个等比锥形子区域,分解方法如图1所示,于种群空间中以函数f1+f2=1取一直线,在直线上以公式(7)取一系列黑点,黑点之间的距离关系如公式(8)所示;再取每两个黑点之间的中点为绿点,从原点出发向这些绿点引出射线,将种群空间分解成N1个等比锥形子区域;省略号表示其中省略部分的点与线。其中q为等比分区的比例,s表示左边第一个黑点的横坐标的大小,k表示第k个黑点,第k个黑点所在的区域为第k个区域,其两条边界的斜率分别为公式(9)和公式(10)。

(7)

(8)

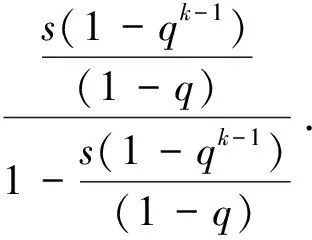
(9)

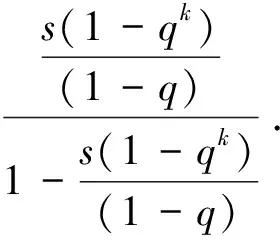
(10)

2.1.2 种群个体空间分配策略

在CADE算法中,对种群空间进行分区后,将种群的个体通过偏斜锥分解的方式计算出其所在的区域并将其分配。当区域分配到的个体不止一个时,算法对区域分配到的个体进行判断,若都属于通过偏斜锥分解法分配到该区域,则对这些个体进行锥面积比较,锥面积较优的个体留在这个区域,较差的个体则依据就近原则,寻找离这个区域的最近的没有个体的区域进行分配;若有本身不属于这个区域的个体,则将不属于这个区域的个体依据就近原则分配到离这个区域最近的没有个体的区域。偏斜锥分解的方式如图2所示:

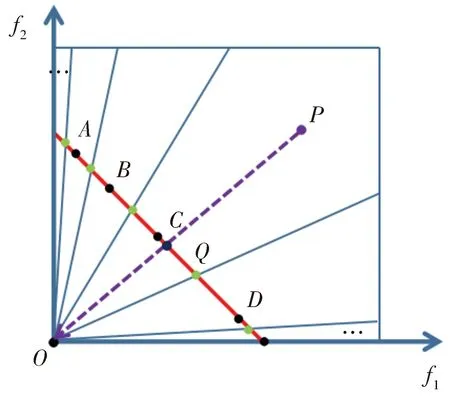
Fig.2 Deflection conedecomposition method图2 偏斜锥分解法

图2中,红线的函数为f1+f2=1,取点P(a,b)并向原点映射得一直线,与红线相交于点Q,则直线PQ的函数为f2=(b/a)*f1,则点Q的坐标为(a/(a+b),b/(a+b)),如此可根据公式a/(a+b)≤(s(1-qk))/(1-q)计算出k的最大值,得到点P所在的区域。

2.2 双种群机制

2.2.1 双种群划分策略

对于约束优化问题来说,可以将问题的解按对约束条件的满足情况分成两类,一类解为满足约束条件的或约束不满足程度小于一定值W的解,其余的解划分为另一类解。基于双种群机制的算法可以根据解对约束条件的满足情况而分为可行子种群和不可行子种群两个子种群。其中,用于判断的约束容忍值W会随着进化代数的变化而变化,以此使得算法在更新时可以渐渐逼近具有较低约束违反程度f1且较优目标函数值f2的解。其计算公式为:

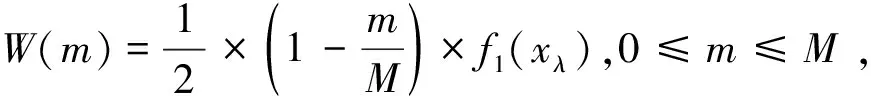
(11)

其中,xλ为存在锥面积中最后一个锥形子区域的个体,M表示算法的最大进化代数,m表示当前进化代数。

在基本DE算法中,对子代的更新策略使用的是可行性规则,即保留更优个体淘汰较劣个体,因此有了种群多样性容易变小,算法过早收敛的缺点。而在CADE算法中,其使用了双种群机制,对于两个种群采用了不同的更新策略,以此不仅在可行子种群中逐步逼近最优解,还在不可行子种群中根据个体的有价值信息寻找最优解。其图解如图3所示。

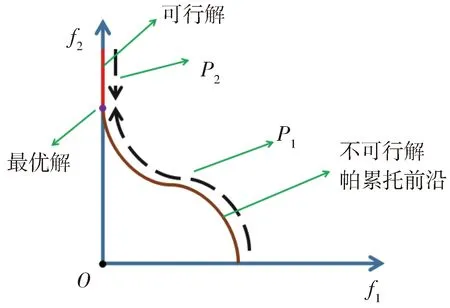
Fig.3 Double population mechanism图3 双种群机制

图3中,可行子种群P2通过不断地比较与更新,沿直线向下寻找逐步逼近最优解;不可行子种群P1则借据其有价值信息沿帕累托前沿曲线寻找最优解;其中帕累托前沿为二目标问题中不可行域映射到该前沿的最优解集,包含有不可行子种群中最有价值的信息个体。

2.2.2 双种群更新策略

CADE算法对双种群分别采用了不同的更新策略。在不可行子种群中其采用的是基于锥面积思想的更新策略,通过对锥形子区域内的个体进行比较保留较优个体,通过种群迭代找到不可行种群中的有效信息并保留在锥形子区域中,使保留的个体迫近帕累托前沿上的个体,逐渐逼近最优解。主要比较过程为:通过偏斜锥分解方式计算出子代个体所在的区域a,通过偏斜锥面积计算出区域a中的父代个体的区域b。若a=b,则对子代个体与父代个体进行锥面积比较,优胜劣汰,留下更好的个体;若a≠b,则直接使用子代个体替代父代个体。

在可行子种群上于一定代数前使用的是基于容差排序的方式进行更新种群,当到达一定代数后,种群多样性不再是算法对问题求解的主要因素后,在更新策略上基于可行性规则进行子代更新,以此寻找最优解。

2.2.2.1 锥面积计算比较

在锥形子区域中,个体的锥面积的计算方法如图4所示,根据个体Y所在的区域,取经过这个点Y且平行于f1轴的平行线交于该区域两条射线边界的两个点U1和L,垂直于f1轴交于该区域上边界的点U2,得到一个凹四边形OU2YL,则个体Y的锥面积即为OU2YL锥面的面积。

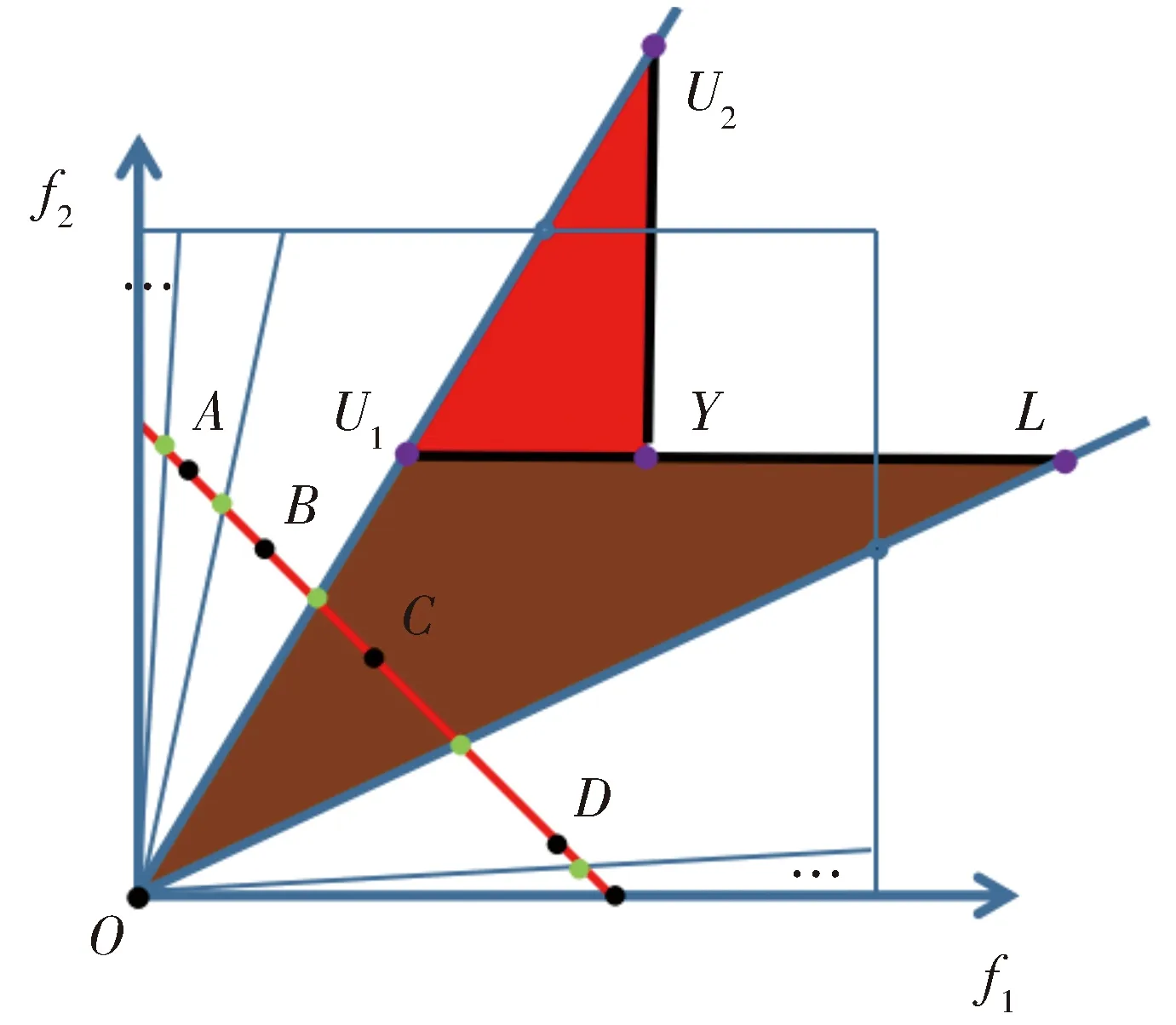
Fig.4 Cone area calculation图4 锥面积计算

根据点Y的坐标与两条射线的斜率,设Y的坐标为(a,b),U1和U2所在的射线的斜率为1/k1,L所在的射线的斜率为1/k2,则可以得知U1的坐标为(bk1,b),U2的坐标为(a,a/k1),L的坐标为(bk2,b)。

点Y的锥面积即为图中红色三角形与棕色三角形的面积和,如下公式(12)所示:

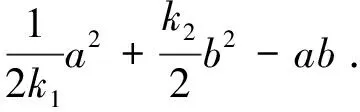
(12)

其中S为该点Y的锥面积,锥面积较小的个体优于锥面积较大的个体。

2.2.2.2 可行性规则与容差排序

基于可行性规则的更新机制较为简单,其直接表现为满足约束条件的解优于不满足约束条件的解,约束违反程度低的解优于约束违反程度高的解,都满足约束条件时目标函数值优的个体优于目标函数值差的个体。其表达式为:

容差排序,就是基于容差优势关系,给出相应的优势度量的定义,并提出基于该关系的排序方法。对于CADE算法来说,其优势度量为:约束违反程度f1满足约束容忍值W的个体优于约束违反程度f1大于约束容忍值W的个体,约束违反程度f1都满足或都不满足约束容忍值W时具有较优目标函数值的个体优于具有较差目标函数值的个体。其定义如下:

两式中,X1≤X2表示个体X1优于个体X2,f2(X1)≤f2(X2)表示个体X1的目标函数值优于个体X2的目标函数值。

3 CADE算法应用于投资组合问题

3.1 标准数据集说明

本次实验采用来源于著名的OR-Library公开的标准测试数据集,其不仅包含了投资组合问题的期望收益率,方差等数据,也提供了真实的有效解集,因此可以用来进行标准实验。该数据集包含了五个测试集,其数据主要来自世界上主要的资本市场股票数据,五个测试集的股票数量分别是31、85、89、98和225。

3.2 CADE算法实验

CADE算法实验参数说明:种群的个体数设置为300,每代更新数也为300,其中可行子种群大小为200,不可行子种群大小为100;最大迭代次数为10 000代。此外,对于自适应混合DE算法,其变异因子的取值范围[0.5,0.6],遗传因子的取值范围为[0.8,0.9]。对于投资组合问题,本算法将预估的风险即方差作为目标函数值,对期望收益率的期望程度作为约束,约束为0表示投资组合的收益率达到期望值。

在标准数据集中,期望收益率高风险高和期望收益率低风险低的分布区域中随机选择一组数据进行实验,如表1所示,表中ER为一期望收益率,而σ2表示在该期望收益率下最优,即最低的风险值,第一行数据为在期望收益率高风险高的分部区域中随机选取的,第二行数据为在期望收益率低风险低的分布区域中随机选取的。

每组数据独立进行25次实验,得到最优值best,最劣值worst与平均值average,实验结果如表2所示,从表中数据可以看出,对于port1数据集中的数据,不管是在期望收益率高风险高的分部区域还是在期望收益率低风险低的分布区域,均能满足约束条件并得到理想的风险值;对于port 2-port 5四个数据集中的数据,CADE算法在期望收益率高风险高的分部区域虽能得到理想的风险值,但其对约束条件略微有点不满足,然其不满足约束程度级数较高,误差较小;且算法在期望收益率低风险低的分布区域,不仅能满足约束条件,还得到比理想风险值略低的风险值,效果更好。

表1 实验数据

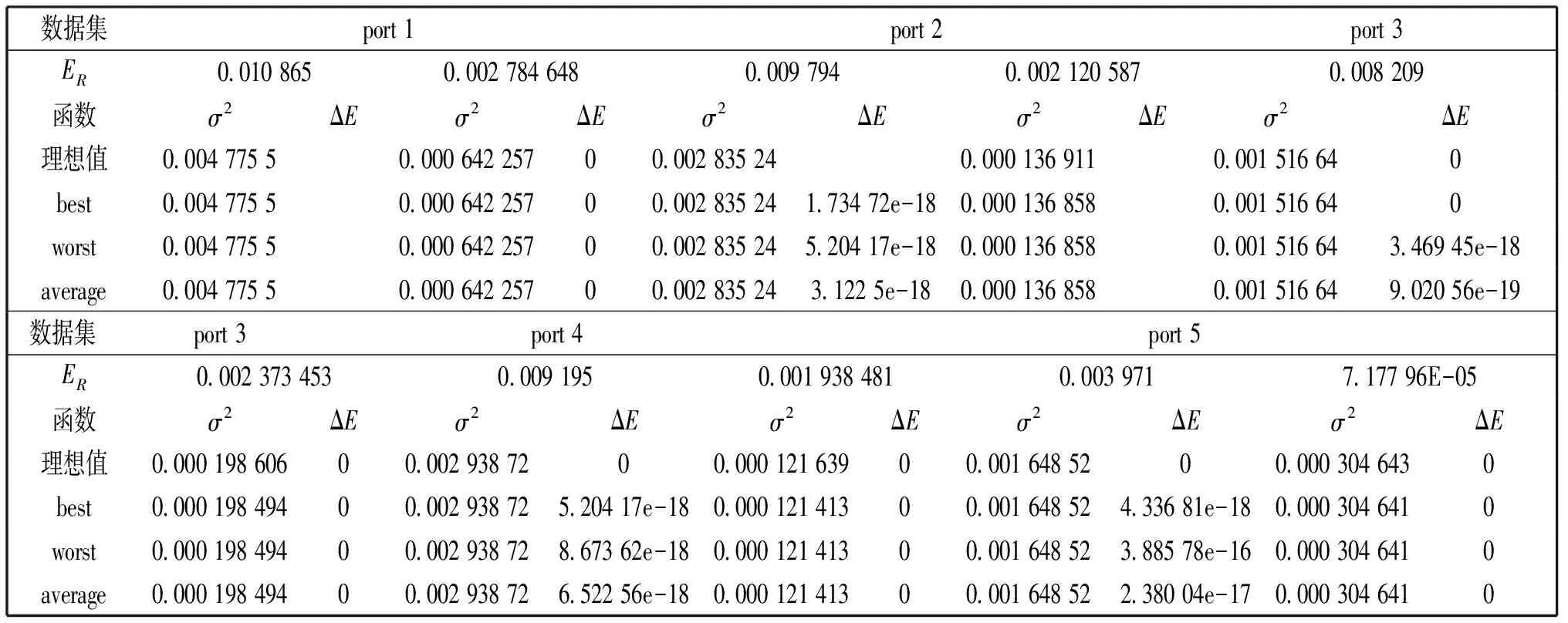
表2 CADE算法实验数据表

3.3 CADE算法与其他算法的比较

为了显示CADE算法的性能的优劣性,本文通过使用两种用于求解单目标约束优化问题的经典算法,Combining Multiobjective Optimization with Differential Evolution(CMODE)算法[18]与随机排序(SR)算法[19]对本次实验问题进行求解。在对约束优化问题的求解中,不管是单目标优化问题还是多目标优化问题,这两种算法因其操作简单,受控参数较少而被广泛运用于各个方面[20-21]。

对比实验中,在每组数据集中选取5组数据进行求解,每个算法的种群大小均为300,迭代次数均为10 000,算得最优值,最劣值与平均值,并将3个算法进行比较,结果如图5所示,图中左边纵坐标为σ2的值,右纵坐标为ΔE的值,横坐标表示各算法在当前ER期望值下的最优值,最劣值与平均值。

通过上述实验结果可以看出,CADE算法与CMODE算法在变量较少的问题上其解集质量都差不多,但当维度越来越高时可以明显看出CADE算法优于CMODE算法,特别是在期望值ER越低,风险σ2越低的地方,CADE算法可以找到甚至优于理想解,而CMODE对达到理想解还有一定的偏差,均劣于CADE算法。而对于SR算法来说,虽然其求解的解集质量较低,但随着维度越大其求解的解集质量就越好,并且某些情况,能找到好的解,如port3与port4中第五组实验;但是在大部分情况下CADE算法均明显优于SR算法。

4 结论

本文将双种群锥面积差分进化算法(CADE算法)应用于投资组合优化问题中,用来求解由经典均值-方差模型转化的单目标约束优化问题,该算法采用了双种群机制来划分投资组合优化问题中的解集,并将种群中的个体分别划分到不同的锥面积区域中,在优化过程的不同阶段对两个种群分别设计了不同的更新策略进行种群更新以维持种群多样性。通过实验并与其他算法进行比较,其结果表明CADE算法应用于投资组合上具有可行性与有效性。

在实际的投资组合问题中,还会因现实的各种因素存在着更多的约束条件,本文的后续工作则是探索如何使用更加优化的算法,求解带有更多约束条件的投资组合优化问题,以期望获得更加广泛的应用。