一类带有Hardy项的Schrödinger-Poisson系统非平凡解的存在性

李宇华,谷花

(山西大学 数学科学学院,山西 太原 030006)

0 引言

在本文中,我们主要讨论下列带有Hardy项和对数非线性项的Schrödinger-Poisson系统，

(1)

其中Ω是3中的有界光滑区域,是最佳Hardy常数。设

0<λ1<λ2≤λ3≤…≤λi≤λi+1≤…→+∞

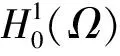
Bouchelif和Messirdi在文献[1]中考虑了含两个不同的临界Hardy-Sobolev指数的问题,他们研究下列问题

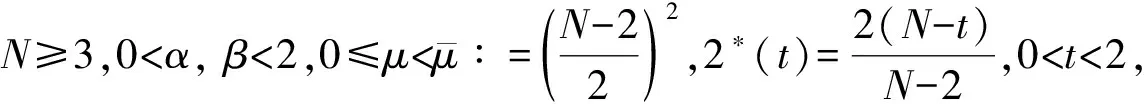
关于带有Hardy项的椭圆问题还可以参考文献[3-7]以及相关文献。另外,带有对数非线性项的椭圆问题也受到很多人的关注。例如在文献[8]中,作者研究了下列带有对数非线性项的四阶椭圆方程

的非平凡解。在文献[9]中,作者研究了一类对数Schrödinger方程

-Δu+V(x)u=ulogu2,x∈N,

他们分别获得了在势函数V可能变号和有界情形下解的存在性。另外,读者可参考文献[10-13]了解更多带有对数非线性项的微分方程问题。受文献[1]和文献[9]的启发,这篇文章的目的是获得同时带有Hardy项和对数非线性项的Schrödinger-Poisson系统非平凡解的存在性。

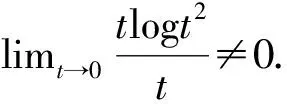
(f1)f∈C(,),而且f(0)=0;

(f3)存在C>0而且p∈(2,6)使得对于任意的t∈,|f(t)|≤C(|t|+|t|p-1);

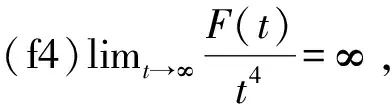
(f5)存在σ∈(0,4),及C1,C2>0使得对于任意的t∈,f(t)t-4F(t)≥C1|t|2+σ-C2t2。

我们的主要结果是:

定理1 假设f满足(f1)-(f5),则问题(1)有一个非平凡解。

1 主要结果的证明

首先,给出一些基本的记号。|·|Lq(N)表示通常的Lq(N)范数,|·|Lq(Ω)表示通常的Lq(Ω)范数且表示不同的正常数。

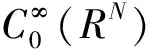
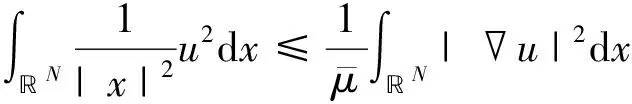
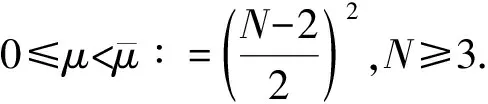
根据Hardy不等式可得

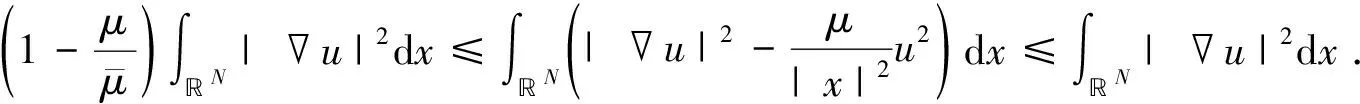
(2)

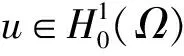
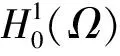
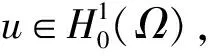
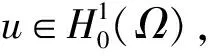
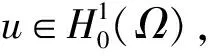
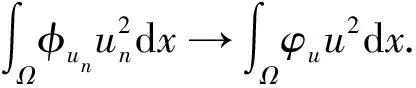
命题2 (对数Sobolev不等式[18-19]) 设u是H1(N)中任一函数而且a>0是任意一个常数,那么

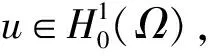
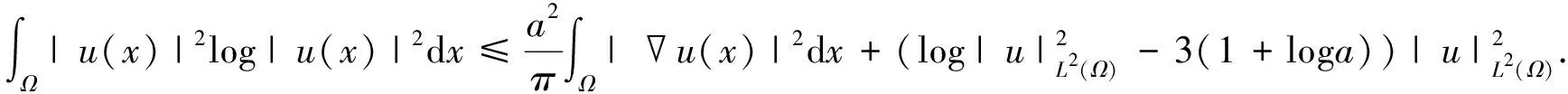
(3)

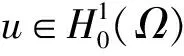
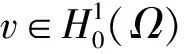
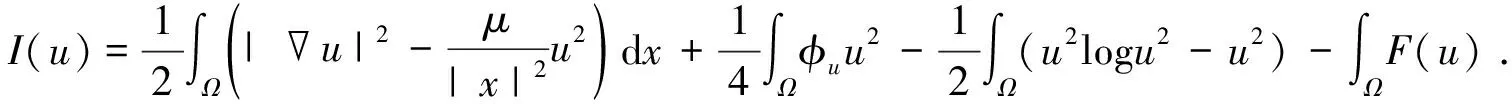
(4)

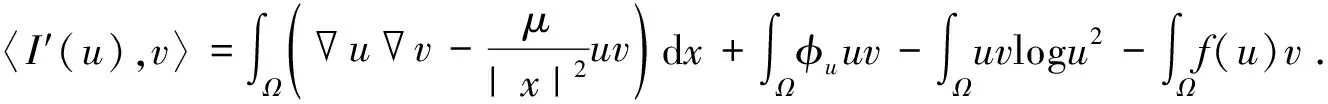
(5)

命题3(山路定理[20]) 设E是一个实Banach空间,其对偶空间为E*,I∈C1(E,),如果存在ρ>0,e∈E,且‖e‖>ρ,使得

那么存在序列{un}⊂E使得当n→∞时,

I(un)→c, ‖I′(un)‖E*→0 .

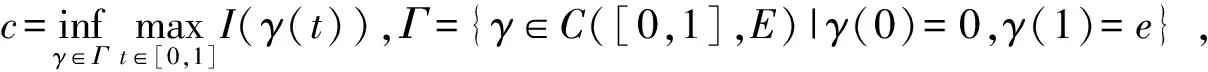
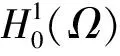
引理2 存在ρ>0以及α>0,使得inf‖u‖=ρI(u)≥α成立。

证明根据(f2),(f3),对任意给定的ε>0,存在Cε>0使得对于任意的t∈,

|F(t)|≤ε|t|2+Cε|t|p.

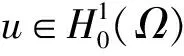
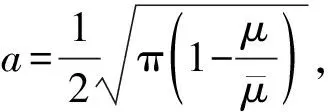
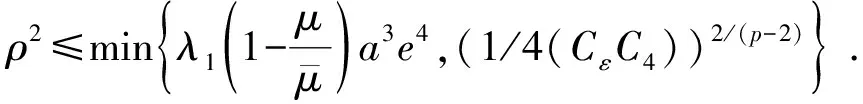
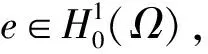
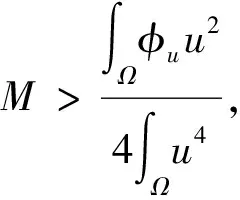
很显然,当t→+∞时,I(tu)→-∞.取e=t1u,其中t1充分大,我们有I(e)<0.

引理2与引理3表明I满足山路结构,为了得到结果,我们需要下列引理。

引理4I(u)满足(PS)条件。

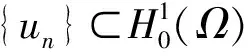
根据条件(f5),存在R>0,当|t|>R时,f(t)t-4F(t)≥C1|t|2+σ-C2t2≥t2logt2.根据f的连续性,存在C7>0使得f(t)t-4F(t)≥C1|t|2+σ-C2t2≥t2logt2-C7,t∈.所以我们有

(6)

2|unlog|un|-ulog|u||L2(Ω)|un-u|L2(Ω)→0 ,

(7)

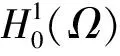
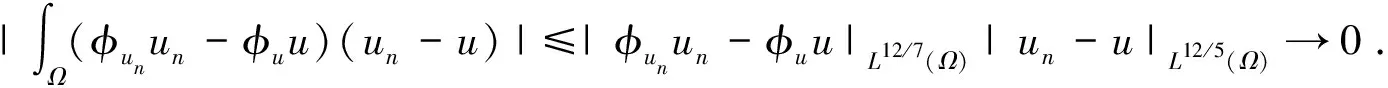
(8)

由条件(f3)及Nemytskii算子的性质可得

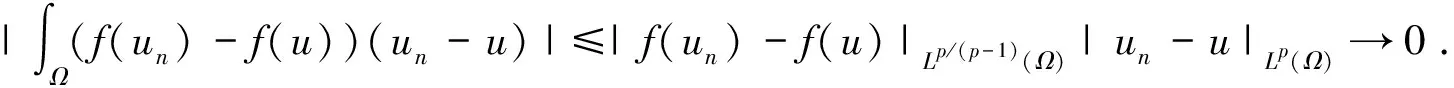
(9)

从而根据(7),(8),(9),我们有

〈I′(un)-I′(u),un-u〉=〈I′(un),un-u〉-〈I′(u),un-u〉=

另外由I′(un)→0以及弱收敛的定义可得当n→∞时,〈I′(un)-I′(u),un-u〉→0,所以‖un-u‖→0.引理得证。