一类连续型随机变量函数密度的求法

王开永，崔永芳

(苏州科技大学 数理学院，江苏 苏州 215009)

1 连续型随机变量的函数是否为连续型的问题及新的简单反例提出

在概率中，对于连续型随机变量，密度函数比，可以完全刻化连续型随机变量。在实际处理问题时，往往会碰到要处理连续型随机变量的函数分布问题，即Y=f(X)的分布问题，其中，X为连续型随机变量；f(x)为一实函数。首先要处理的问题是，连续型随机变量的函数还是不是连续型，即Y=f(X)还是不是连续型随机变量。一般情况下，没有肯定的回答。很多文献也给出了反例，例如文献[1]的例1及例2。本文给出两个新的简单反例。

例1 设X为连续型随机变量，分布函数为FX(x)=P(X≤x)，且存在实数a＞0，使得FX(a)＞0。设实函数其中IA(x)为集合A的示性函数，即，则Y的分布函数为由于FY(y)在y=0处不连续，所以，Y=f(X)不是连续型随机变量。

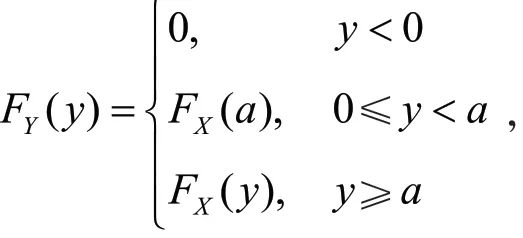
下面给出另一个反例，其中函数f(x)在(0，1)上为连续函数。先给出两个引理，第一个引理可见Embrechts等[2]的Proposition A1.6.

引理1 设G(x)是一概率分布函数，对G定义广义逆函数为

则：

(1)G-1(y)是单调不降的；

(2)y≤G(x)，当且仅当G-1(y)≤x；

(3)G(x)严格增，当且仅当G-1(y)为连续函数。

当G(x)严格单调时，G的广义逆函数G-1(y)就是通常意义下的G的反函数.下面的引理可见Rolski等[3]的Theorem 3.1.2，事实上，由上述引理1的(2)很容易给出证明。

引理2 设F(x)为一分布函数，F-1(y)为F(x)的广义逆函数。随机变量X～U(0，1)，则Y=F-1(X)的分布函数为F(x)。

证明：设Y的分布函数为FY(y)，则由引理1的(2)及X～U(0，1)可知，对任意实数y，

下面给出另一个反例。

例2 设Φ(x)为标准正态分布函数，任意取实数x1＜x2，由于Φ(x)严格单调递增，则取。定义

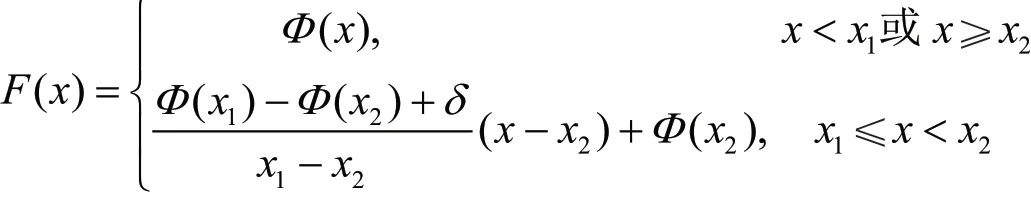
从而，F(x)为右连续，且为严格递增的函数，0＜F(x)＜1且故F(x)为一分布函数。但由于F(x)在x=x1处不连续，所以，F(x)不是连续型随机变量的分布函数。取函数f=F-1，则由引理1的(3)知f在(0，1)上为连续函数。设随机变量X～U(0，1)，则Y=f(X)=F-1(X)为连续型随机变量X的函数。但由引理2知Y=F-1(X)的分布函数为F(x)。从而，Y=f(X)不是连续型随机变量。

2 连续型随机变量的密度函数问题及改进后一般公式的提出

设X是一连续型随机变量，密度函数为pX(x)，设y=f(x)为一实函数，若Y=f(X)为连续型随机变量，则要讨论Y=f(X)的密度函数。对此，没有一个一般的公式，但对一些特殊性质的函数f(x)可以给出Y=f(X)的密度函数的计算公式。一般教材都讨论了f(x)为严格单调的情形，给出了密度函数计算公式。文献[4]、文献[5]对于f(x)不是严格单调时，给出了密度函数计算公式。很多文献讨论了f(x)为分段严格单调的情形，得到文献[5]、文献[6]的结果。

定理1 设X是一连续型随机变量，其密度函数为pX(x)，( -∞, +∞) 被分割成有限个或可列个互不相交的区间Bk(k=1，2，…)，且函数y=f(x)在Bk(k=1，2，…)上严格单调，并在Bk上其反函数x=gk(y)有连续导函数，则Y=f(X)为连续型随机变量，其密度函数为

对于上述结果，现给出以下说明：①事实上，上述分割不一定要对全体实数分割，只要对pX(x)不等于零的地方分割即可；②上述分割不一定要分割成区间，分割成一般的不相交的子集也可；③在(2.1)中，没有说明y的取值范围，有的文献默认为( -∞, +∞ )，有的文献给出了y的范围，即，其中，α为f在Bk(k=1，2，…)端点值的最小值，β为f在Bk(k=1，2，…)端点值的最大值。这些表示都不太准确，事实上，在此定理中，对每一个给定k=1，2，…，gk(y)的定义域只能是函数y=f(x)在Bk上的值域，因而，将y的范围写成( -∞, +∞) 或(α，β)是不够准确的。对此，顾玉娣[7]给出了一个例子，说明利用式(1)有时会得到错误的解。分析发现，文献[7]所举的例子在计算过程中有错误，因此不能以此例来说明(2.1)会得到错误的解。而分析定理1发现，式(1)表达不够准确，为此，本文给出一个严格的形式。

例3 设随机变量ξ～U(-1，2)，求η=ξ2的密度函数。

文献[7]的具体解法如下：

由ξ～U(-1，2)知其密度函数为

若利用公式(1)求解，y=x2在(-1，2)上不单调，将区间(-1，2)分成(-1，0]和(0，2)，y=x2的反函数分别为，从而由(2.1)知η的密度函数为

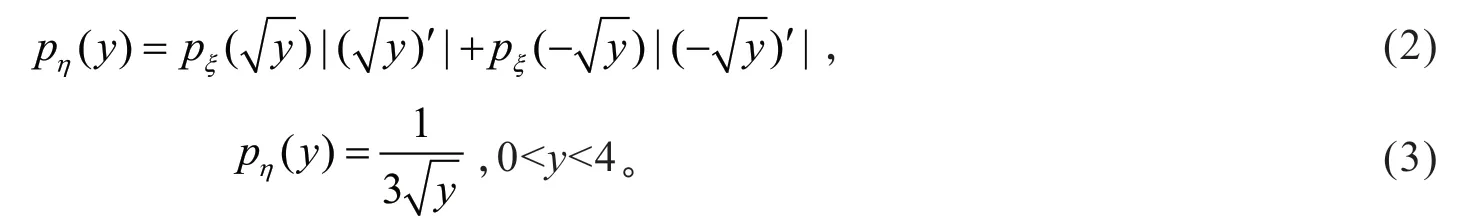
这与用“分布函数法”求出的密度函数不同，

从而文献[7]说“用式(1)得出的结果(3)是错误的”。从而，文献[7]得出的观点认为“式(1)必须加上一定条件才能成立，否则会导致错误结论”。

本文认为“式(1)是不成立的”结论存在问题。事实上，会发现在上述计算过程中，从式(2)到式(3)这一步计算是不正确的，而在上述过程中，仅式(2)这一步使用了式(1)，而式(2)到式(3)这一步并不使用式(1). 从而，上述例子不能说明式(1)是不成立的。下面说明在上述计算过程中，从式(2)到式(3)是错误的。

事实上，当y≤0或y≥4时，由式(2)及pξ(x)的表达式知pη(x)=0；当0＜y＜4时，从而。故，式(2)等于如下：

从而，由式(5)知

这与用“分布函数方法”求出的式(4)一致。因此，本文认为式(1)表述不严格。下面给出定理1一个严格的形式，对于实函数y=f(x)，x∈( -∞, +∞ )，对任意集合B⊆( -∞, +∞ )，称为B在f下的逆象；称为B在f下的象。容易证明，对任意集合当y=f(x)在B上严格单调时，有反函数x=g(y)，则

定理2设X是一个连续型随机变量，其密度函数为p X(x) ，记a=inf{x:p X(x) ＞ 0}，b=sup{x:p X(x) ＞ 0}，(-∞≤a＜b≤+∞)。设区间(a，b)被分割成(有限个或可列个)互不相交的子集Bk，(k=1，2，…)，且函数y=f(x)在Bk，(k=1，2，…)上严格单调，且在Bk上其反函数x=gk(y)有连续导函数。记Ck=f(Bk)，则Y=f(X)为连续型随机变量且其函数密度为

证明：当y≤α时，Y的分布函数FY(y)=0，所以pY(y)=0；当y≥β时，FY(y)=1，pY(y)=0。我们讨论α＜y＜β的情形，此处证明(a，b)被分割成可列个子集的情况，有限个类似，即。当x∈Bk时，设。先求Y的分布函数FY(y)，

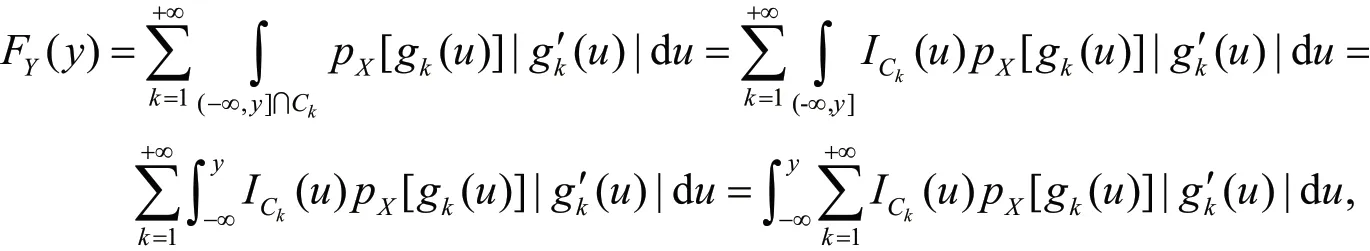
从而，Y的密度函数为

由定理2，可以得到下面两个常见函数的密度函数。

推论1 设X是一个连续型随机变量，其密度函数是pX(x)。若(-∞≤a＜b≤+∞)，则

1)Y=|X|也为连续型随机变量，

当b≤0时，其密度函数为

当a＜0且b＞0时，其密度函数为

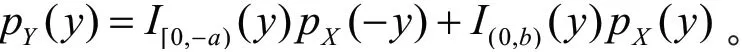
当a≥0时，其密度函数为

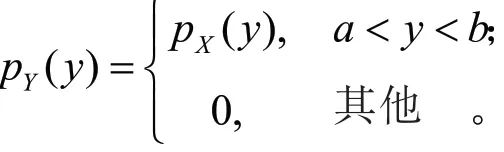
2)Y=X2也为连续型随机变量，

当b≤0时，其密度函数为

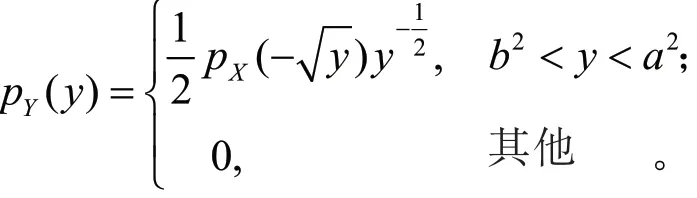
当a＜0且b＞0时，其密度函数为

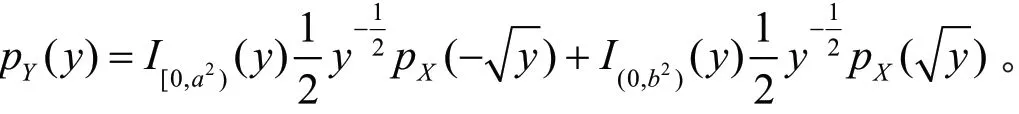
当a≥0时，其密度函数为

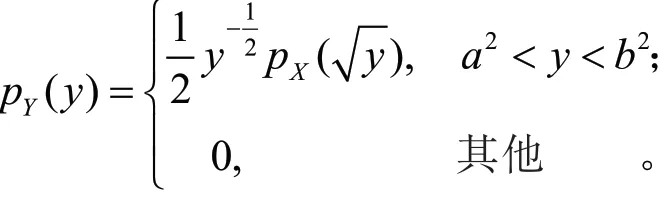
对于上述例3，很容易由推论1得到如下正确结果。

将(-1，2)分成B1=(-1，0]和B2=[0，2)两个区间，可知C1=[0，1)，C2=[0，4)，y=f(x)在B1，B2上的反函数分别为。所以由推论1容易得到

3 结论

从连续型随机变量的函数是否为连续型随机变量这一问题出发，讨论了相关情形，并给出了连续型随机变量的函数不为连续型随机变量的例子。对于其中一类情形，即当函数为分段严格单调时，对连续型随机变量的函数的密度给出了一般计算公式。