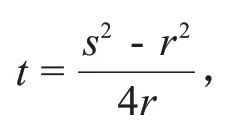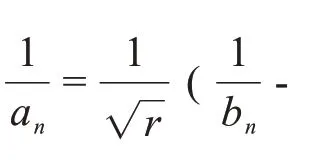多项式数列的连续分解
赵凤鸣
(四川职业技术学院 应用数学与经济系,四川 遂宁 629000)
我们将文[1]第83 页第14 题作为本文的引例,该题如下:
在文[2]中,作者给出的解法如下:
解

故 原式
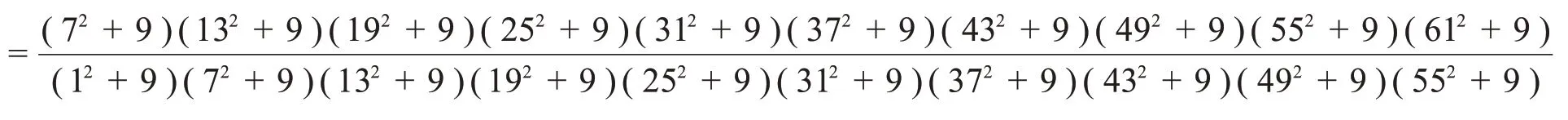

我们认为,可以对该解法进行优化,给出一个较为一般实用的方法。注意到等差数列

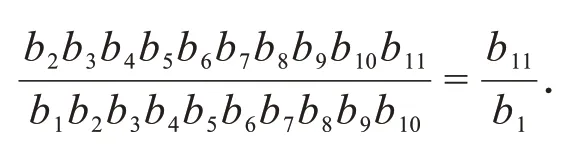

从上面的分析可以看出,研究数列an是否能分解为an= bnbn+1显然具有重要意义,这样的分解我们就称为数列的连续分解。一般,我们给出如下的
定义对于数列an,若存在数列bn,使an= bnbn+1…bn+k-1(k ≥2),则称bnbn+1…bn+k-1是数列an的一个k 阶连续分解。
由于问题的复杂性,我们在这里不做一般的研究,只研究an是n 的次数不超过4 的一些特殊多项式的这种分解,并假设bn也是n 的多项式.显然,若an是一次多项式,则研究an的连续分解没有意义,所以假设an分别为2,3,4 次多项式。对于an为2 次和4 次多项式的情形,显然研究an的2 阶连续分解才有意义,而对于后者的一般性研究显然很困难,这里只研究an为形如( rn + s )4+ t 和rn4+ sn2+ t 的4 次多项式.对于an为3 次多项式的情形,显然研究an的3 阶连续分解才有意义,一般性研究显然很困难,不过也可以对an的某些特殊情况进行研究,但限于篇幅,本文在这里不作研究。
定理1设四次多项式an= ( rn + s )4+ t,r >0,若存在多项式bn,使an= bnbn+1成立,则r4= 4t,并且若假设bn的首项系数大于0,则
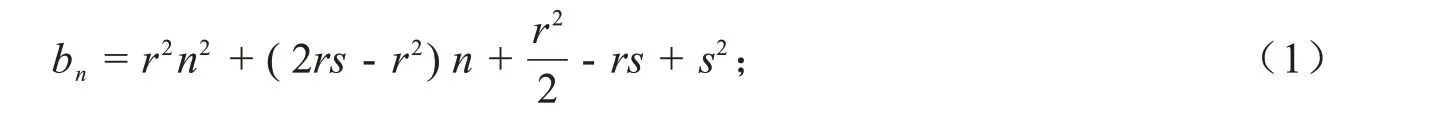
反之,若r4= 4t,则(1)满足an= bnbn+1.
证明:若存在多项式bn使an= bnbn+1成立,因bn和bn+1是同次多项式且首项系数相同,则bn必为二次多项式,设bn= an2+ bn + c,有
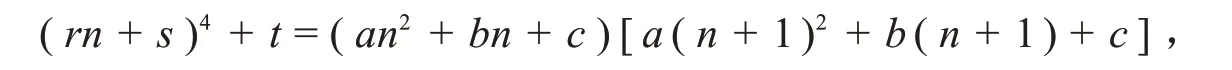
因此不妨设a >0.上式即为

比较系数得

由(A)前四式解得

将a,b,c 代入(A)的最后一式得r4= 4t,将a,b,c 代入代入bn= an2+ bn + c 得(1).

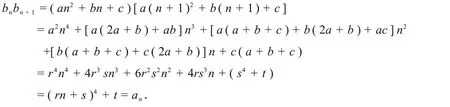
在引例中,r = 6,s = -2,t = 324,满足r4= 4t,由定理1 可直接求得bn.由于以下定理2 和定理3 的证明类似于定理1 的证明,故略.
定 理2设 四 次 多 项 式an= rn4+ sn2+ t,若 存 在 多 项 式bn,使an= bnbn+1成 立,则r >0,( r + s )2= 4rt,并且若假设bn的首项系数大于0,则

反之,若r >0,且( r + s )2= 4rt,则(2)满足an= bnbn+1.
如计算: