对均值不等式的认识

李凤清，张子卫，张青山

（四川职业技术学院，四川 遂宁 629000）

教师要合理选择数学材料，从观察、数学感觉形成入手训练学生的数学眼光，引导学生用数学的眼光看世界[1,2]；运用基本的数学概念、数学事实与数学结论，从策略、方法、能力三个方面训练学生的数学思维，学会用数学的思维分析世界；从数学思想的感受与数学价值的体现建立学生的数学情感，用数学的语言表达世界，培育学生的数学核心素养.

由二元均值不等式到三元均值不等式，再到n 元均值不等式，我们觉得这个问题很有意思.这里有知识的迁移与深化，还有认识的加强与跃迁，更有情感与态度的固化.

三元均值不等式的等价形式：

若a,b,c ＞0，则a3+ b3+ c3≥3abc.

或者：a,b,c ＞0，且abc = 1，则a + b + c ≥3.

n 元 均 值 不 等 式：对n 个 正 数a1,a2,…,an，其 几 何 平 均不 大 于 其 算 术 平 均

其等价命题为：对乘积为1 的n 个正数a1,a2,…,an，必有a1+ a2+ … + an≥n.

1 运用基本数学概念认识均值不等式

由平均值这个概念可知，一个数组的平均值总不会大于这个数组中的最大数，也不会小于这个数组中的最小数.

（1）显 然，a,b 两 个 正 数 的 几 何 平 均 必 介 于a,b 之 间，故，即 可 得

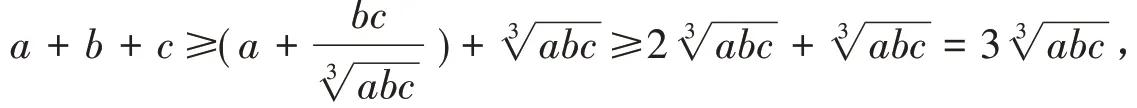
（3）对n + 1 个正数a1,a2,…,an,an+1，其几何平均必介于这n + 1 个正数的最小数（不妨设为a1）与最大数（不妨设为a2）之间，故，即可得

2 基本数学方法的使用

2.1 逐步调整法

逐步调整法是数学中的基本方法.弄清调整的过程与调整后所产生的变化，并依此继续调整下去，获得最终的结论.

下面我们把上面的认识过程数学化.

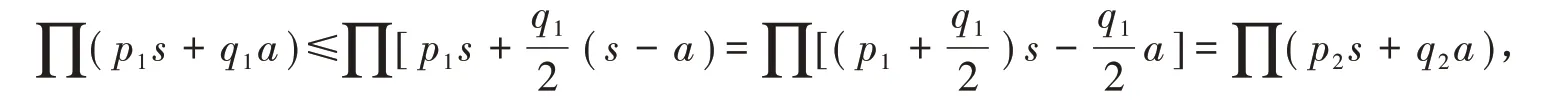
设n 是正整数，那么就有

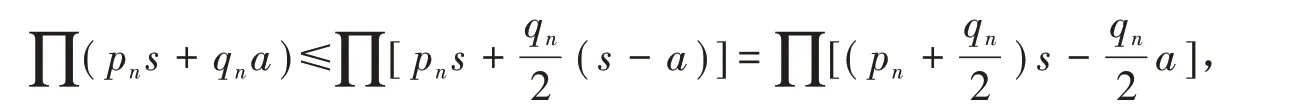
记

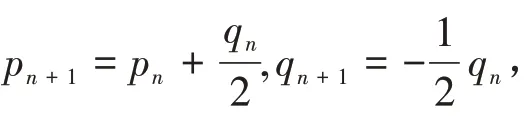
那么对任意正整数n，均有

当n →+∞时

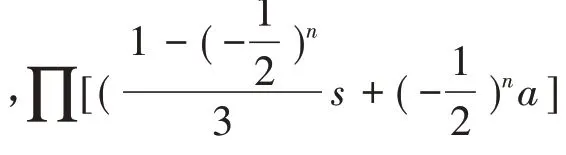
若对任意n 个正数，其算术平均不小于几何平均，那么对n + 1 个正数a1,a2,…,an,an+1，记s = a1+a2+ … + an+ an+1，那么就有

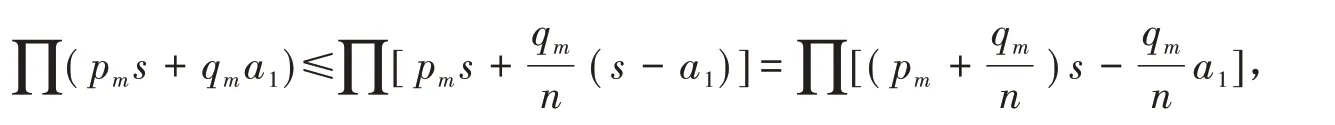
2.2 主元法

欲证a3+ b3+ c3- 3abc ≥0，在三元三次齐次多项式a3+ b3+ c3- 3abc 中，以c 为主元，由于

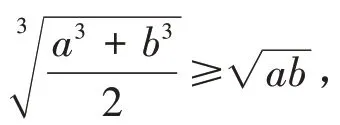
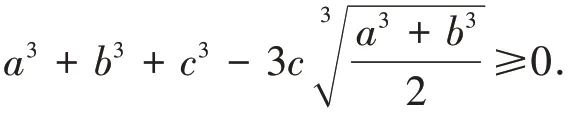
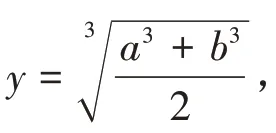
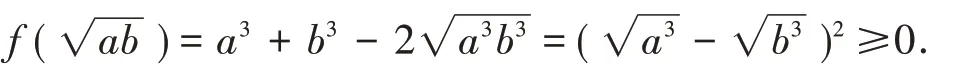
同 理，欲 证

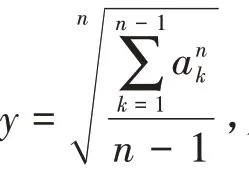
当然也可以用导数的方法来解决.

2.3 使用常见不等式x ≥1 + lnx( x ＞0 )

如

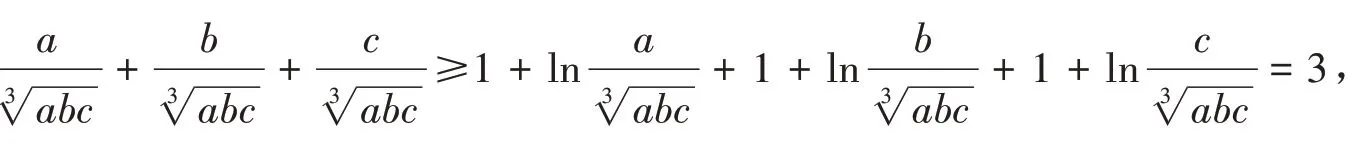
运用上面方法很容易证明算术几何平均不等式.

2.4 构造函数

同理有

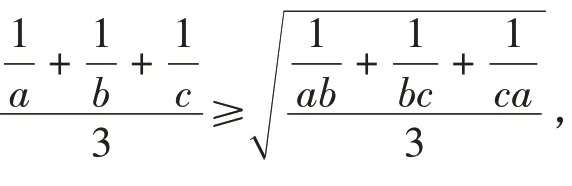
等价于

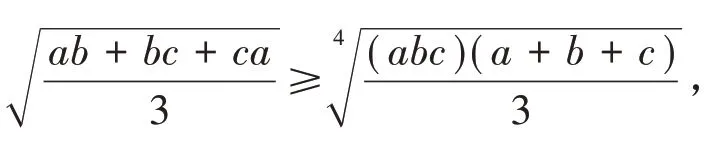
运用这个方法可以推广到多元均值不等式.

3 基本策略的使用

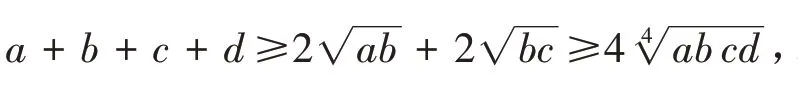
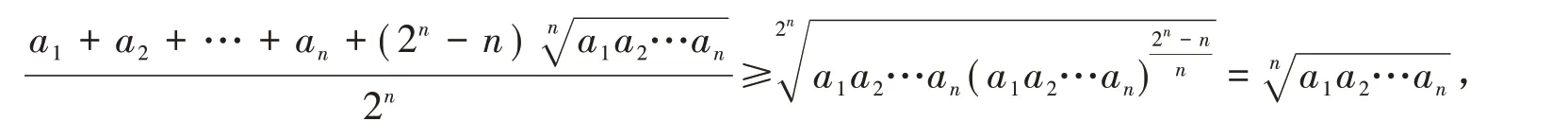
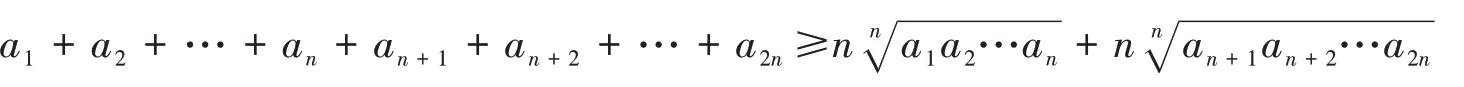
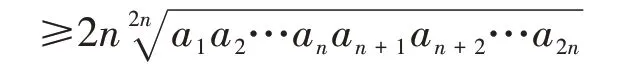
由以上阐述我们认识到，基本概念、基本方法、基本策略是数学核心素养的灵魂.运用基本概念、基本方法、基本策略来认识数学知识，解决数学问题是培养数学核心素养的关键.