浅谈初中数学中线段最值的求解策略

◎叶彬

线段最值问题的题型灵活、多变，是初中生较难解决的问题之一，也是棘手问题。这类试题都是立足于教材，能在教材找到基本的原形，如两点之间线段最短、垂线段最短、三角形两边之和大于第三边、轴对称、旋转等。解决问题的途径，通常需要运用转换思想，将较为复杂的问题转换为常见的基本类型，从而找到解决问题的基本思路。下面，笔者将结合具体的实例，谈谈初中数学中线段最值的求解策略。

一、利用“垂线段最短”求最值

例 1.如图 1，在 Rt△AOB 中，∠AOB＝90°，∠A＝30°，OB＝3，以 O 为圆心，半径为1作⊙O，P是线段AB上一动点，过点P作⊙O的切线交⊙O于点Q，求线段PQ的最小值。

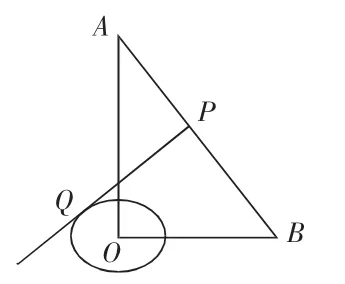
图1

分析：在 Rt△AOB 中，∠AOB＝90°，∠A＝30°，OB＝3，可得。因为PQ是⊙O的切线，所以，根据圆的切线性质作辅助线：连接OQ，则OQ⊥PQ，再连接OP，就可以组成一个直角三角形，如图2，由勾股定理可知，OP2＝PQ2＋OQ2，由于 OQ 为定值，因此，当 OP 取得最小值时，PQ 也取得最小值。而点O是一个定点，点P是线段AB上一动点，当OP⊥AB时，OP取得最小值。此时，由三角形面积法可得，解得，，再由OQ＝1得，，所以，PQ最小值是。

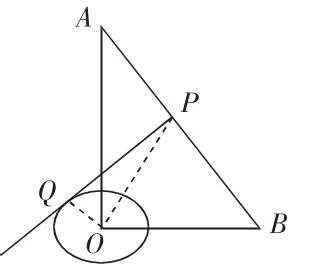
图2

小结：题目求解的切入点是利用圆的切线性质构造直角三角形，由勾股定理将“求PQ的最小值”转换为“求OP的最小值”，也是将问题转换为“垂线段最短”问题。求解过程中运用了圆的切线性质、勾股定理、面积法求高、垂线段最短等知识点，将上述相关性质结合，就可以变为解题的法宝。

二、利用轴对称性质求最值

例2.如图3，在平面直角坐标系中，∠OAB＝90°，点A在x轴正半轴上，点B的坐标为，点C的坐标为，斜边OB上有一个动点P，求(PA＋PC)的最小值。

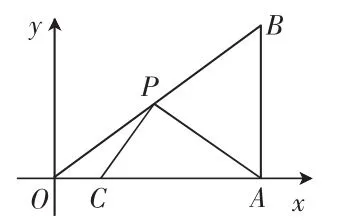
图3

分析：由图3观察可知，点A和点C是两个定点，点P是OB上的动点，求(PA＋PC)的最小值。很明显，这是求“最短路径”问题中的同侧问题，因此，可以利用轴对称性质解决问题。

如图4，以OB为对称轴，作点A的对称点D，连接CD交OB于点P，此时，(PA＋PC)取得最小值，且PA＋PC＝PD＋PC＝CD。所以，只要求出 CD的长即可。

过点D作DN⊥OA，交于OA于点N，在Rt△OAB和Rt△DNA中，

因为，∠DAN＋∠DAB＝∠DAB＋∠ABO＝90°，

所以，∠DAN＝∠ABO，即∠ADN＝30°

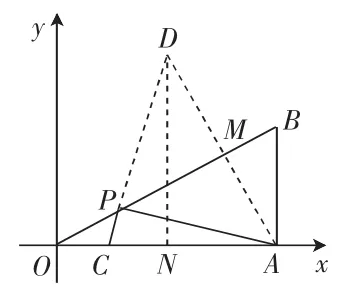
图4

小结：图形经过轴对称变换之后，会产生的等量关系(线段相等、角相等)，合理地利用相应的性质会使问题得到简化，这会给解题带来很大的帮助。本题中是作直线的对称点，实现直线同侧点到异侧点的转化，这是我们在解题中经常遇到的情况以及常见的解题方法。

三、利用三角形的三边关系求最值

例3.如图5，∠MON＝90°，矩形ABCD的顶点A，B分别在边OM，ON上。当点B在边ON上运动时，点A随之在边OM上运动，矩形ABCD的形状保持不变，其中AB＝2，BC＝1，运动过程中，求点D到点O的最大距离。

图5

分析：如图 6，取线段 AB 的中点 E，连接 OE、DE，此时，OD、OE、DE 组成一个三角形，根据“三角形的任意两边之和大于第三边”可得：OD＜OE＋DE；当矩形ABCD在移动变换过程中，存在一种特殊情况：O、D、E三点共线，这时，OD＝OE＋DE。综上可得，OD≤OE＋DE。所以，当 O、D、E 三点共线时，点D到点O的距离最大。

图6

小结：题目求解的关键在于选取一边的中点，构造一个新的三角形，利用三角形的三边关系得出不等关系式，从而找到最值。