浅谈高中数学中图示列举分析的思想方法

◎ 管尚忠

图示列举分析法就是根据数学对象本质属性的相同点与不同点，选取适当的标准，根据对象的属性，不重复、不遗漏地进行分类来解决问题的一种数学方法。数学中的一些题型通过渗透图示列举分析的方法，可启发和培养学生思维能力。笔者在此利用“类比数形结合”的思想介绍一种有利于发展教学思维、培养学生能力的典型形式——图示列举分析法的数学思想。

一、用图示列举分析法进行讨论的思想方法

1.为何使用图示列举分析法

许多数学问题由于受到某些因素的限制，例如概念的不同，性质的不同等，不能按照统一的方法、标准和公式进行处理。因此有些问题我们可以选择图示列举的方法进行分析讨论。如数学中的某些概念、定理、性质、法则、公式是分类定义或分类给出的，在运用它们时可以适当地加以图示列举分析。这样可以树立划分意识，训练思维的严谨性，保证解题的正确与完整。

2.灵活运用图示列举分析的思想方法

(1)可通过“补集”间接求解；

(2)有条件时，减少分类寻求整体解决。

二、图示列举分析法在高中数学中的应用

1.推理中的图示列举应用

例如：甲、乙、丙、丁四位学生一起去向教师询问数学竞赛的成绩。教师说“：你们四人中有2位优秀，2位良好，我现在给甲看乙、丙的成绩，给乙看丙的成绩，给丁看甲的成绩。”看后甲对大家说“：我还是不知道我的成绩。”根据以上信息，则谁可以知道自己的成绩？

解：可以图示分解如下：

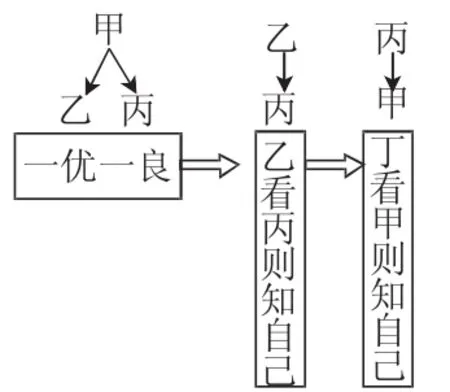
由题意知甲说不知道自己成绩即他看的乙丙一优一良，意味着甲跟丁也是一优一良。所以，乙和丁知道自己的成绩。

2.映射和计数原理中的图示列举分析

例如：已知集合 A={a1，a2，a3}，集合 B={b1，b2}，则集合 A 到集合 B 能构成多少个不同的映射？

解析：如图示：

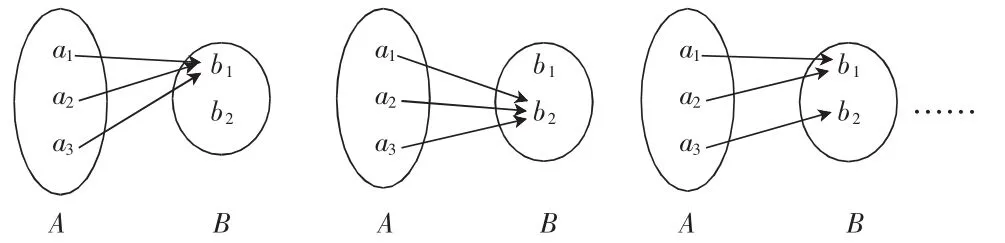
集合A中的每个元素在B中都有2个不同的的对应关系，所以由分步计数原理得 N=2×2×2=23=8。

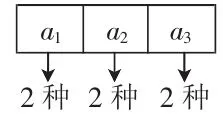
由此，通过列举和图示可知，由A中的元素选择对应B中的元素，我们可以得出一般性的结论：若一辆公交车上有n个人，途经m个站点，则他们总共不同的下车方式有：N=mn种。即把结果看成是幂的形式，其中主选元素的个数作为指数，被选的元素个数作为底数。

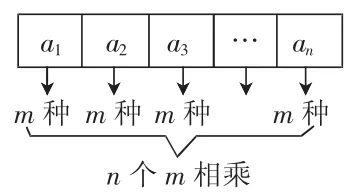
则把这种计数原理归纳为：人选车站计数原理应用：某人有3个不同的电子邮箱，他要发5封电子邮件，则发送的方法种数为N=35=243。(看作：5封电子邮件选择3个邮箱发送)

3.排列组合等问题中的图示列举分析

有约束条件的排列组合问题，通过图示列举，问题变得更简单、思路更清晰。

例如：由1，2，3，4，5，6组成没有重复数字的六位数，且1，3都不与5相邻的六位偶数共有多少个？

解析：依题意，按照题中的特殊元素1，3，5进行恰当地划分为两类：如图示一类：1，3相邻，但它们不与5相邻(1，3相邻作为一个元素与5插空)有

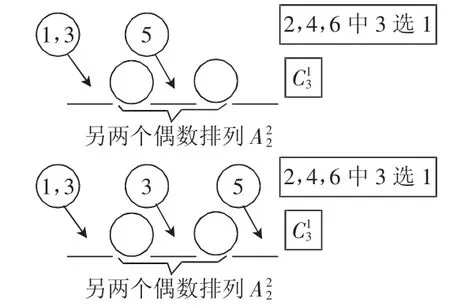
二类：1，3，5 三个都不相邻(1，3，5 三个元素插空)有

∴六位偶数共有N=N1+N2=108(个)

4.在综合信息的题型中寻求图示列举分析的方法解决

纵然在高考中会给出一些信息综合题，但都离不开使用已学习过的知识点进行推理，加以图示列举的分析使问题简单化，起到事半功倍的效果。

例如：定义“规范01数列”{an}如下：{an}共有2m项，其中m项为0，m项为1，且对任意k≤2m，a1，a2，……，ak中0的个数不少于1的个数。若m=4，则不同的“规范01数列”共有多少个？

解析：依题意，{an}共有2m项，其中0的个数与1的个数各占一半。即当 m=4 时，a1，a2，a3……，a7，a8中 0 的个数与 1 的个数各有 4 个，且必有 a1=0，a8=1。

分析：①首项为0，末项为1，留中间六个空位可以一字排如图示：

②考虑 a1，a2，a3不符合要求的，如

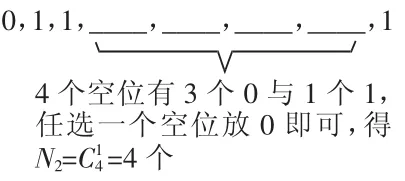
③考虑 a1，a2，a3，a4，a5不符合要求的，如下图示，又因为 a8=1，故 a6，a7只能为0，即N3=2个

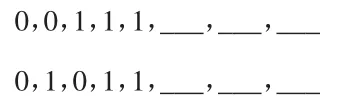
所以“，规范01数列”共有N=N1-N2-N3=20-4-2=14种。

数学题目是非常灵活的，做数学题时最重要的是学会方法。所以，笔者在这里阐述的图示列举分析思想方法，也是针对在解决数学问题中遇到的困难而提出的。其实很多种方法都是融会贯通、相互渗透的，虽然有时候图示列举分析思想方法也不一定是最好的办法，但有些题目可能通过图示列举分析思想方法会使复杂问题更加简单化。当然，最重要的是懂得活学巧用，具体问题具体分析，这样做起来才会不吃力，才会游刃有余，使困难的数学问题变得更加容易。