基于整形器的UHPC材料SHPB试验数值模拟与分析
任 亮 ,何 瑜 ,王 凯
(1.华东交通大学 土建学院,南昌 330013;2.康涅狄格大学 土木与环境工程学院,斯托尔斯康涅狄格州 06269)
超高性能混凝土(Ultra High Performance Concrete,UHPC)是一种新型的水泥基材料,具有强度高、韧性大、耐久性能优异等特点,在海上结构、地下空间、核废料容器和核反应堆防护罩等特殊工程和国防军事工程中具有广阔的应用前景。为适应其对抗冲击和抗爆性能的需求,不少学者从应变率和材料组分角度出发,通过分离式霍普金森压杆(Split Hopkinson Pressure Bar,SHPB)试验对其冲击压缩性能开展研究,结果表明UHPC动态力学性能指标随着应变率的增加而提高,适量的钢纤维掺入对UHPC材料动态增韧效果明显,但试验结果的准确性非常依赖于实验过程中的恒应变率加载和试件的应力平衡[1-4]。目前对于传统混凝土材料,已有的研究表明在SHPB试验中应用波形整形技术可有效解决上述问题[5-6]。UHPC作为一种新型建筑材料,考虑到在SHPB试验中应用波形整形技术的研究相对较少,如参考传统混凝土材料来选取整形器参数实现恒应变率加载和试件的应力平衡,其适用性和可靠性仍有待深入研究。
针对上述问题,本文采用数值分析的方法,从整形器的选择出发,应用LS-DYNA软件对UHPC材料应用整形器实现恒应变率加载和试件应力平衡的途径开展研究。通过对KCC损伤模型中材料参数取值进行优化,拟合UHPC动态损伤行为,建立了基于SHPB技术的UHPC材料冲击压缩数值模型,并与实验验证。在此基础上,开展不同整形器在材料、厚度和直径下的参数分析,探讨其对SHPB实验中恒应变率加载和试件应力平衡的影响。
1 SHPB装置
SHPB设备主体结构包括撞击杆、入射杆、透射杆和吸收杆,附属设备包括发射装置、测速装置、缓冲装置、应变片、信号放大器、电子示波器和计算机等,如图1所示。当撞击杆撞击入射杆时,高强度冲击产生一个压缩应力波,称之为入射波,入射波穿过入射杆向试件传播。当入射波到达入射杆和试件的接触面后,一部分应力波反射回入射杆,称之为反射波,剩下的部分穿过试件进入透射杆,称之为透射波。入射波信号(εI)和反射波信号(εR)可由粘贴在入射杆上应变片记录,透射波信号(εT)通过粘贴在透射杆上应变片记录。试件的应力和应变根据应变片记录的数据进行计算。

(1)
(2)
(3)
εI(t)+εR(t)=εT(t)
(4)
式中:C0表示应力波在压杆中的弹性波速,L表示试件的初始长度,A和AS分别表示压杆和试件的截面面积,E表示压杆的弹性模量,εI(t)、εR(t)和εT(t)分别表示由应变片测得的入射波、反射波和透射波信号。

图1 分离式霍普金森压杆实验装置Fig.1 Test device of split hopkinson pressure bar
为保证式(1)~式(4)成立,在SHPB试验中需满足四个前提:① 应力波一维传播;② 忽略端面摩擦效应;③ 试件应力平衡;④ 恒应变率加载。其中,应力波的一维传播可通过杆件一定的长径比来满足[7],端面摩擦效应的影响可通过端面涂抹凡士林等润滑剂来减少,而实现恒应变率加载和试件应力平衡是传统SHPB试验面临的最大挑战。这是由于传统SHPB实验中获得的入射波通常是如图2所示的梯形波,相对于其他加载波形,梯形波上升沿持续时间短(通常小于应力波在试件两个端面之间来回传播3到4次后达到应力平衡的时间)且伴随高频振荡[8],导致应变率剧烈波动,通常难以实现恒应变率加载和试件应力平衡。考虑到SHPB试验中恒应变率加载和试件应力平衡的实现与入射波的上升持续时间和波形密切相关,理想的入射波应具有一定的持续时间且上升平缓。为此,可在传统SHPB装置的撞击杆和入射杆之间放置一个可变形的软质材料作为波形整形器,当撞击杆高速撞击入射杆时,整形器通过塑性变形将原梯形入射波转化成了类似三角形的入射波(图2),从而提高波形的上升段持续时间。

图2 SHPB实验整形前后入射波对比Fig.2 Comparison of the incident wave in SHPB test before and after pulse shaping
2 波形整形效果评价指标
为评估波形整形后实现恒应变率加载的效果,本文将有效加载时间内应变率相对于平均应变率的偏离定义为恒应变率因子(Constant Strain Rate Factor,CSRF),将CSRF作为恒应变率加载的评价指标(如图3所示),相应的表达式为
(5)
(6)

从式(5)和式(6)可以看出,CSRF值越小,表示整形器修正入射波实现恒应变率加载的效果越好,根据文献[9]试验结果,一般认为CSRF不大于30%时,可实现恒定应变率加载。
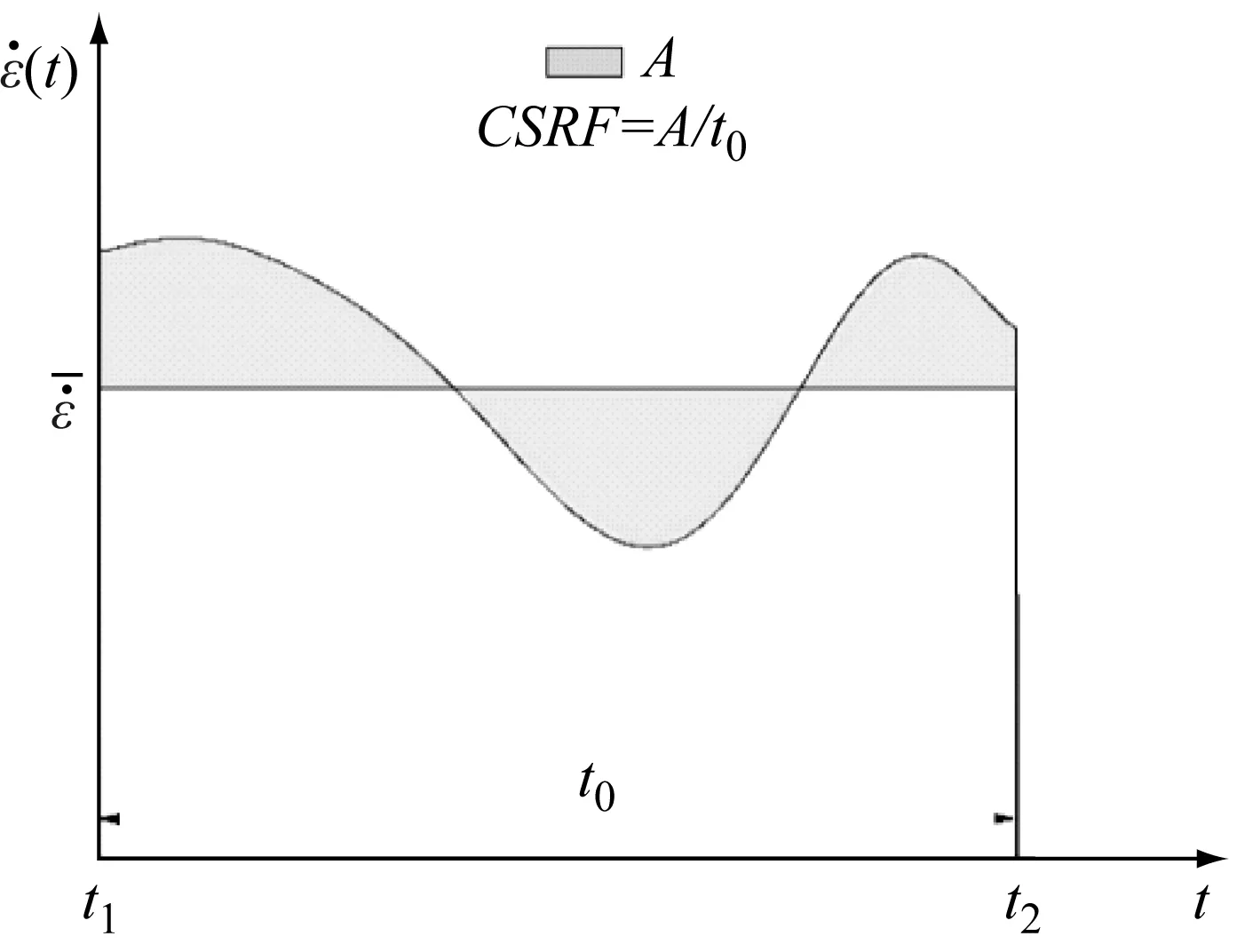
图3 恒应变率加载的定义Fig.3 Definition of constant strain rate factor
对于整形器实现试件应力平衡的评价标准,本文引入应力平衡因子D来衡量,相应的表达式为
(7)

从式(7)可以看出,D值越趋近于零,试件两端的应力越均匀,通过整形器实现试件应力平衡效果越好。
3 数值模拟
目前可用于固体非线性动力有限元分析的软件包括LS-DYNA、ABAQUS、MSC/DYTRAN、AUTODYNA等,其中LS-DYNA软件为用户提供了诸如Holmquist-Johnson-Cook(HJC)、Karagozian-Case-Concrete(KCC)等能反映材料从加载至破坏全过程力学行为的损伤模型,而被广泛应用于混凝土材料SHPB实验数值模拟中[10-11]。相对于HJC模型,KCC模型更适合模拟中高等应变率下混凝土材料的动态力学性能,且能够准确的捕捉材料在冲击荷载作用下的非线性行为,重现混凝土类材料在冲击荷载作用下真实的力学行为[12]。考虑到UHPC动态损伤模型鲜见相关的文献报道,本文应用已有的UHPC冲击试验结果,通过优化KCC损伤模型给定的参数,拟合UHPC的动态损伤行为。
3.1 KCC模型
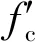
KCC模型代表的材料本构行为描述如下:应力首先上升到屈服点Pt.1,到达初始屈服面;随后材料进入强化阶段,上升到峰值强度点Pt.2,到达最大屈服面;最后材料发生破坏,下降到残余强度点Pt.3,到达残余应力面,此时材料完全破坏。三个剪切面对应的表达式为
(8)
(9)
(10)
式中:Δσy、Δσm、Δσr分别表示初始屈服强度、最大屈服强度、等效残余强度;a0y、a1y、a2y、a0、a1、a2、a1f、a2f为常量,一般通过单轴和三轴实验确定。

(a)剪切破坏面

(b)单轴应力应变关系图4 KCC模型的剪切破坏面及单轴应力应变关系Fig.4 Shear failure surfaces and uniaxial stress-strain relation in KCC model
当材料应力介于三个剪切面之间时,当前应力的计算公式为
Δσ=
(11)
式中:η(λ)表示损伤函数,λ为等效塑性应变,λm为等效塑性峰值应变,在KCC模型中η(λ)和λ以数组形式由用户输入。当λ从0增大到λm时,η(λ)由0增加到1,表示材料进入屈服强化阶段,随后η(λ)随着λ值的继续增大而逐渐下降为0,表示材料进入破坏阶段。
与此同时,KCC模型在使用时必须结合状态方程来描述混凝土的抗压性能,KCC模型使用Tabulated-Compaction模型作为状态方程,相应的加载压力和体积应变之间的关系如下
p=C(εv)+γT(εv)E
(12)
式中:εv表示体积应变,γ是温度常数,C(εv)为εv对应的体积压力值,T(εv)为εv对应的温度值,E为初始单位体积的内能,p为加载压力。
上述状态方程中加载压力随体积应变的增大单向递增;当状态方程出现卸载时,相应的卸载刚度定义为卸载体积模量K,卸载以截止压力作为终点;再加载路径沿卸载曲线加载至卸载开始点,然后按状态方程骨架曲线继续加载。在KCC模型中压力p、体积应变εv和卸载体积模量K需要用户以数组形式输入。
3.2 基于UHPC的KCC模型参数校准
对于传统混凝土,用户只需要输入一个静态抗压强度,KCC模型就可以自动生成上述参数,并能较好的模拟其力学行为。然而,UHPC材料性能与传统混凝土存在明显差异,由KCC模型自动生成的参数偏差较大,为准确模拟UHPC的损伤行为,需要对KCC模型中相关参数进行校准,其中的关键是如何拟合UHPC不同围压下的受压本构关系,以确定控制剪切面的8个主要参数,参数校准具体步骤如下。
(1)考虑到UHPC不同围压下的受压本构关系鲜有相关文献报道,参考Ali Khajeh提出的混凝土不同围压下的受压本构关系[13],对UHPC不同围压下的受压本构关系进行拟合,其中上升段为
(13)
(14)
(15)
C=A-2,D=B+1
(16)
式中:f和ε分别表示应力和应变;fpl为比例极限强度,按抗压强度的0.45倍取值;α1为初始弹性模量E0与峰值割线模量Es的比值;f0和ε0分别表示考虑围压下的峰值应力和峰值应变,其中E0,Es,f0和ε0分别由下式确定
(17)

(18)
(19)
(20)

不同围压下抗压本构下降段为
(21)
式中:frp表示受压残余应力;fic表示UHPC下降分支上拐点处的应力;εi表示考虑围压下UHPC下降分支上拐点处的应变,其中frp,fic和εi分别由下式确定
(22)
(23)
(24)
(25)
(26)
(27)
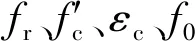
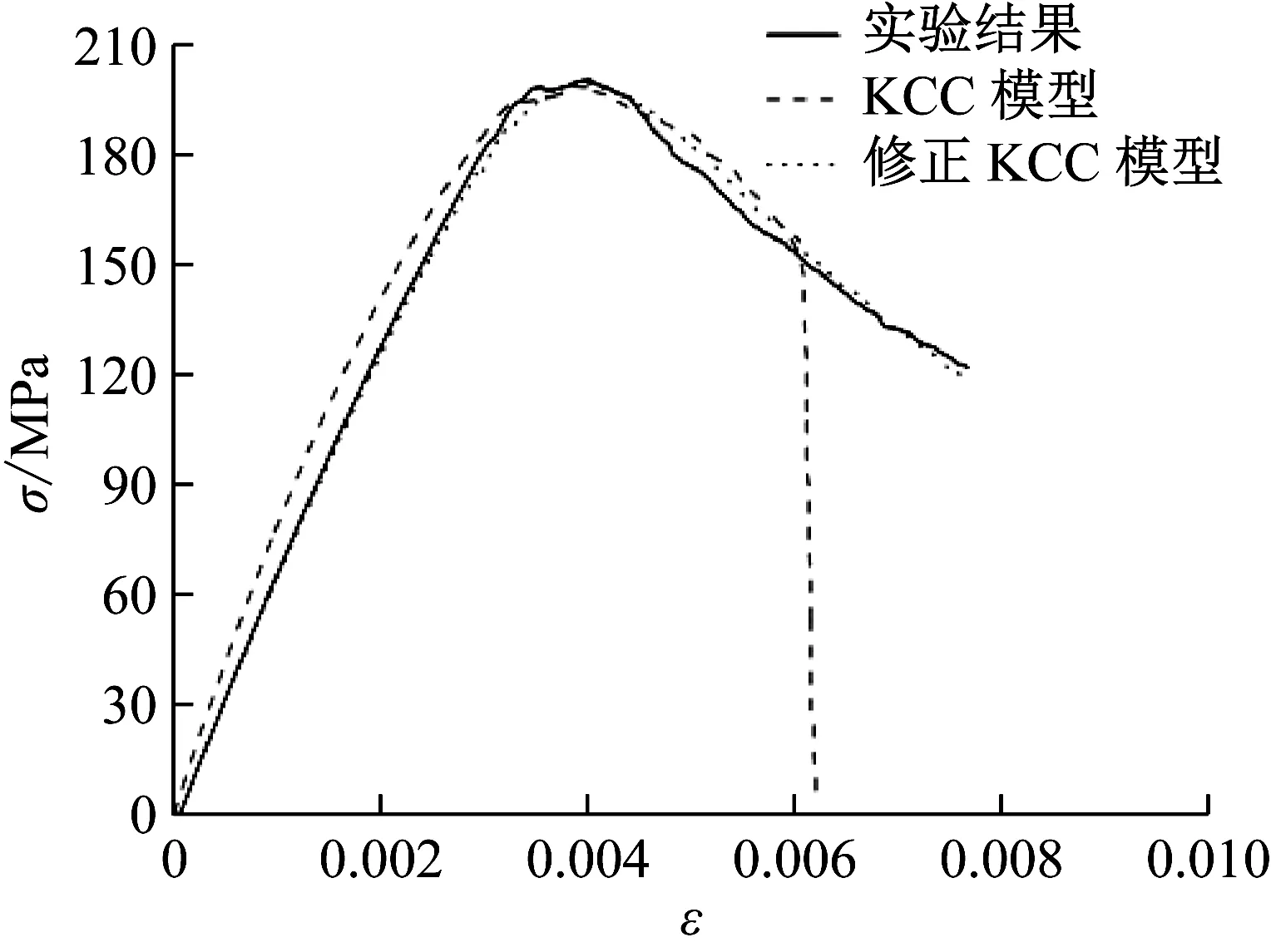
图5 UHPC本构关系拟合值与实验值对比Fig.5 Comparison of constitutive relation of UHPC between fitted values and experimental value

图6 不同围压下的应力-应变曲线Fig.6 Stress-strain curves under different confining pressure
(2)根据不同围压下的UHPC受压应力-应变曲线,可分别获得其等效屈服强度、等效破坏强度和等效残余强度点所对应的轴向应力σ1围压σ2和σ3,故主应力差Δσ和静水压力P为
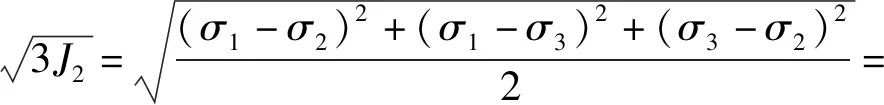
|σ1-σ2|
(28)
(29)
由式(28)和式(29)分别求出不同约束条件下对应的Δσ和P值,通过数值拟合即可得到如图7所示的三个剪切破坏面。

图7 剪切破坏面拟合Fig.7 Fitted shear failure surfaces
(3)根据图7以及式(8)~式(10)可计算得到剪切破坏面8个确定参数,如表1所示。
(4)确定损伤方程和状态方程
KCC模型中损伤方程参数η、λ以及状态方程中P、εv和K参考文献[14-15]取值,具体如表2所示。

表1 剪切破坏面确定参数Tab.1 Parameters for determining the shear surfaces
3.3 数值仿真模型
应用大型有限元程序LS-DANA建立了如图8所示的SHPB数值仿真模型(为节省计算时间和占用的空间,模型中应用对称性仅选取截面的四分之一进行建模)。其中杆件、整形器和UHPC试件均采用三维solid164实体单元,UHPC材料损伤模型选用参数校准后的KCC模型,整形器选用Plastic-Kinematic模型(各向同性、随动硬化或两者混合的模型)考虑材料的塑性变形。试件和整形器单元网格按横向5 mm、纵向1 mm划分,杆件单元网格按横向5 mm、纵向20 mm划分,在杆件与试件、杆件与整形器接触部分单元,为防止负体积的产生,杆件单元纵向网格细分(长度为1 mm),以保证模拟结果的准确性。所有界面接触均采用自动面面接触(Automatic Surface-to-Surface),且不激活静/动态摩擦系数,以排除端面摩擦效应的影响。
3.4 实验验证
基于上述数值仿真模型,本文对文献[9]中实测的无整形器和有整形器两种情况下的入射波、反射波和透射波分别进行数值模拟。试验中整形器材料选取铝,其厚度和直径分别为2 mm和10 mm,相应的材料参数如表3所示;UHPC试件长度和直径分别为9.2 mm和23.8 mm,相应的静态抗压强度为200 MPa;SHPB设备中杆件特征参数如表4所示,撞击杆速度为10 m/s。图9为实测波形和计算波形的对比。
从图9可知,整形器使用前后试验曲线和模拟曲线大致吻合。相对于未使用整形器波形,SHPB试验在使用整形器后入射波有明显的上升平台,且透射波取得峰值前,反射波有一段近似保持水平,数值模拟中较好的反映了波形的这种变化,说明本文提出的数值仿真模型有较好的精准性。

表2 损伤函数和状态方程Tab.2 Damage function and equation of state
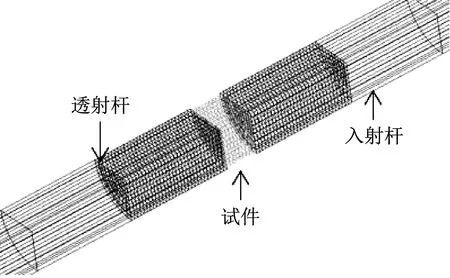
(a)试件接触部位

(b)整形器接触部位图8 SHPB数值仿真模型Fig.8 Numerical model of SHPB

表3 整形器材料参数Tab.3 Material parameters of Pulse Shapers
4 参数分析
基于上述数值分析方法,本文选取整形器的材料、直径和厚度等关键参数,对UHPC试件在SHPB实验中应用整形器的效果进行分析。分析时SHPB装置、试件尺寸和UHPC静态抗压强度与实验验证中取值一致。
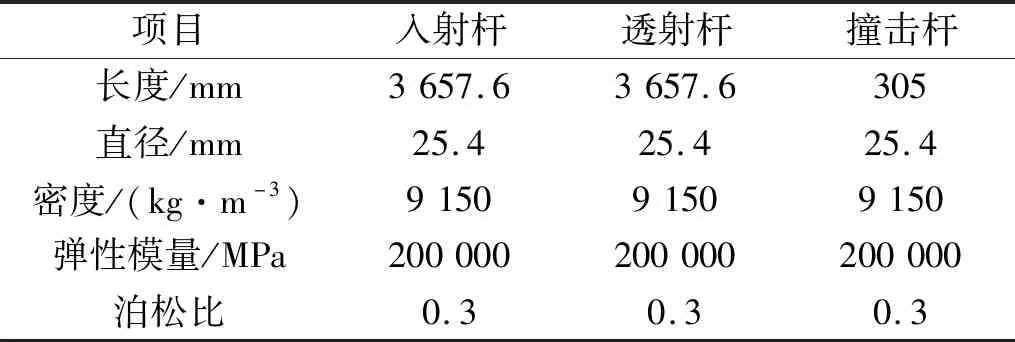
表4 杆件的特征参数Tab.4 Characteristic Parameters of Bars

(a)未使用整形器

(b)使用整形器图9 试验波形与计算波形对比Fig.9 Comparison of the waveforms between experiment and calculation
4.1 整形器材料
为探讨整形器材料的影响,在保持整形器厚度2 mm不变的情况下,分别对铜质和铝质整形器的整形效果进行分析对比,如图10所示(图中铜用Cu表示,铝用Al表示)。分析时整形器的直径分别取6 mm、8 mm和10 mm。
从图10(a)中可以看出,未设置整形器时,SHPB装置在加载过程中恒应变率因子CSRF值达到69%,在使用整形器后CSRF值明显降低且均小于30%的临界值,表明整形器是实现恒应变率加载的有效途径;在整形器尺寸相同情况下,相对于铜质整形器,铝质整形器能获得的更小的CSRF值,意味着铝质整形器对入射波的修正效果优于铜质整形器,能更好的实现恒定应变率加载。
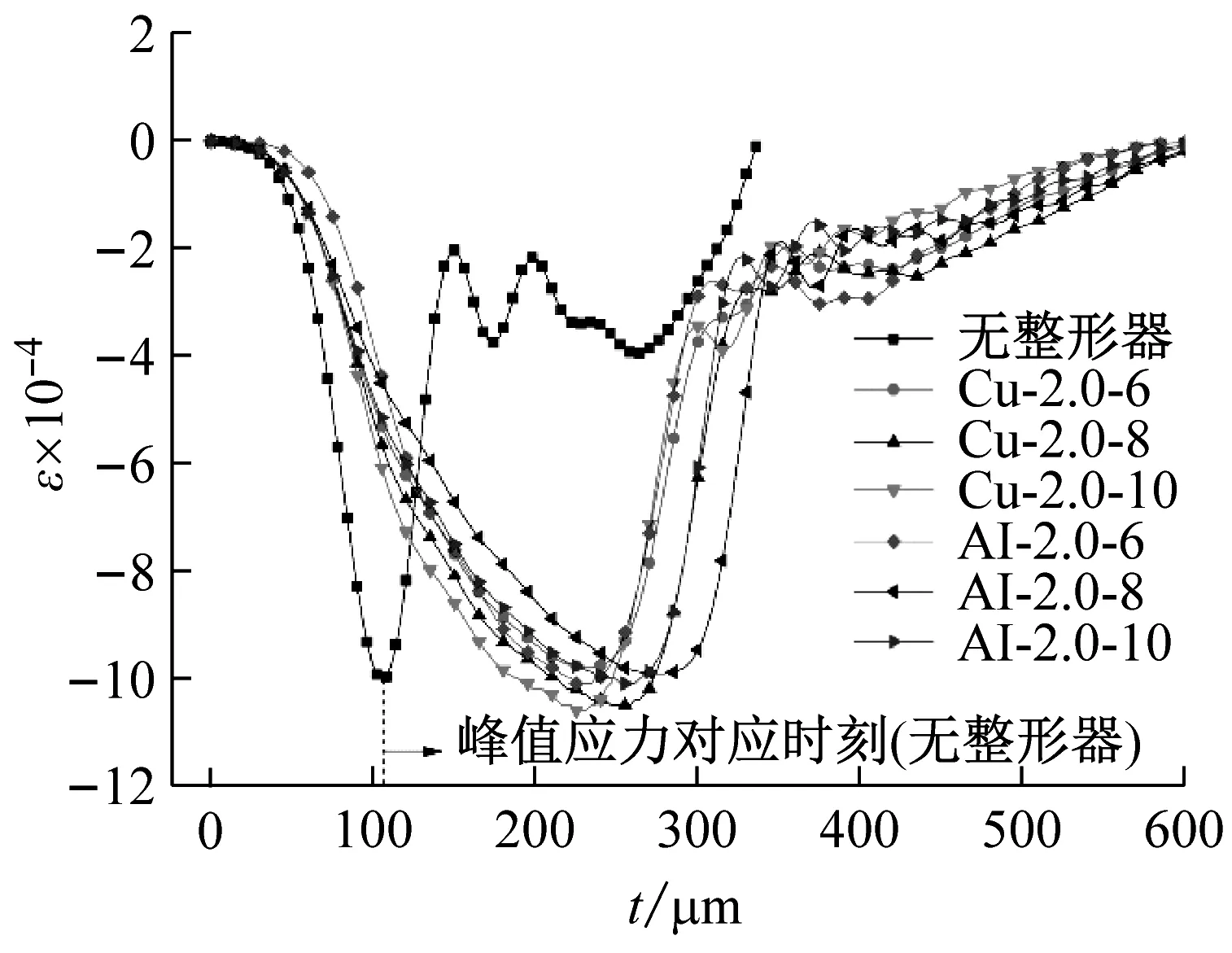
(b)透射波

(c)应力平衡因子(Cu)

(d)应力平衡因子(Al)图10 不同整形器材料下的整形效果对比Fig.10 Comparison of the shaping effect under different materials of pulse shaper
从图10(b)~(d)可以看出,未使用整形器时,试件在100 μs左右时达到透射波峰值,而在此之前应力平衡因子D处于快速下降状态,表明试件在破坏前未实现应力平衡;在使用整形器后(以直径10 mm、厚度2 mm铜质整形器和直径6 mm、厚度2 mm铝质整形器为例),试件达到透射波峰值的时间明显延迟,且在破坏(透射波峰值对应时刻)前应力平衡因子D具有明显的趋近于零的平台,表明铜质和铝质整形器均能使试件在破坏前实现应力平衡。考虑到铝质整形器相对于铜质整形器能更好的实现恒定应变率加载,因此后续的分析中选取铝质整形器进行分析。
4.2 整形器直径
为探讨整形器直径的影响,分别选取6 mm、8 mm、10 mm和12 mm直径的铝质整形器,并对其整形效果进行对比,如图11所示。分析时图11(a)中考虑整形器厚度的变化,图11(b)~(d)中整形器厚度取2 mm。
从图11(a)和(b)可以看出,直径为6 mm、8 mm和10 mm的铝质整形器在不同厚度时CSRF值均小于30%,较好的实现试验过程中的恒应变率加载。整形器直径加大到12 mm(整形器与杆件直径比为0.47)时,CSRF值相对于10 mm直径(整形器与杆件直径比为0.4)整形器出现成倍的增长,表明整形器直径增大到一定的程度后,过大的整形器截面尺寸使波形开始偏离一维应力波传播,进而难以实现恒应变率加载,图11(b)中直径12 mm整形器生成的入射波出现波形振荡也验证了这点。
从图11(c)和(d)可以看出,透射波上升沿持续时间随整形器直径的增大,呈先增大后减少的趋势(直径8 mm时最大),但在整形器直径12 mm时,透射波上升沿持续时间相对于10 mm时出现明显减少,相应的应力平衡因子D在透射波峰值之前,未出现类似于其它直径整形器趋近于零的稳定平台,表明试件破坏前并未达到应力平衡。因此,从实现恒应变率加载和试件应力平衡出发,建议整形器直径不宜大于杆件直径的0.4倍。
4.3 整形器厚度
为探讨整形器厚度的影响,分别选取1.3 mm、1.6 mm、2.0 mm、2.2 mm厚度的铝质整形器,并对其整形效果进行分析对比,如图12所示。分析时图12(a)中考虑整形器直径的变化,图12(b)~(d)中整形器直径按10 mm取值。
从图12(a)可以看出,随着整形器厚度的增加,CSRF值逐渐减少,表明增加整形器的厚度将更好的实现试验过程中的恒定应变率加载。这是由于整形器厚度增加时,入射波的上升沿持续时间和入射波的持续时间逐渐增加(见图12(b)),入射波的振荡逐步衰弱所致。
从图12(c)和(d)可以看出,不同厚度整形器下的试件破坏前应力平衡因子D均具有明显趋近于零的稳定平台,但当整形器厚度在达到2.2 mm时,相对于2.0 mm厚度,透射波上升沿持续时间出现了明显的降低。这是由于随着整形器厚度的增加,入射波强度也逐步减弱,导致加载过程中的平均应变率也随之减小。为此,整形器厚度的选择应综合考虑加载过程中CSRF值和入射波强度,对于直径10 mm整形器,相应的长径比不宜大于0.2。

(a)恒应变率因子

(b)入射波

(c)透射波

(d)应力平衡因子图11 整形器直径对整形效果对比Fig.11 Comparison of the shaping effect under different diameters of pulse shaper
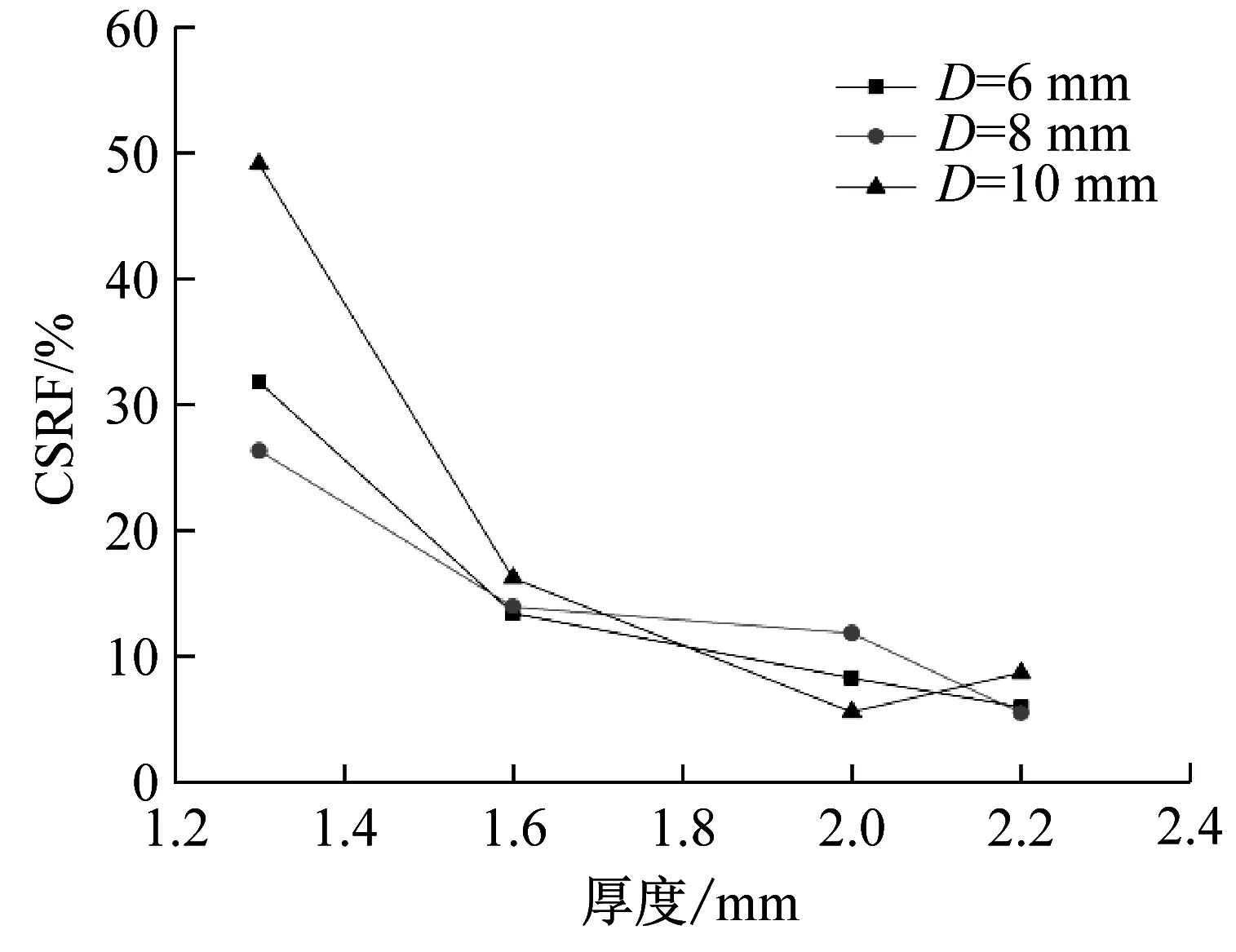
(a)恒应变率因子

(b)入射波

(c)透射波

(d)应力平衡因子图12 整形器厚度对整形效果对比Fig.12 Comparison of the shaping effect under different thickness of pulse shaper
5 结 论
本文应用LS-DYNA软件,通过优化KCC损伤模型中材料参数取值,建立了基于SHPB技术的UHPC材料冲击压缩数值模型,探讨了整形器材料、厚度和直径等参数对SHPB试验中恒应变率和试件应力平衡的影响,得到了以下结论:
(1)建立的UHPC材料冲击压缩数值模型能较好的反映整形器整形后入射波的上升平台,以及透射波取得峰值前反射波的近似水平段,具有较好的精准性。
(2)整形器是实现恒应变率加载和试件应力平衡的有效途径,相对于铜质整形器,铝质整形器能获得的更小的CSRF值,能更好的实现恒定应变率加载。
(3)整形器直径增大到一定的程度,入射波将偏离一维应力波传播,从实现恒应变率加载和试件应力平衡出发,建议整形器直径不宜大于杆件直径的0.4倍。
(4)随着整形器厚度的增加,CSRF值和入射波强度逐渐减少,从平衡加载过程中CSRF值和入射波强度出发,建议整形器长径比不宜大于0.2。

