基于量子粒子群的陀螺平衡车调节器参数优化
汪立新,单钧麟,秦伟伟,沈 强,段志强
(火箭军工程大学 控制工程系,西安 710025)
两轮前后布局的单轨式陀螺平衡车采用控制力矩陀螺作为平衡控制执行机构,具有节能环保、重量轻、行动灵活等优点,是一种适应性强、应用范围广阔的新型平衡车辆,引起了国内外公司和科研团队的广泛关注[1-2]。由于缺少车轮转动的陀螺效应及车把转向的离心力作用,陀螺平衡车的静态平衡控制实现难度较 大[3],对控制器性能要求严苛,同时它又是自主驾驶等相关应用的研究基础,因此提升陀螺平衡车静态平衡控制性能具有重要意义。
文献[4]采用极点配置方法控制平衡车静态稳定,控制器设计简洁,但对于系统极点的设计过于依赖经验,且无法对性能指标进行量化;文献[5]设计了一种滑模变结构控制器,使得稳定控制的调节时间和超调量得到改善,同时也出现了系统在平衡点附近抖动严重的问题;文献[6]阐述了基于级联扩展状态观测器的双回路自抗扰控制原理,仿真实验表明将其应用于陀螺平衡车控制能够有效提升系统稳定裕度和抗干扰能力,然而控制器复杂度和能量消耗较高,在实际应用中存在困难。
对比以上控制方法,线性二次型调节器(Linear Quadratic Regulator,LQR)作为一种多变量最优反馈控制方法,能够同时最小化系统状态量误差和控制器输出,此外还具有稳定性高、设计简单、实用性强等优点。实际应用中状态加权矩阵Q和控制加权矩阵R是设计人员要选择的主要参数,通常由专家经验和试错法相结合进行确定,需要耗费大量时间且难以保证控制效果。文献[7]采用搜索能力较强的粒子群优化(Particle Swarm Optimization,PSO)算法选取加权矩阵,设计了垂直起降微型飞行器的悬停稳定LQR 控制器,在较好满足控制需求的同时增强了系统鲁棒性,但它存在两个陷阱:易陷入局部最优和收敛速度慢。
量子粒子群优化(Quantum Particle Swarm Opti- mization,QPSO)算法是基于粒子群模型,从量子力学角度出发提出的一种新型全局优化算法。它将粒子运动状态以波函数的形式进行描述,取代传统PSO 算法中速度和位置的表示方式,使得粒子能够以一定概率出现在空间任何位置,对全局搜索性能有了很大的改进。此外,QPSO 算法模型更加简单,控制参数更少,对复杂优化问题的处理具有更好的效果[8]。
本文针对陀螺平衡车静态平衡控制问题设计LQR 控制器,使用QPSO 算法智能地搜索出使系统性能良好的最优Q、R权值矩阵参数,通过与PSO 优化和经验法得到的结果进行仿真对比和试验验证,证明QPSO 方法对陀螺平衡车LQR 参数优化的有效性。
1 陀螺平衡车系统建模
陀螺平衡车系统主要由两轮前后布局单轨式车体、控制力矩陀螺、嵌入式系统开发平台、姿态传感器、电源驱动装置,以及安全隔离架等部分组成,具体结构如图1所示。其中控制力矩陀螺是一种基于角动量交换原理实现力矩平衡控制的惯性执行机构,广泛应用于航天器姿态控制等领域[9]。
陀螺平衡车运动状态下的平衡原理同自行车较为相似,但当其处于静止状态时,车轮旋转产生的陀螺效应和车把转向引起的离心力作用等均无法产生,仅依靠控制力矩陀螺进动产生的陀螺力矩抵消重力矩分量和外界干扰力矩。其平衡控制过程为:当平衡车偏离平衡位置时,姿态传感器将敏感到的角度信号传递给嵌入式平台中的微处理器,由微处理器控制直流电机驱动控制力矩陀螺的飞轮转子在高速自转的同时和陀螺框架一起相对车体进动,根据陀螺力矩效应会对车体产生一个反作用力矩使系统回到平衡状态。

图1 陀螺平衡车结构图 Fig.1 Structure of gyroscopic balancing vehicle
由陀螺平衡车静止状态下的平衡原理,结合拉格朗日方程可以推导出其静态平衡动力学方程。将平衡车系统视为由车体、高速旋转的飞轮和陀螺框架组成的刚体系,参考坐标系建立和相关参数定义分别如图2和表1所示。
n维广义坐标下包含有势力的拉格朗日方程为


图2 模型参考坐标系 Fig.2 Reference frame of the vehicle system model

表1 陀螺平衡车参数 Tab.1 Parameters of gyroscopic balancing vehicle
式中,T为系统动能,V为系统势能,q i为第i维广义坐标,Qi为第i维广义坐标对应的广义力。
对陀螺平衡车系统有:

对广义坐标q1=θ,其广义力

联立式(1)(2)(3)(4)可得关于倾角θ的动力学方程为

式中,Ir=Irf+Irg,Ip=Ipf+Ipg。
对广义坐标q2=α,其广义力

同理,可得关于进动角α的动力学方程为

2 量子粒子群优化算法
粒子群优化算法由鸟群迁徙过程中的飞行特征抽象而来,算法中的每个粒子与生物个体相对应,由具体的位置和速度向量进行描述,通过对解空间进行搜索获得最优的适应个体和参数值,但由于每个粒子只能在确定的轨道上搜索和更新,因此无法充满全部可行域而容易陷入局部最优解。孙俊等人[10]提出用具有高度随机性的人类智能行为代替鸟群飞行运动,并通过类比将量子力学理论中的不确定性引入基本粒子群模型,建立了能够实现全局优化的量子行为模型。
假定每个粒子被束缚在以点P= (p,0)为中心的一维δ势阱中运动,并处于一定的能量状态,其量子态概率分布可由定态波函数ψ(X)进行描述:

式中,X为粒子在空间中位置,L为δ势阱特征长度。 结合蒙特卡洛法模拟出单个粒子精确位置表达式[10]

将上述结果扩展到包含M个粒子的N维搜索空间,并考虑粒子位置随时间的变化。为保证算法收敛性,对于粒子i在t时刻的第j维δ势阱特征长度Li,j(t) 需满足条件通常情况下由式(10)确定:

式中,α为收缩-扩张因子,控制粒子位置坐标的收敛性能,pbesti,j(t)为t时刻粒子i历史最优位置的第j维坐标,X i,j(t)为粒子i在t时刻的第j维坐标。则具有量子行为的一般粒子进化方程可表述为:

式中,i=1,2,…,M;j=1,2,…,N;pi,j(t)为粒子i在t时刻的第j维δ势阱中心随机坐标;gbest j(t)为t时刻M个粒子中最优位置的第j维坐标;为第j维坐标随机系数。
3 基于QPSO 的LQR 控制器参数优化
3.1 LQR 控制器设计
对陀螺平衡车静态平衡动力学方程在平衡位置附近进行线性化处理可得:

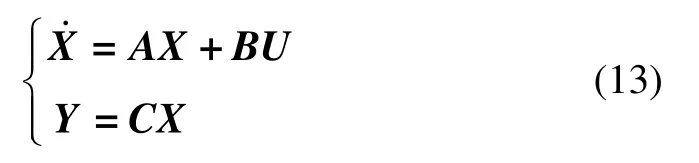
式中:

LQR 控制器设计关键是确定最优反馈控制量u(t) =-Kx(t),使得式(14)二次型指标取得最小值:
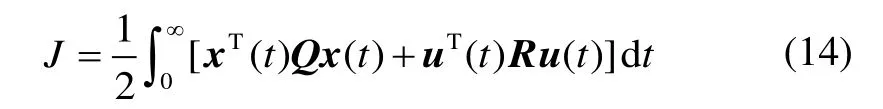
式中,K=-R-1BTP为状态反馈矩阵,Q、R为权值矩阵,矩阵P由黎卡提方程 -PA-ATP+PBR-1BTP-Q=0 确定。
可以看出:Q、R权值矩阵为待设定参数,只有适当取值才能获得较好的控制效果;传统的经验试错法耗时长且效果并不理想;随着智能算法研究的深入和完善,考虑采用量子粒子群算法进行参数优化,在Simulink 环境下搭建QPSO 优化的LQR 控制器模型,如图3所示。

图3 QPSO 优化的LQR 控制器Simulimk 模型 Fig.3 Simulimk model of LQR controller based on quantum particle swarm optimization
3.2 混合指标适应度函数
由式(11)可知,粒子每一步进化需要得到当前全体粒子最优位置和个体粒子历史最优位置坐标,因此通过建立适应度函数对粒子优劣进行评价[11],经过多次迭代提高粒子适应度函数值,最终使所有粒子收敛到全局最优位置得到相应优化参数。考虑到实际情况下系统受扰动偏离平衡位置时,应在尽量短的时间内以较小的摆动准确回复到平衡状态,把LQR 二次型性能指标、系统调节时间和响应峰值作为重要参考标准,同时为了避免框架进动饱和造成系统失稳,将最大控制量也作为一项适应度指标。由于各项指标的单位不同,绝对数值相差较大,进行对数和比值变换后定义混合指标适应度函数f为:

3.3 Q、R 矩阵优化流程
设权值矩阵Q=diag(q1,q2,q3,q4),R=r均为正定的,则待优化参数向量为x=(q1,q2,q3,q4,r)。将粒子位置坐标赋值给Q、R矩阵参数,并传递到LQR 控制器的Simulink 模型中进行系统仿真,根据仿真输出计算粒子适应度函数值,当适应度函数值收敛或迭代达到设定次数时停止更新,输出适应度函数f和Q、R矩阵参数变化曲线,QPSO 算法优化陀螺平衡车LQR 参数的具体流程如图4所示。

图4 QPSO 算法优化陀螺平衡车LQR 参数流程图 Fig.4 Flowchart of LQR parameters optimization of gyroscopic balancing vehicle by QPSO algorithm
4 仿真及试验分析
4.1 参数设置
参数设置主要由陀螺平衡车结构参数和QPSO 优化算法参数两部分组成,其中平衡车参数经对实物进行测量后计算得到:

根据以上参数求取模型状态空间方程系数矩阵:

QPSO 算法参数设置中,种群规模数为50,最大 迭代次数为100,Q矩阵参数范围为[10,500],R矩阵参数范围为[0,1],加权系数λ1= 0.05,λ2= 0.35,λ3= 0.35,λ4= 0.25,收缩-扩张因子α的一种对收敛速度提升较为有效的取值方式为[12]

式中,α1=1.78 和α2=0.5 分别是α的初始值和最终值,k是当前迭代次数,K是最大允许迭代次数。
4.2 仿真结果及分析
根据4.1 节中的参数设置进行仿真,Q、R矩阵参数和适应度函数f的寻优曲线如图5和图6所示。图5中,纵坐标q1、q2、q3、q4 为权值矩阵Q的参数值,r为权值矩阵R的参数值。从图5~6 中可以看出,算法经过30 次左右迭代后达到收敛状态,具体寻优参数值为:
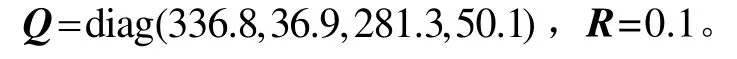

图5 Q、R 矩阵参数优化曲线 Fig.5 Optimization curves of Q and R matrix parameters

图6 适应度函数变化曲线 Fig.6 Variation curve of the fitness function
初步考察采用QPSO 进行陀螺平衡车LQR 参数优化的可行性,分别由经验法、PSO 优化和本文方法优化得到的参数在陀螺车初始倾角θ0= 0.1 rad 条件下基于Simulink 模型进行陀螺平衡车LQR 控制零输入响应仿真,结果如图7和图8所示。其中经验法选取的一组控制参数为

PSO 优化参数为

由以下条件实验得到:学习因子c1=2.5,c2=2.5,速度边界vmin= -1.0,vmax=1.0,惯性权重w=2,种群规模为50,最大迭代次数为100。
由图7和图8可以看出,3 种方法所设计的LQR控制器都能满足静态平衡控制要求,但PSO 算法和QPSO 算法优化后的控制性能明显优于经验法,同时QPSO 算法与PSO 算法相比调节时间相近,超调量更小,响应速度更快,能够满足陀螺车平衡控制的快速性和稳定性要求,同时避免因进动角超调量过大造成控制力矩陀螺自锁现象的发生。

图7 倾角θ 仿真曲线 Fig.7 Simulation curve of tilt angle θ

图8 进动角α 仿真曲线 Fig.8 Simulation curve of precession angle α
4.3 试验验证及分析
为了进一步验证QPSO 优化后的陀螺平衡车控制效果,搭建实物平台进行实时平衡控制试验。实物平台结构如图1所示,其中嵌入式系统开发平台使用NI公司的myRIO-1900,内嵌ARM Cortex-A9 微处理器和Xilinx FPGA 定制化I/O,基于Labview Real-Time/ myRIO Module 实现控制程序设计。控制力矩陀螺采用单框架构型,飞轮自转由Maxon RE35 直流电机驱动,框架进动由另一个Maxon RE40 直流电机驱动,配套的编码器可反馈进动角度信号,转速均由Copley驱动器实现精确控制,姿态传感器为Xsens Mti-300型惯性组件,用于输出平衡车倾角。myRIO-1900 可通过内置WIFI 模块与PC 端进行通信,实现控制参数调整和上位机界面实时姿态信息显示。一块12V Li电池为myRIO-1900 供电,两块24V Li 电池分别为两个Maxon 电机供电。
设置陀螺车初始倾角θ0= 0.1 rad,分别将三种方法对应的控制参数载入myRIO 1900 开发平台,试验采集从起控到平衡过程中陀螺车倾角、陀螺框架进动角和控制量信号各1000 个数据点,采样频率100 Hz,得到陀螺车倾角、框架进动角和控制量试验曲线如图9~11 所示。
可以看出,试验曲线与仿真结果基本吻合,图9中QPSO 优化下的倾角到达峰值较慢是因为实际控制中要考虑到控制量指标,而仿真时没有这一限制,试验曲线存在波动是因为实际模型中存在的未建模动态被激发所导致的。

图9 倾角θ 试验曲线 Fig.9 Experimental curve of tilt angle θ

图10 进动角α 试验曲线 Fig.10 Experimental curves of precession angle α

图11 控制量试验曲线 Fig.11 Experimental curves of controlled variable
表2为三种方法对应的具体控制性能指标值。相 较于PSO 优化和经验法,QPSO 优化下的倾角响应峰值分别降低了17.07%和38.18%,调节时间缩短了24.32%和56.64%,进动角响应峰值分别降低了16.47%和36.61%,调节时间缩短了18.03%和38.74%,最大控制量分别降低了10.78%和35.88%。

表2 陀螺平衡车控制性能指标试验值 Tab.2 Test value of gyroscopic balancing vehicle control index
5 结 论
针对陀螺平衡车线性二次型调节器Q、R矩阵参数通常依靠经验选取,需要耗费较大时间精力且无法保证得到理想控制效果的问题,本文将Q、R矩阵参数刻画为具有量子行为的粒子位置坐标,建立混合指标适应度函数评价粒子优劣,结合量子粒子群算法优化流程进行Simulink 仿真得到优化参数,并在实物平台上对优化效果加以试验验证。结果表明,量子粒子群优化参数相较于粒子群优化和经验法参数使得系统控制性能明显提升:倾角响应峰值分别降低了17.07%和38.18%,调节时间缩短了24.32%和56.64%;进动角响应峰值分别降低了16.47%和36.61%,调节时间缩短了18.03%和38.74%;最大控制量分别降低了10.78%和35.88%。

