绝对重力测量异常值的局部异常因子检测算法
吴 琼,滕云田,王晓美
(中国地震局地球物理研究所,北京 100081)
高精度绝对重力测量技术可以实现地球重力场及其随时间变化和空间分布的μGal 量级测量(1 μGal= 10-8m/s2),是重力匹配导航[1]、深空探测[2]等领域最重要、最基本的测量技术之一。虽然现阶段国内的绝对重力测量仪器还依赖进口,但随着碘稳频激光器研制、高精度时频测量、真空技术以及精密机械加工等领域的不断进步,自主研发的高精度绝对重力仪正逐渐成熟并向实际应用领域拓展[3]。
绝对重力仪一般采用分组多次测量求平均的方式获得最终测量结果。在实际测量过程中,仪器自身的系统振动和测点的背景振动对测量结果的影响比较明显,是引起测量结果离散度变大和导致测量结果中出现异常点的主要原因[4]。对单次测量的时间-位移坐标进行最小二乘拟合时,由于测量误差的存在,同样会导致测量结果出现异常点[5]。此外,激光器和铷原子频标的电子系统长期连续工作时可能存在的瞬时扰动,使得提供的长度基准和时间基准会发生小概率的跳变,从而造成单个测量结果异常甚至突变。
目前针对测量过程中的异常点(离群程度较小)和突变点(离群程度较大),一般采用的处理方式是在组测量结果计算时,采用基于正态分布的一元异常点检测算法进行异常点的检测和舍弃。但实际测量结果表明,在单组100 次下落的绝对重力测量过程中,如果异常点出现的个数较多(大于5 个)或离群程度不一样的时候,该算法会造成某些异常点的漏检,降低组测量结果的测量精度并可能在最终测量结果中引入测量偏差。
随着人工智能(AI)技术的不断进步,异常点检测作为一个特定的研究方向,在过程工业、金融业、通信领域得到普遍关注和广泛应用[6]。异常点检测算法一般基于某个存在的模型,定义一个区间,处于区间外的点被定义为异常点。根据模型的定义可以将异常值检测算法分为基于概率分布模型[7]、基于距离和聚类[8]、基于数据分类[9]等。
考虑到在自主研发的绝对重力仪测量过程中,单组测量数据一般会被预先设定为50 或100 个,但要求快速在线完成异常值检测,故本文利用基于欧式距离的局部异常因子LOF 算法(Local Outlier Factor)[10]对组内测量数据进行异常值检测。通过对LOF 算法关键唯一参数——“邻域宽度”的选取及模拟仿真,并与传统的基于正态分布的一元异常点检测算法进行对比确定,基于LOF 算法的异常值检测可以实现对组内测量异常点在线、快速、精准检测,同时还可以消除漏检和误检现象,从而提高自主研发绝对重力仪测量的精度和准确度。
1 算法原理
1.1 一元正态分布异常值检测算法存在的问题
目前绝对重力测量中,针对测量过程中出现的异常值一般采用一元正态分布异常值检测算法进行判断和排除,基本算法原理如下:
对于一次测量获得的n个测量结果中,定义第i个测量结果xi的异常值Zi为:
其中,为本组测量结果的平均值,σ为本组测量的标准差。
如果Zi≥ 3,则认为该值为异常值,在本次测量结果中应予以舍弃。但是在自主研发的绝对重力仪测量过程中,这种检测算法很容易造成异常值的漏检。为了说明这一现象,首先构建一组测试用的数据集,包含异常点和突变点,具体如下:
1)构建数据集,包含100 个数据,分布区间为400~600,单位为μGal,服从标准正态分布;
2)在第10、30、49、51、90 位置的测量结果上分别叠加600、-600、-400、-400、400,构建异常点;
3)在50 和70 次测量结果上叠加-2500 和1500,构建突变点。
如图1所示,当不考虑50、70 位置的突变点,对构建的数据集使用一元异常值检测算法时,设置的异常点被正常检出。但是当数据集的第50 和70 位置被设置为突变点后,第10、30、49、51、90 位置的异常点均被认为是正常值保留。可以说当测量的数据中出现突变点时,离群程度较小的异常点被漏检并参与最终测量结果的计算。
这种现象出现在项目组自主研发绝对重力的测量 结果中,直接影响了最终测量结果的准确度和精度。故需要引入新的异常值检测算法,不仅可以完成对离群程度较大的突变点进行检测,同时还要避免对离群程度较小、连续出现的异常点的漏检。本文选用计算速度快,检测效果好的局部异常因子LOF 算法。
1.2 局部异常因子LOF 算法基本原理
局部异常因子LOF 算法的计算流程如下:
Step 1:定义测试数据集内的 p(x1,y1)点和 q(x2,y2)点之间的距离:

Step 2:定义点p 的邻域 D { p} 宽度k:
对于点o ∈ D:
1)至少有k个点 o' ∈ D { p},满足:

2)至多有k-1 个点 o' ∈ D { p},满足:
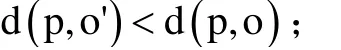
Step 3:计算点p 的可达距离:

Step 4:计算点p 局部可达密度:

Step 5:计算点p 的局部可达因子LOF:

从LOF 的定义可以看出,在点p 的邻域内,其他点的局部可达密度大,而点p 的局部可达密度小,则点p的局部异常因子就大,即点p是一个局部异常值。
Breunig 等[10]还证明了在测量结果组成的数据集 合中,正常值的LOF 一般在1 左右并小于2,因此可 以将LOF 值大于2 的作为异常值或突变值。
1.3 LOF 算法参数邻域宽度k 选取
从1.2 节LOF 的定义可以看出,对测量数据的每个测点计算其LOF 时,只有1 个参数,即邻域宽度k影响最终检测结果。因此本部分通过数值模拟确定k在利用LOF 算法完成绝对重力测量数据检测时的取值。
为了更好地测试k对最终检测结果的影响程度,基于1.1 节构建的测试数据,主要针对以下几方面进行LOF 算法的检测效果测试:
1)存在突跳点的情况下离群程度较小的异常点检测;
2)存在连续异常、突跳情况的异常点检测;
3)原始数据标准差较大情况下异常点检测。
不同k值对应的各个测点的LOF 计算结果如图2所示。LOF 的大小以不同的颜色标识,可以看出随着邻域宽度k取值从0 到100 的变化,LOF 算法的检测效果的变化:
k=1~4:漏检率和误检率较高;
k=5~20:对1)、2)、3)项内容均可以正确检测,各个异常点的LOF 值明显可辨(均大于20);
k=21~100:出现不同程度的漏检现象。
图3显示了不同的参数k对应的异常点检测效果。其中第1 和第2 条曲线分别显示了将检测出的异常点删除后得到的新数据集的均值和标准差,第3 条曲线显示的是检出的异常点个数。
测试数据集共设置7 个异常点,从图2和图3的第3 条曲线可以明显看出,在5≤k≤60 的区间范围内,7 个异常点可被准确检出,包含第49、50 和51三个连续异常和突变点,异常点检出后的均值和方差 与模拟数据预设的均值和方差相比均小于5 μGal。

图2 不同k 值对应的各个测点的LOF Fig.2 Local outlier factor of each measurement point corresponding to different k values

图3 不同k 值时异常点检测效果 Fig.3 Effect of outlier detection under different k values
在实际的绝对重力测试过程中,每组测量次数一般设置为50~100,24 h 完成48 组测量。
综合图2、图3,考虑运算的速度、异常点LOF 值的可辨识性和算法检测的准确性,邻域宽度k的取值设定为10,并要求测量时每组测量次数不少于20 次。
2 实测数据的LOF 与一元正态分布异常值检测算法结果对比
自主研发的激光干涉绝对重力仪于2018年2月9日至4月1日,在中国计量科学研究院昌平园区2017国际绝对重力比对基地的8 号测点进行连续观测。测试期间设置每组测量50 次,组间时间间隔是4 h,共完成14 650 次测量。测量结果的准确度和测量精度依据《中国大陆构造环境检测网络技术规程—绝对重力测量部分》之“成果计算”部分完成计算。
图4所示为连续2 组,共100 个原始测量结果、一元异常值检测结果和本文讨论的LOF 算法完成的异常点检测结果(k=10,LOF 大于2 认为是异常值[10])。
从图4可以看出,LOF 算法将负向离群程度较大的第27 点作为异常值准确检出,但是一元异常值检测算法则将其作为有效值保留,这样在计算这100 个测量结果的平均值时,基于一元异常值检测算法的结果肯定小于基于LOF 算法检测的结果,影响了测量结果的准确度。

图4 实测数据的异常值检测算法对比 Fig.4 Comparison on outlier detection algorithms based on measured data
图5是分别利用一元异常值检测算法和LOF 算法,按照50 个测量结果为一组计算绝对重力组测量结果的误差棒图对比。考虑到在测量过程中,2018年2月 12日河北廊坊永清县Ms4.3 地震对仪器参考棱镜的影响造成的测量结果异常,图5中显示的是本次连续测量期间震后2018年2月22日至4月13日共计50 天的连续测量数据。可以看到,LOF 算法完备地完成测量结果中异常值的检测,组测量结果的误差棒图没有出现异常结果,200 组的测量结果为980XXX783.0 μGal(仪器测量高度位置),测量精度为1.94 μGal。
基于一元异常值检测的组测量结果中,第138 组 和152 组出现异常结果,表明这两组内有较为明显的离群点未被正确检出,且参与了组结果的计算,200组的测量结果为980XXX782.39 μGal(仪器测量高度位置),测量精度仅为427.15 μGal,远大于利用LOF算法进行异常值检测后的计算结果。
图6为200 组测量结果,利用一元异常值检测算法和LOF 算法进行异常值检测后单组测量精度,第138 组和152 组内由于存在未被检出的异常点,造成 单组测量精度偏差。而对其他的单组测量精度对比,基于LOF 算法的组测量结果精度与一元异常值检测算法的结果相比,平均小9.37 μGal。

图5 两种异常值检测算法完成异常值检测后组测量结果的误差棒图对比 Fig.5 Comparison on error bars of the two outlier detection algorithms

图6 两种异常值检测算法完成异常值检测后单组测量精度对比 Fig.6 Comparison on precisions of the two outlier detection algorithms
3 结 论
本文首先描述了目前自主研发绝对重力仪中普遍使用的基于正态分布的一元异常值检测算法的漏检现 象。然后引入LOF 算法,通过对同一组测试数据集进行计算的结果表明,LOF 算法规避了存在离群程度不同的异常点时的漏检现象,同时对连续出现的异常点和突跳点均可以准确检出。该算法非常适合自主研发绝对重力仪组测量结果的异常值检测。
从LOF 算法的定义可以看出,影响该算法计算结果的唯一参数是邻域宽度k。对此利用构建的数据样本进行数值模拟计算的结果表明,对于100 个数据样本组成的数据集,5≤k≤60 的区间范围内可以检出离群程度不同的全部异常点,无漏检现象。考虑实际测量中单组测量次数一般为50~100 次,从计算时间和异常值检测效果的综合考虑,取k=10。
最后利用LOF 算法,取邻域宽度k=10,对自主研发绝对重力仪长期连续观测数据进行处理,对比了一元异常值检测算法和LOF 算法的检验效果。结果表明,利用LOF 算法可以在线、快速、精准地完成异常值检测,明显提高总体计算结果的精度,同时不会影响测量结果的准确度。在下一步工作中考虑将LOF 算法代替一元异常值检测,作为自主研发绝对重力仪单组异常值检测的通用算法。

