供求曲线移动的数学原理

甘肃 苟 强

供求曲线是必修一《经济生活》中的一个教学难点，也是高考的一个热点。近些年来，广大教学界同仁对此进行了诸多探讨，探讨的过程也是争论的过程，遗憾的是，这些探讨和争论并未取得多少共识。

供求曲线理论是西方经济学的基础理论，供给曲线和需求曲线是经过严格的数学证明、推导而来的，不是凭空想象画出来的。西方经济学的微观经济学部分有一半的内容就在证明和推导这两条曲线，当然，这远远超越了高中学生的数学基础，也超出了我们高中教学的范畴。本文以高中数学为基础，对供求曲线的移动做一简化分析和通俗性解读，主要为学生提供一个可理解的结论性认识。大学西方经济学的教学是按照初级课程、中级课程和高级课程三个层次，经过本科低年级、本科高年级和研究生三个阶段渐次展开的，三级课程的区别主要在于所运用数学知识的深度和难度不一样。本文是基于高中数学的分析，可称之为供求曲线的预备级课程。

一、供求曲线

市场对某种商品的需求取决于多种因素的影响，主要为该商品的价格、消费者的收入水平、相关商品（替代品和互补品）的价格、消费者的偏好和消费者对该商品的价格预期等。也就是说，市场对某种商品的需求不仅取决于商品的价格，还受到其他众多因素的影响，用数学语言表示就是，商品的需求不是一个一元函数，而是一个多元函数，即Q=f（P，Y，PR，Pre，Ex），Q表示需求，P表示该商品的价格，Y表示消费者的收入水平，PR表示相关商品的价格，Pre表示消费者的偏好，Ex表示消费者对该商品的价格预期。但在西方经济学中，需求函数特指商品的需求与商品的价格之间的函数关系，换句话说，需求是关于价格的一元函数，并非关于众多因素的多元函数，即Q=f（P），其中Q是因变量，表示需求；P是自变量，表示价格。这样处理的潜在假设是，其他条件不变，即消费者的收入水平、相关商品的价格、消费者的偏好和消费者对该商品的价格预期等因素均保持不变。

需求曲线是需求函数的几何表示，是根据需求函数将需求与价格之间的各种对应组合在平面直角坐标系中绘制而成的一条曲线。在这里，需要特别明确两个概念：需求量的变动和需求的变动。

需求量的变动。需求量的变动特指在其他条件不变的情况下，由价格变化所引起的需求的变化，其实质是在需求函数中，自变量价格P变化后，因变量Q如何变化？表示在图形上，就是需求曲线上点的移动。例如，在图1中，P1减少为P2后，Q1增大为Q2，即A点向B点的移动。

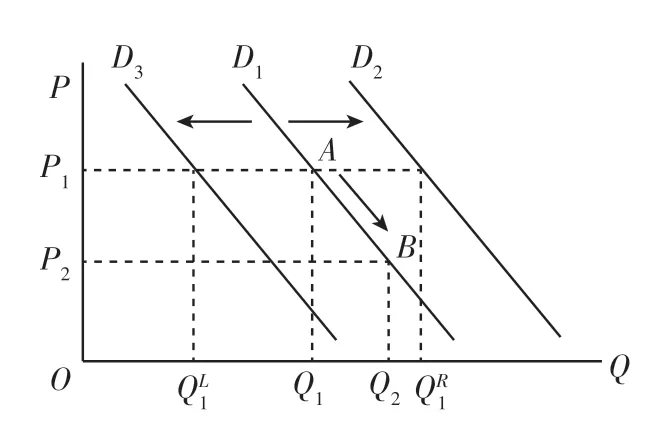
图1

需求的变动。需求的变动特指在价格不变的情况下，由其他因素变化所引起的需求的变化，表示在图形上，就是需求曲线的移动。例如，在图1中，需求曲线由D1右移至D2，表示由于其他因素变化，引起需求增加，因为在价格保持P1（P1为任意点）不变的情况下，D2上与P1相对应的点大于D1上与P1相对应的点Q1。需求曲线由D1左移至D3，表示由于其他因素变化所引起的需求的减少，因为在价格保持P1（P1为任意点）不变的情况下，D3上与P1相对应的点小于D1上与P1相对应的点Q1。

供给曲线与需求曲线大体类似，在此仅作简要介绍。

影响市场对某商品供给的因素主要为该商品的价格、生产的成本、生产的技术水平、相关商品的价格和生产者对该商品的价格预期。某种商品的市场供给是所有这些影响因素的函数，即供给函数实际上也是一个多元函数。但如果假定其他条件不变，仅考虑价格变化对其供给的影响，即把某种商品的供给仅看作是该商品价格的函数，则此时供给就是关于价格的一元函数。如同需求曲线一样，供给曲线是供给函数的几何图示，是根据供给函数把供给与价格之间的各种对应组合在平面直角坐标系中连接而成的一条光滑曲线。无论是需求曲线，还是供给曲线，既可以是直线状，也可以是曲线状，但为了降低难度和分析问题方便，在高中阶段的教学中，我们一般都选取直线状。需求函数是对商品价格变动和商品需求变动之间规律的数学化表达，同理，供给函数反映的是商品价格变动与商品供给变动之间的规律。需求函数和供给函数是把这些规律抽象化成数学形式，而需求曲线和供给曲线则是把这些规律图示化、可视化。与需求曲线一样，此时，仍有两个需要特别加以区分的概念：供给量的变动和供给的变动。简言之，供给量的变动表现为点的移动，供给的变动表现为线的移动。进一步说，供给量的变动是指在其他条件不变的情况下，由商品价格变动所引起的商品供给的变动。在几何图示中表现为供给曲线上的某一点沿着供给曲线运动到另一点。供给的变动则指在商品价格不变的条件下，由其他因素变动所引起的商品供给的变动，在几何图示中表现为供给曲线本身发生位移。

二、数学解读

需求曲线的难点主要在于：需求量的变动和需求的变动，解决这一难题的关键是函数的几何图示。在理论上，多元函数的自变量可以有无数个，即y=f（x1，x2…xn），但当函数的自变量超过两个时，就没有办法进行几何图示。因为函数是一元函数时，即y=f（x）时，我们可以在平面直角坐标系中对其进行几何图示；函数为二元函数时，即z=f（x，y）时，我们可以在空间直角坐标系中对其进行几何图示；函数为三元函数时，即y=f（x1，x2，x3）时，我们就无法对其进行几何图示。

对于一元函数y=f（x），如果我们要研究自变量x的变化对因变量的影响，一般是求其导数。导数大于0，则y与x同向变化，即y随x的增大而增大，随x的减小而减小；导数小于0，则y与x反向变化，即y随x的增大而减小，随x的减小而增大。对于多元函数y=f（x1，x2…xn），如果我们研究其中某个自变量xi（i=1，2…n）的变化对因变量y的影响，应该怎么办？其实，方法和一元函数是一样的，即将除xi之外的其他自变量视为常量，然后求y对xi的导数，专业术语称之为“偏导数”。在经济学的研究中，我们经常会见到诸如“在其他条件不变的情况下”这样的说法。所谓“其他条件不变”，其数学含义如下：对于多元函数y=f（x1，x2…xn），如果要求y对xi（i=1，2…n）的偏导数，除xi（i=1，2…n）之外的所有其他自变量即是“其他条件”，其他条件不变就是除xi（i=1，2…n）之外的所有其他自变量视为常数。

现实中，在研究因果关系时，我们会常碰到两种类型的因果关系，即一因一果和多因一果。一因一果对应的就是数学上的一元函数，多因一果对应多元函数，多因一果更为多见。对于多因一果事件，多因联动影响结果的情况更为常见，如果多因联动，结果又会如何呢？把这个问题转换成数学语言就是，仍然以二元函数z=f（x，y）为例，x、y同时变动，z如何变动？这个问题在数学上也有办法，即求全微分。当然，这远超出了初等数学和高中教学的范畴，本文只是略微提及，不做探讨。对于多因一果事件，高中阶段的教学和考试，还是以他因未变，一因变动对结果的影响为主。

下面以一个有具体函数解析式的二元函数为例来说明。假设z=f（x，y）=x+y2（y＞0），求z对x的偏导数时，视y为某常数b，则z=f（x，y）=x+y2=x+b=f（x），即二元函数实际上就转化为一元函数，转化后的一元函数就可以在平面直角坐标系上进行图示。如图2所示：

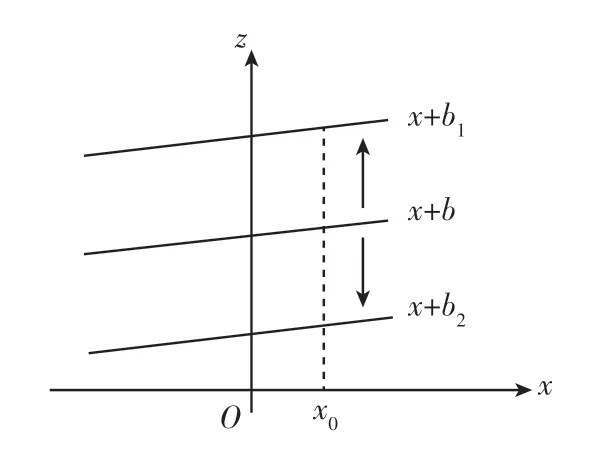
图2

那么，在这个平面函数图像中，没有自变量y对应的轴，如何看出自变量y变化对因变量z的影响呢？具体做法是，根据函数解析式z=x+y2，求z对y的偏导数=2y，由于y＞0，所以，=2y＞0，故当x保持不变，y变动时，z与y同向变动，即y增大时，z也随之增大，在函数图像上就表现为曲线上移。例如，当x保持x=x0不变时，y由b增加为b1时，函数就由x+b上移至x+b1，y由b减少为b2时，函数就由x+b下移至x+b2。这种方法的优点是，把三维空间上的函数图像转化为二维空间上的函数图像，更加直观，可视化效果更好。y=x+b这个函数随参数b的变化上下移动，在初中数学中就学习过，所以在教学中选用y=x+b作为范例，学生较为熟悉，教学效果较好。

需求函数Q=f（P）的移动常表现为左移和右移，因为在需求函数的图示中，习惯把自变量P放在纵轴上，因变量Q放在横轴上。此种表示方法虽有悖于数学常规，但也只是经济学的传统，并无其他特殊含义。

三、解题策略

在有关供求曲线移动的高考试题中，线的移动是考查的重点。我们学过的需求函数Q=f（P）是需求对价格的一元函数，但考题往往会给定一个除价格之外的自变量，要求考生分析该变量变化对需求的影响并图示出来。这其实就是本文第二部分所讨论的求偏导和函数图像平面转换问题。由于题目一般不会给出函数的具体解析式，故无法求偏导，我们会选择一个替代性的办法代替求偏导，即通过题中给定的信息运用专业知识判断该变量对需求的影响。

仍以实例来说明。例如，某商品的需求函数Q=f（P），该商品的替代品价格Palter下降时，该商品的需求如何变动？需求曲线如何移动？在此例中，影响该商品需求的因素实际上有两个，即其自身的价格P和其替代品的价格Palter，故原需求函数可拓展为升级版的需求函数Q=f（P，Palter），即Q是关于P和Palter的二元函数。此时，当Palter变化时，求Q的变化并不用求偏导数，而是根据专业知识即可判断。由于Q和Palter同向变动，Palter增大时，Q增大，Palter减小时，Q减小。对应在函数图像上，就是P保持P0（P0为需求曲线上的任意点）不变，Palter增大时，函数图像右移，Palter减小时，函数图像左移。在探讨Palter变化对Q的影响时，务必保持P不变。如图3所示：

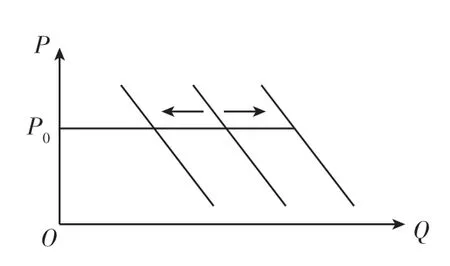
图3

马克思认为：“一种科学只有在成功地运用数学时，才算达到了真正完善的地步。”科学精神是思想政治学科的四大核心素养之一，是基础性素养，也是达成其他素养的基本条件。因此，无论是从教学的角度讲，还是从培养学生科学精神的要求来看，对数学的刻意回避无疑是有害的。在对供求曲线既往的探讨和争论中，大家的功夫主要花在了曲线上，但对曲线背后的函数并没有作深入探讨，要知道供求曲线只是供求函数的图形化，图形是由函数决定的，没有函数，何来图形？这种浮于表面而不求根本的做法，其根源在于思政课教师对数学的天然抵触，遇着数学绕道走。比数学之难更可怕的是这种对数学不友好的情感。毕竟，高中教学是以高中学生所学习的初等数学为基础的，而我们绝大多数人都是经历过高考的人，有些甚至还学习过高等数学。所以，问题不在于数学知识不够，即使数学知识欠缺，也可以再学，或者跨学科协同，向数学教师求助，关键是我们要克服对数学的恐惧。如果这种对数学持有偏见的传统得不到改良，很多科学很有可能会在我们的思政课堂上异化为伪科学，学生科学素养的培养也将沦为空洞的口号。进入核心素养的新时代，作为思政课教师，学习数学、应用数学是专业发展的重要内容。