微积分传入前后清朝数学家对微积分相关问题的研究

李丹 大连财经学院

微积分传入我国是以1859 年李善兰与伟烈亚力合作翻译出版《代微积拾级》为标志的。微积分传入前后这段时间，项名达和夏鸾翔等数学家分别将开方术应用于无理式积分的相关问题，如椭圆求积术等问题的研究，亦有较为突出的成就。而这些成就恰巧在微积分传入前后这段时间所取得，具有较为重要的意义。

项名达（公元1789—1850），原名万准，字步莱，号梅侣，浙江仁和人。嘉庆二十一年（1816）举人，考授国子监学正。道光六年（1826）进士，改官知县，呈请归学正本班铨补。未几乞假归，主讲杭州紫阳书院，直至1846 年辞去讲席，专事著述。著有《下学庵算学》三种各一卷，分别为《勾股六术》（1825）、《三事和较术》（1843）、《开诸乘方捷术》（约1845），还有未完稿《象数一原》六卷（1849）。戴煦（公元1805—1860），字鄂士，号鹤墅，又号仲乙，浙江钱塘人。十五岁，入杭州府学，后绝意进取。戴煦读书兴趣广泛，数学、音律、文学、古文字、绘画、篆刻乃至堪舆无不精究，而以数学为主要研究领域。1860 年3月19 日，太平天国军攻克杭州，戴煦随兄自尽。戴煦著有《四元玉鉴细草》三卷、《求表捷术》四种共九卷。

项名达和戴煦二人关系密切。1826 年，戴煦初成《四元玉鉴细草》若干卷，项名达阅后即与戴煦相见，二人遂为忘年之交。二人均治学严谨，学术交往频繁，许多成果两人都相互讨论研究。戴煦遵项名达遗嘱为其校补《象数一原》并补第七卷。二人在开方术的研究上亦交流频繁，故本章讨论二人的研究。

项名达有未完稿的《象数一原》六卷（1849），戴煦受项名达嘱托于咸丰七年（1857）校补并补卷七椭圆求周术图解。该著作在三角函数幂级数展开式和椭圆求周方面均有深入的研究。其中，卷六是在董 诚研究的基础上，对椭圆求周术的研究，卷七是戴氏所补图解。以 a，b 分别为椭圆的长半轴和短半轴，以p 为椭圆周长，e 为离心率，则项名达所给出的椭圆周长公式为

戴煦指出项名达的椭圆求积术以大辅圆立算，故以“借大积”开平方，也可以小辅圆立算，以“借小积开平方。”于是，戴煦借助《开诸乘方捷术》中的补第一术，亦即《续对数简法》中的“以本数为积求折小各率第二术”，

给出了椭圆周长的另一个公式

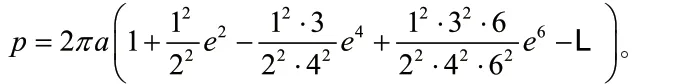
项名达和戴煦所给出的椭圆周长公式是正确的，他们运用了椭圆基本定理，开方术及相似等知识。他们的工作是在微积分传入之前，而其思想与椭圆积分的原理相同。他们的方法在微积分传入前，对解决微积分所研究的相关问题具有重要的意义，而微积分传入后，对我国数学家理解微积分知识也有一定的作用。但是，他们的方法较为初等，因此计算量很大。

项名达和戴煦之后，夏鸾翔也研究了曲线求积问题，得到了一般的椭圆弧长公式。

夏鸾翔（公元1825—1864），字紫笙，浙江钱塘人。“夏姓是杭州一带的大族，历史上出过不少达官名儒，……清初以后夏族渐衰，然家世好学，门风濡染，知名于乡里者仍不少。”夏鸾翔自小刻苦勤学，尤其酷爱绘画和诗歌。同样是因为受到家庭影响，夏鸾翔醉心于功名，多次参加科举考试，但均为中第。

1845 年，夏鸾翔因为阅读戴煦的著作，遂登门拜访而结识同乡戴煦，后又与项名达相识，拜项名达为师，从此系统地学习数学和天文学知识。1857 年，夏鸾翔通过输饷议叙的方式得到了一个詹事府主簿的职位，1858 年，因丧母而归家守孝，这个时期，夏鸾翔与时任江苏巡抚的数学家徐有壬有所交往，在学术上也有所交流。1860 年初，李善兰应徐有壬之邀来到苏州做幕宾，夏鸾翔很可能结识了李善兰，并见到了李善兰与伟烈亚力合译的《代微积拾级》，从而因此学习到了微积分的知识。后来，因为太平天国运动，苏杭一带战事不断，夏鸾翔为逃避战乱，于1863 年到达广州，同时带去了自己的主要著作和戴煦的《对数简法》。不久之后，夏鸾翔便结识了邹伯奇和吴嘉善等人，这些数学家互相探讨交流，得到了一些数学研究成果。1863 年底，广东巡抚郭嵩焘开始筹建舆图馆和同文馆。筹建中的同文馆拟设西文教习、中文教习各一人。郭打算聘请夏鸾翔为中文教习，可惜，夏鸾翔未到任便于1864 年因病去世，享年仅42 岁。

夏鸾翔的主要数学著作有《少广缒凿》一卷）（约1850）、《洞方术图解》二卷（1857）、《致曲术》和《致曲图解》各一卷（约1860—1861）和《万象一原》九卷（1862）等。夏鸾翔去世后，邹伯奇等甚为痛惜，邹嘱托吴嘉善搜寻夏鸾翔的著作，后来郭嵩焘亦出资。直到1874 年，邹伯奇的后人在出版《邹征君遗书》时，才将夏氏的部分著作（以上所列前四种）一并刊印。

他的相关研究成果主要记载在《致曲术》《致曲图解》以及《万象一原》中。夏鸾翔在《致曲术》“椭正弦求椭弧背术”中给出了椭圆弧长的幂级数展开式。对于椭圆，设L 为椭圆上从点到点的一段椭弧长，则

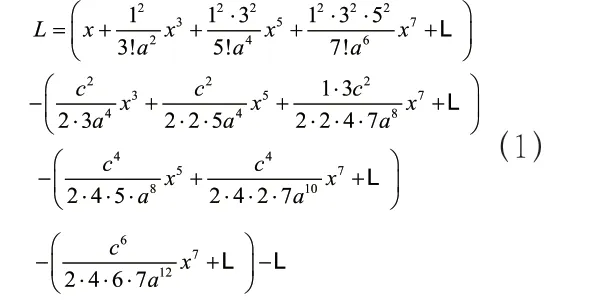
夏鸾翔在《致曲术》中并没有给出详细的推导过程，可以根据夏氏相关著作对该式予以说明，如下

李善兰和伟烈亚力翻译出版的《代微积拾级》的卷十四第八款给出曲线的弧长微分式为

卷十八还给出椭圆弧长公式

在上式中的

将上列各式代入式（2）可得式（1）。而式（1）是表示椭圆从点到点的弧长，若将点换为，即在式（1）中令，再乘以4，整理可得项名达所给出的椭圆周长公式。

夏鸾翔利用开方术等知识得到了椭圆弧长的一般公式，其成果比项名达的更具一般性。夏氏的成果在微积分传入我国之后，并且从他的著作中可以得知其已经接触学习到了《代微积拾级》中的相关知识。然而，在处理被积函数中的无理式的展开式时，他抛开了《代微积拾级》中的泰勒公式和马克劳林公式，而应用了中国传统的递加数的知识对二项式函数进行展开，然后再逐项求积分。在当时的许多中国数学家看来，“‘微分术’几乎等同于级数展开式的求法，而级数展开法在中国传统数学中‘递加数’就可以解决，因此在夏氏看来，微分术就是‘递加数’”。

综上，在微积分传入以前，中国数学家借助开方术的研究成果，解决了一部分曲线求积问题，他们因此易于接受积分中无限分割的思想。但是，由于开方术的知识背景是以递加数为基础，这使得中国数学家在学习微积分的时候认识过于狭隘，往往认为与中国的递加数没有区别，而阻碍了广大数学家对微积分的吸收与研究。