基于预测碰撞点带落角约束的导引律设计
史绍琨,赵久奋,尤 浩
(火箭军工程大学,西安 710025)
0 引言
为了增强导弹的毁伤能力,需要考虑复杂地形条件下目标的运动倾角,控制导弹以指定的角度攻击目标[1]。偏置比例导引律可以实现对落角进行控制,具有结构简单、推导方便、易于控制的优点[2]。关于实现落角约束的偏置比例导引律最早的研究,是Lee 等[3]在假设偏置项为常数的条件下,推导了带落角约束的偏置比例导引律。此后,不断有研究对偏置比例导引律进行变形推导,但大多是针对地面固定目标实现带落角约束的制导控制,针对带倾角运动目标实现落角控制的偏置比例导引律鲜有报道。因此,本文针对坦克、地面装甲车等运动目标,设计了攻击运动目标的偏置比例导引律。此外,制导律中涉及的一个重要参数是剩余飞行时间(tgo)[4]。剩余飞行时间(tgo)估计的准确与否,直接关系到脱靶量、过载等重要制导性能。因此,设计精准的剩余飞行时间估计方法也是本文研究的重要问题。
文献[5]推导了针对地面固定目标带落角约束的偏置比例导引律,并在考虑弹道曲率的情况下对剩余飞行时间进行了较为精确的估算。文献[6]在线性RPN/PN 制导律条件下,针对顺轨和逆轨飞行轨迹的特点,基于预测碰撞点对剩余飞行时间进行估计。文献[7]将剩余飞行时间的计算转化为求解导弹前置角γ 变化到0 的时间,对剩余飞行时间进行估算;文献[8]在未考虑目标运动倾角的情况下,设计了带落角约束的偏置比例导引律,并与其他导引律进行了仿真比较。
本文在文献[5-8]的基础上推导了攻击运动目标带落角约束的偏置比例导引律,并对导引律中出现的重要参数剩余飞行时间tgo进行基于预测碰撞点的剩余飞行时间估计。最后将设计的剩余飞行时间估计方法代入推导得到的导引律,并分析了导引律的性能。
1 攻击运动目标带落角约束的偏置比例导引律设计
考虑二维平面内导弹攻击运动目标情况,弹目相对运动关系[9]如图1 所示。
图1 中OXY 是地面惯性坐标系,M、T、P 分别表示导弹、目标和弹目碰撞点。an为导弹法向加速度,R 表示弹目视线。q 为弹目视线角,规定由弹目视线R 逆时针旋转到水平基准线时为正;θm和σm表示导弹的前置角和弹道倾角,规定导弹速度vm顺时针转向弹目视线R 时前置角θm为正,规定导弹速度vm位于水平基准线下方时弹道倾角σm为正。θt和σt表示目标的前置角和弹道倾角,θt和σt的正负定义同θm和σm相同。vm和vt表示导弹和目标的速度,假设都为常值。则弹目相对运动方程[10-11]为:
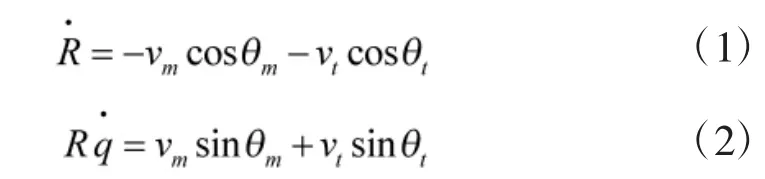
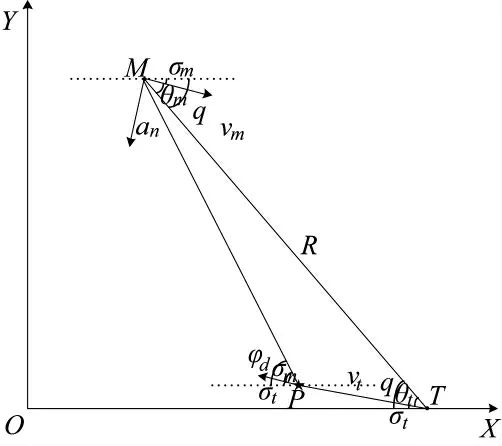
图1 弹目相对运动关系示意图
导弹的运动方程为
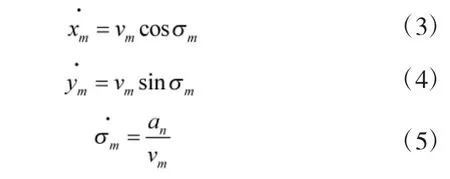
目标的运动方程为

联系方程为

制导方程为

式中:N 为比例系数,aB为偏置项,通过在传统比例导引的基础上增加一项偏置项来实现对落角的控制。
进行带落角约束偏置比例导引律设计的核心是制导方程的求解,制导方程求解的关键是偏置项aB的解算,下面将进行偏置项aB的推导。
将式(10)代入式(5),得到

根据导数的定义,在某一小段时间Δt 内,有
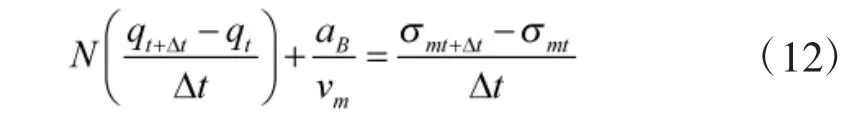
式中,下标t 和t+Δt 分别表示Δt 时间段的初始时刻和末时刻,假设aB在每个Δt 时间段内均为常数,则将式(12)中的Δt 扩展到整个飞行时间tf,并在方程两边同时乘以tf得
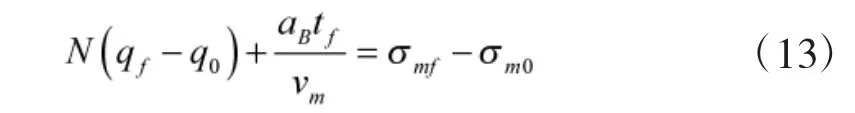
式中,下标0 和f 分别表示飞行过程的初始时刻和末时刻。将式(13)整理变形,并将总飞行时间tf用当前时刻剩余飞行时间tgo表示,初始时刻t0用当前时刻t 表示,得到aB的表示式为

设导弹攻击目标的期望攻击角为φd,则根据图1 中的几何关系,有

根据弹目相对运动方程式(2),当导弹击中目标R(tf)=0 时,有
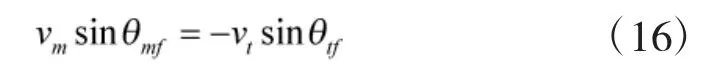
即
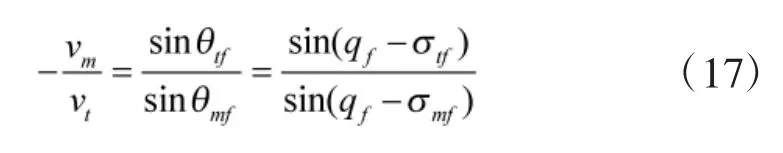
令

得到
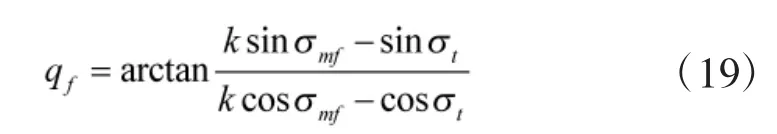
将式(15)、式(19)代入到式(14)中得到aB的最终表达式为
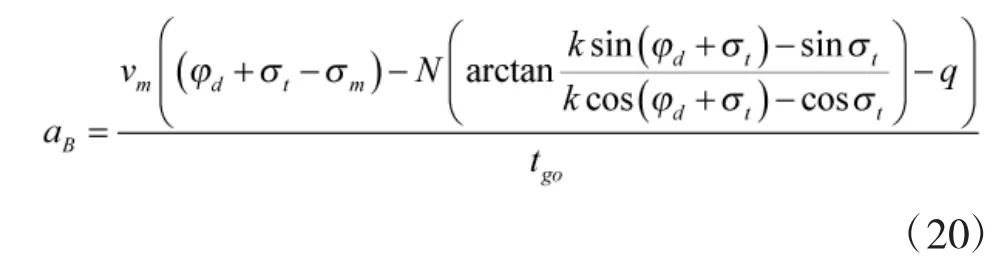
将式(20)代入到式(10),则攻击运动目标带落角约束偏置比例导引律的制导方程为
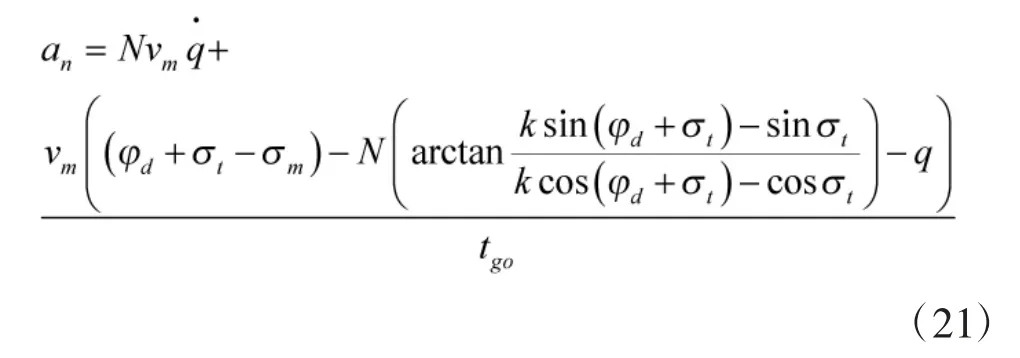

2 基于预测碰撞点的剩余飞行时间估计
基于预测碰撞点的剩余飞行时间估计的核心思想是通过预测出弹目碰撞点,然后按照攻击静止目标的剩余飞行时间估算方法进行估计[14]。因此,最后的估计准确与否与以下两步有关:1)攻击静止目标带落角约束的剩余飞行时间估计准确与否。2)弹目碰撞点预测的准确与否。
考虑导弹攻击运动目标情况,假设最终攻击点为P,导弹攻击运动目标的示意图如图2 所示。
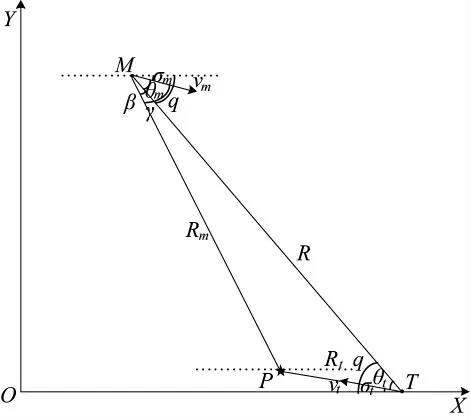
图2 导弹攻击运动目标示意图
根据文献[5]攻击静止目标得到的结论,则导弹直接攻击位于预测碰撞点P 的静止目标时的剩余飞行时间为

式中,Rm为导弹到预测碰撞点的距离,γ 为导弹速度方向与Rm的夹角,β 为Rm与初始弹目视线R 的夹角。因为Rm,γ,β 未知,下面要做的工作是用已知量代替。
在△MTP 中,根据几何关系,有
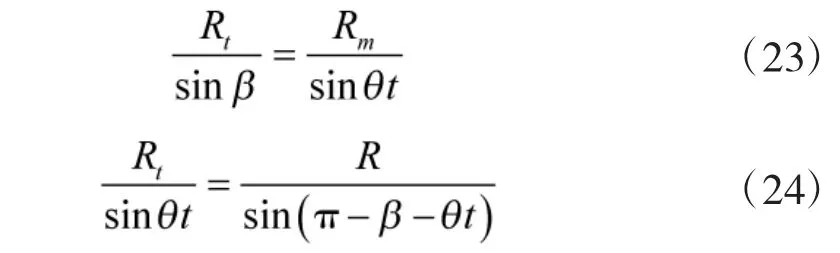
在β 和θt为小值时,式(23)、式(24)可以简化为


在目标做匀速直线运动的前提下,有

为了便于计算,令

将式(22)、式(27)、式(28)代入式(25),化简后按照泰勒级数方法展开并取有效值为
这些问题制约着高等职业教育的发展,需要根据市场变化和社会与经济的发展进行改革,深化工学结合,建立以职业能力培养为核心的高职教育人才培养模式。

将式(30)代入到式(27),化简得

根据图2 中的几何关系,有

将式(29)、式(30)、式(31)代入到式(22),最终得到基于预测碰撞点的带落角约束的剩余飞行时间估计为
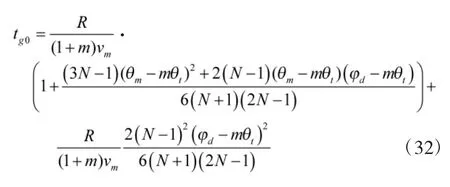
3 仿真结果与分析
假设用导弹攻击地面运动目标,基本参数设置如下:导弹和目标的初始位置分别为(5 000 m,5 000 m),(10 000 m,0 m);导弹和目标的速度恒定,分别为vm=300 m/s,vt=30 m/s;比例系数N=3。导弹的初始导弹倾角为0°,目标的倾角设置为0°,期望导弹落角为-30°;分别用传统剩余飞行时间估计方法,文献[5-6]得到的剩余飞行时间估计方法和本文得到的剩余飞行时间方法代入本文推导得到的制导律,得到仿真结果如表1 和图3、图4 所示。
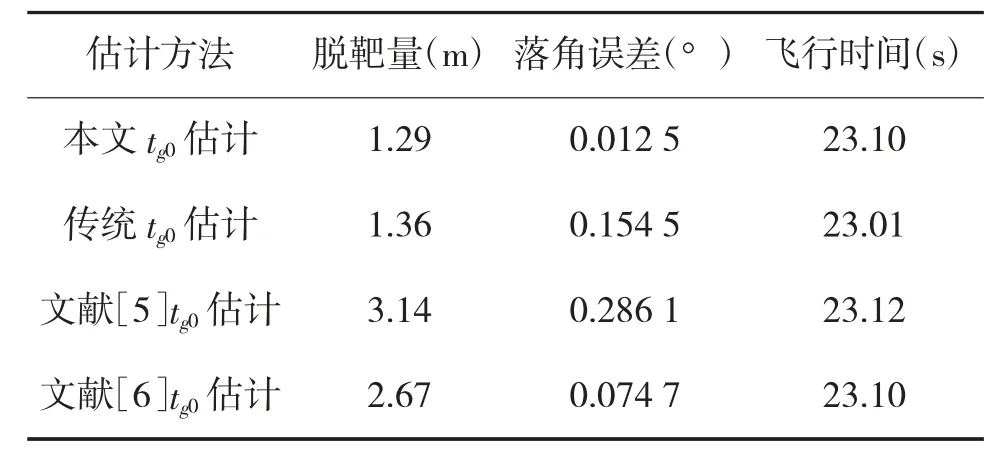
表1 不同剩余飞行时间下导弹参数
从表1 中可以看出,在本文设计的剩余飞行时间下脱靶量和落角误差最小,尤其对落角的控制能力要明显好于其他3 种剩余时间估计。从图3 和图4 中可以看出,本文的剩余飞行时间估计精度要优于其他3 种剩余时间估计,传统估计方法次之,因为文献[5-6]中的剩余飞行时间估计是在特定的制导律下设计的,因此,不适用于本文推导得到的制导律。下面将研究将本文得到的基于预测碰撞点的剩余时间估计tg0代入本文设计的攻击运动目标的带落角约束偏置比例导引律的性能。
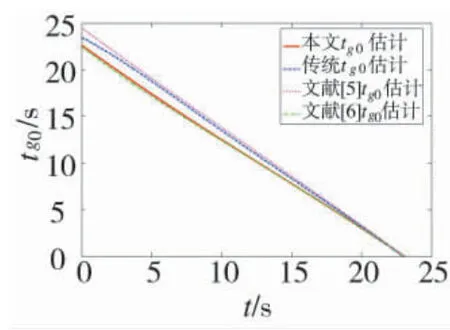
图3 剩余飞行时间变化曲线
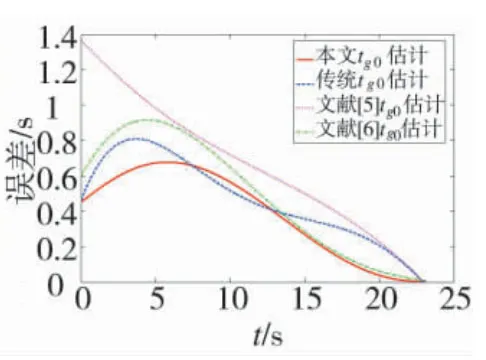
图4 剩余飞行时间误差变化曲线
假设导弹攻击地面带倾角运动目标,设置目标倾角为σt=20°,导弹和目标的其他基本参数设置同上。设定制导盲区距离为20 m,导弹进入制导盲区后按进入制导盲区瞬时的法向过载飞行。将本文设计的基于预测碰撞点的剩余时间估计tg0代入本文推导的攻击运动目标带落角约束的偏置比例导引律,仿真得到导弹主要特征变化如图5~图8 所示。
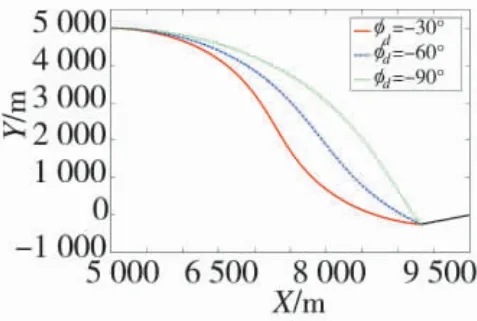
图5 导弹和目标轨迹

图6 弹道倾角变化曲线

图7 过载变化曲线
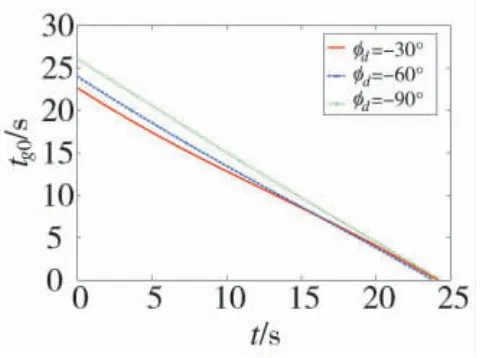
图8 剩余飞行时间变化曲线
从图5~图6 中可以看出,本文设计的攻击运动目标带落角约束的偏置比例导引律在不同的期望落角条件下都可以击中目标且满足落角约束;从图7 中可以看出,不同的期望落角条件下的过载都在合理的范围内,且随着期望落角的增大,过载减小。从图8 中可以看出期望落角为-60°时飞行时间最短,期望落角为-90°时飞行时间最长,且不同期望落角下剩余飞行时间估计误差不同,这是由于在不同的期望落角下弹道的长度和曲率不同造成的。
仿真得到的具体参数随时间的变化如表2所示。

表2 不同期望落角下导弹参数
从表2 中可以看出,本文设计的攻击运动目标的偏置比例导引律在不同的期望落角条件下脱靶量和落角误差都较小,过载维持在合理的区间内。可以得到结论:本文设计的攻击快速运动目标带落角约束的偏置比例导引律较文献[8]设计的偏置比例导引律脱靶量和落角误差有了显著的减小,且过载方面有了明显的改进,可以实现对带倾角运动目标的指定角度攻击。
4 结论
本文推导了攻击运动目标带落角约束的偏置比例导引律,并在该偏置比例导引律下设计了基于预测碰撞点的剩余时间估计方法。通过与3 种不同剩余飞行时间估计方法的比较,验证了在本文推导的导引律下,本文设计的剩余飞行时间估计方法更精准;将本文设计的tg0估计方法代入本文设计的导引律进行仿真验证,结果表明:本文设计的导引律可以指定角度攻击带倾角运动目标,对于攻击复杂地形下的坦克、地面装甲车等带倾角运动目标,具有一定的实际应用价值。

