基于SAR 目标识别的深度学习方法*
郝 岩,白艳萍,张校非
(1.中北大学信息与通信工程学院,太原 030051;2.中北大学理学院,太原 030051)
0 引言
合成孔径雷达(SAR)以其自身的独特优势而被广泛应用于军事和民用领域。目前,SAR 目标识别技术主要包括基于支持向量机的目标识别技术[1];基于模板的目标识别技术[2]以及基于神经网络的目标识别技术[3-6]。其中基于神经网络的目标识别技术应用最为广泛,尤其是BP 神经网络。但BP 反向传播过程中,局部梯度下降对权值进行调整容易出现梯度弥散,导致局部最优问题。而且,随着网络层数的增多,这种情况会越来越严重。这一问题的产生严重制约了神经网络的发展。
2006 年,Hinton 提出对深度学习方法以及模型训练方法的改进打破了BP 神经网络发展的瓶颈,由此引发了新一轮的深度学习浪潮。深度学习方法主要包括3 类[7]:1)生成模型:常见的生成模型包括,RBM(受限玻尔兹曼机)、AE(自编码)及其各种变型。2)判别模型:CNN(卷积神经网络)是一种良好的判别模型,成功应用于多类图像的分类研究中,也是一种非常成熟的深度学习方法。3)混合模型:即包含了生成和判别两部分结构的模型,例如DBN(深度信念网络)或SAE(栈式自编码)预训练后的DNN(深度神经网络)。本文主要研究DBN 以及SDAE(栈式降噪自编码)无监督预训练,BP 神经网络“微调”的两种混合模型。
目前,大多数人选用的DBN 或SDAE 都具有两个或两个以上隐含层,但随着隐含层和神经元数量的增多,计算复杂度自然会增大,训练耗时较长。另外,虽然两种深度学习方法都可以自动提取图像的高级特征,但SDAE 是非线性变换找到主特征方向,而DBN 是基于样本的概率分布来提取高层表示,所提取的特征具有很大差异,依然存在特征利用不充分从而造成识别效果较差的问题。本文针对这两个问题,提出了一种双通道单隐含层的DBN-SDAE 模型,通过DBN 和SDAE 分别学习数据的深层特征,然后采用加权融合法融合二者所学习的权重,用以初始化NN 的权值。该模型不仅可以降低计算的时间复杂度,还可以得到相当可观的识别准确率。
1 算法原理
1.1 深度信念网络(DBN)
深度信念网络是一种混合模型,包括无监督的预训练和“微调”两部分。一个DBN 被视为由若干个RBM 堆叠在一起,训练时可通过由低到高逐层训练这些RBM 来实现。
RBM(受限玻尔兹曼机)由可见层和隐含层构成,层内无连接,层间全连接。其目标是尽可能使可见层分布逼近样本空间的分布,换句话说就是使得训练样本在该模型中的观测概率最大,这个目标可以通过最小化KL 距离[8]实现,详细过程见文献[9-10]。
对于一个RBM 模型,如图1 所示,由于RBM是一个随机网络,无法确定该模型的分布函数,因此,通过能量模型来得到模型的分布,其能量模型定义为
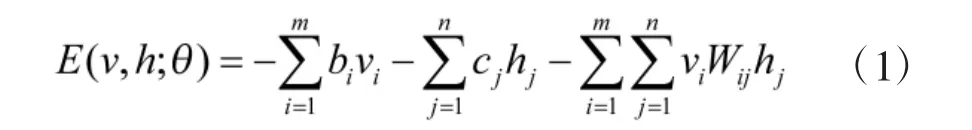
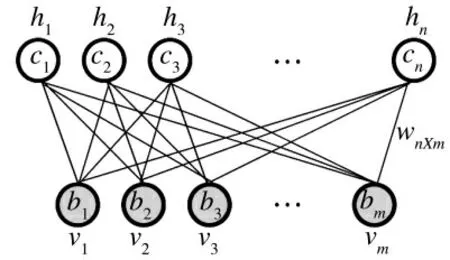
图1 RBM 结构图
其中,v 和h 分别表示可见层和隐含层,vi表示第i个可见单元,hj表示第j 个隐藏单元,bi和cj分别表示vi和hj的偏移量,Wij为vi和hj之间的权重。θ={Wij,bi,cj}为RBM 模型的参数。则基于上述能量模型可得到相应的联合概率分布:
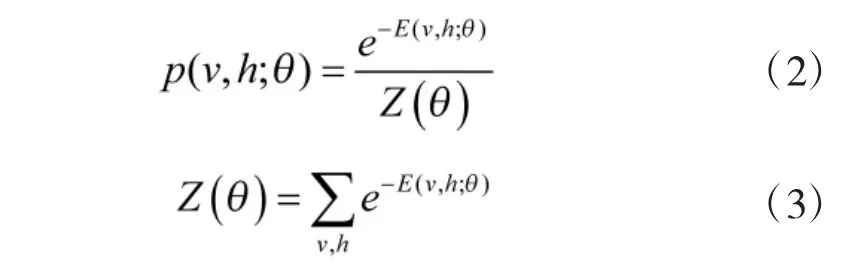
Z(θ)为归一化因子,也称为配分函数。
在实际应用中,如何确定由RBM 模型所定义的观测数据的分布是关键问题,因此,需要计算v 的边际概率:
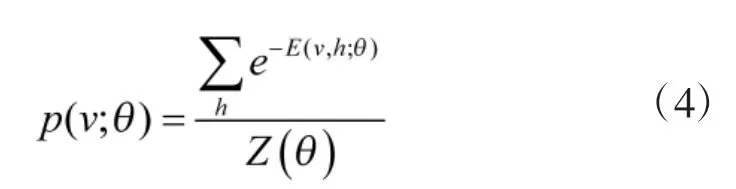
由此,可以通过最大化p(v;θ)在训练集上的对数似然来获得θ。通过CD[11](对比散度)快速学习方法得到最终的W,b,c。
其过程如下:
可见层:v:v1=x,x 为训练样本;
1.2 栈式降噪自编码
栈式降噪自编码是指由降噪自编码(DAE)[12]堆叠而成的深层神经网络,DAE 与自编码器(AE)的不同之处是在原始数据上加入噪声,然后将含噪声的数据作为网络的输入数据,来重构输出原始还未加入噪声的数据。下面简单介绍一下AE。
图2 是自编码器的结构示意图,图中,x1,x2,x3,x4表示网络的输入单元,h1,h2,h3表示网络的隐藏单元,y1,y2,y3,y4表示x1,x2,x3,x4的重构,+1 表示偏置项。
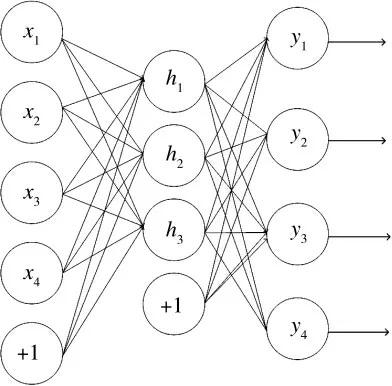
图2 自编码器的结构示意图
自编码神经网络主要可以分为两个过程,编码和解码。其基本思想是将输入样本压缩到隐藏层,再在输出端重建样本。
具体过程如下:
W1是输入层与隐含层之间的权重,W2是隐含层与重构单元之间的权重,b1,b2分别是输入层和隐含层的偏置。另外,SDAE 的训练过程与DBN 的训练过程相似,均采用贪婪学习法,这里不再叙述。
2 DBN-SDAE 简介
对于传统的深度学习方法,隐含层和神经元越多,自动学习到的高阶特征越多,通常情况下,第1个隐含层学习输入数据的一阶特征,而第2 个隐含层会学习到二阶特征,如轮廓或角点,其他的隐含层则会学习更加复杂的高阶特征。但随着隐含层和神经元数量的增多,网络的计算复杂度会呈指数增长,耗时更长。同时由于DBN 和SDAE 算法的差异,各自学习的特征也有所差异,往往会出现特征利用不充分的情况。为了避免上述问题,本文提出一种双通道单隐含层的深度学习方法,并采用加权融合的方法进行特征融合。为了得到更好的识别效果,本文采用BP 神经网络进行微调。其结构如图3 所示。
算法步骤如下:
1)对数据进行预处理,并将处理好的数据分为训练样本和测试样本;
2)将训练样本分别输入单隐层的DBN 和SDAE,通过自动学习得到各自学习后的权重;
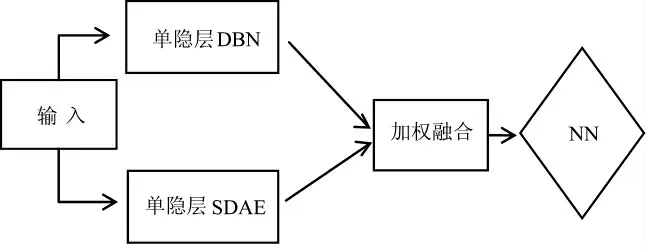
图3 DBN-SDAE 模型示意图
3)对权重进行加权融合,并用融合后的权重初始化NN 的权重;
4)将训练样本和测试样本输入NN,通过BP进行“微调”,最终分类。
对DBN 和SDAE 学习的权重加权公式定义如下:
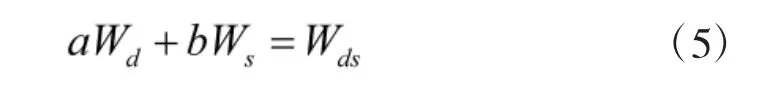
其中,Wd为DBN 学习得到的权重,Ws为SDAE 学习得到的权重,Wds为二者加权后得到的权重。a,b分别为二者的加权系数,且a,b∈[0,1],a+b=1。选择加权系数时,首先确定最优系数的范围,然后对系数进行细化,具体见实验部分。
3 实验及结果分析
3.1 数据预处理
本文的实验数据选自MSTAR 的公开数据集,选取BMP2(装甲车),BTR70(装甲车)以及T72(主战坦克)作为目标。实验分别选取SN_C21,SN_C71和SN_132 俯仰角下的图像作为训练样本,共698个,15°俯仰角下的图像作为测试样本,共588 个。数据库中的SAR 图像分辨率为0.3 m×0.3 m,目标图像大小为128×128 像素。由于这些图像的目标均集中于图像的中间部分,因此,本文首先将图像中心部分剪裁为64×64 的图像。同时为了减小噪声对目标识别的影响,本文采用Gaussian 去噪法对图像进行去噪处理。处理过程见图4。将处理过的图像张成列向量,则训练样本为4 096×698,测试样本为4 096×588。
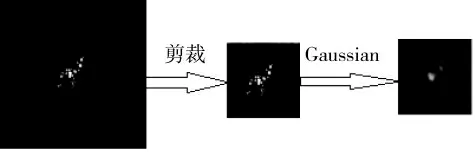
图4 图像预处理过程
3.2 网络参数设置
为了保证与下文实验的一致性,DBN 和SDAE均采用批量训练的方法,且只有一个隐含层。
在DBN 网络中,可见单元的数量为4 096,隐藏单元的数量为100,训练次数设置为50,批量大小为2,相应的BP 神经网络的结构为4 096-100-3,训练次数为1 500。
在SDAE 网络中,输入层和隐含层单元数量分别为4 096,100,训练次数为100,批量大小为2,相应的BP 神经网络的结构为4 096-100-3,训练次数为100。两个网络的其他相关参数见表1。

表1 DBN 与SDAE 其他参数设置
3.3 实验
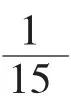

图5 网络对应的特征图
从图5 中可以明显看出,DBN 所学习到的特征细节信息较多,结构信息不明显,而SDAE 学习到的特征既包含了细节信息又包含了结构信息,且结构信息较多。因此,SDAE 比DBN 获得了更好的识别效果。
通过上述实验可以发现,DBN 可以提取更多的细节信息,而SDAE 则能提取到结构信息。因此,本文选择将两种方法学习的特征进行加权融合。同时为了降低时间复杂度,DBN 和SDAE 均采用单隐含层,通过对DBN 和SAE 学习的权重进行加权融合,进而初始化NN 神经网络的权值。表2 是加权平均的系数及最佳识别效果。
从表2 可以看出,随着DBN 权重所占比重的增大,除了序号为3 和9 的两组实验,识别准确率基本上呈逐渐降低的趋势。且DBN 权重比例超过0.5后,其识别准确率低于DBN 的识别准确率。另外,达到最佳识别准确率的迭代次数均维持在0~130 之间(不包括序号为1 和11 的两组实验),但随着DBN 权重所占比例的增大,达到最佳识别准确率的迭代次数也有所增加,但相比于单一的单隐含层DBN,迭代次数大大减少。从表2 还可以看出,当SDAE 的系数为0.8 时,最佳识别准确率最高,可达到98.469%,高于单隐含层的DBN 和SDAE。
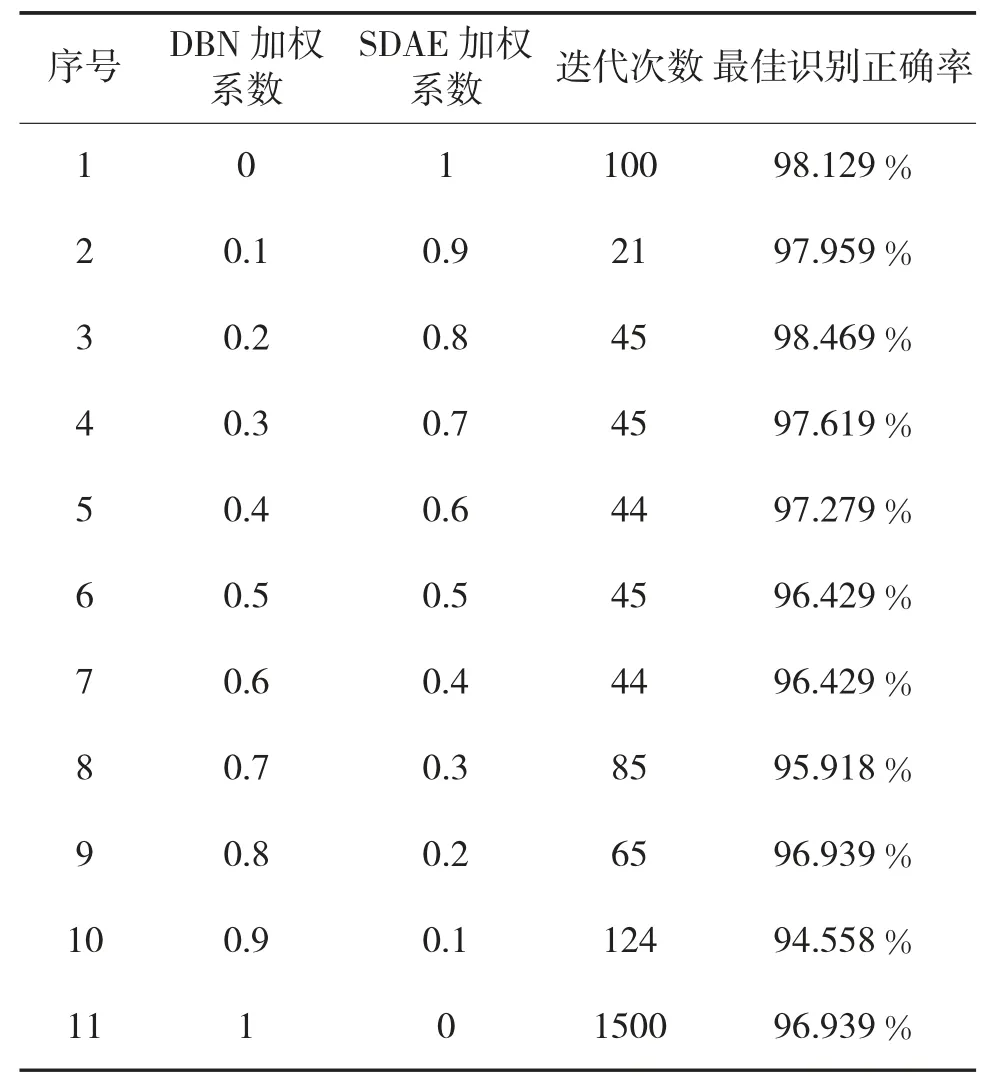
表2 加权系数及最佳识别准确率
为了进一步体现最优的加权系数,根据表2 的结果,SDAE 的最优系数应处于0.8~1 之间。下页表3 是细化后的加权系数及最佳识别准确率。
对于细化后的结果进行分析发现,SDAE 加权系数在0.8~1 之间的识别准确率均在97 %以上,且当SDAE 系数为0.81,DBN 系数为0.19 时识别准确率最高,可达到98.640%,较单隐含层的SDAE 和DBN 分别高出0.511%及1.701%,充分证明了本文所提方法的有效性。
4 结论
本文针对SAR 目标识别问题,研究了DBN 及SDAE 两种深度学习模型。并针对传统的深度学习存在的问题:1)随着隐含层数和神经元数量的增加,计算复杂度呈指数增长;2)深度学习方法虽然可以提取图像的高阶特征,但依然存在特征利用不充分的问题;提出了一种双通道单隐含层的模型DBN-SDAE。该模型不仅解决了上述两个问题,还实现了较可观的识别准确率,最高可达到98.640%,且加权融合后的识别准确率均高于单一的单隐含层DBN 或SDAE 模型,充分证明了所提方法的有效性。
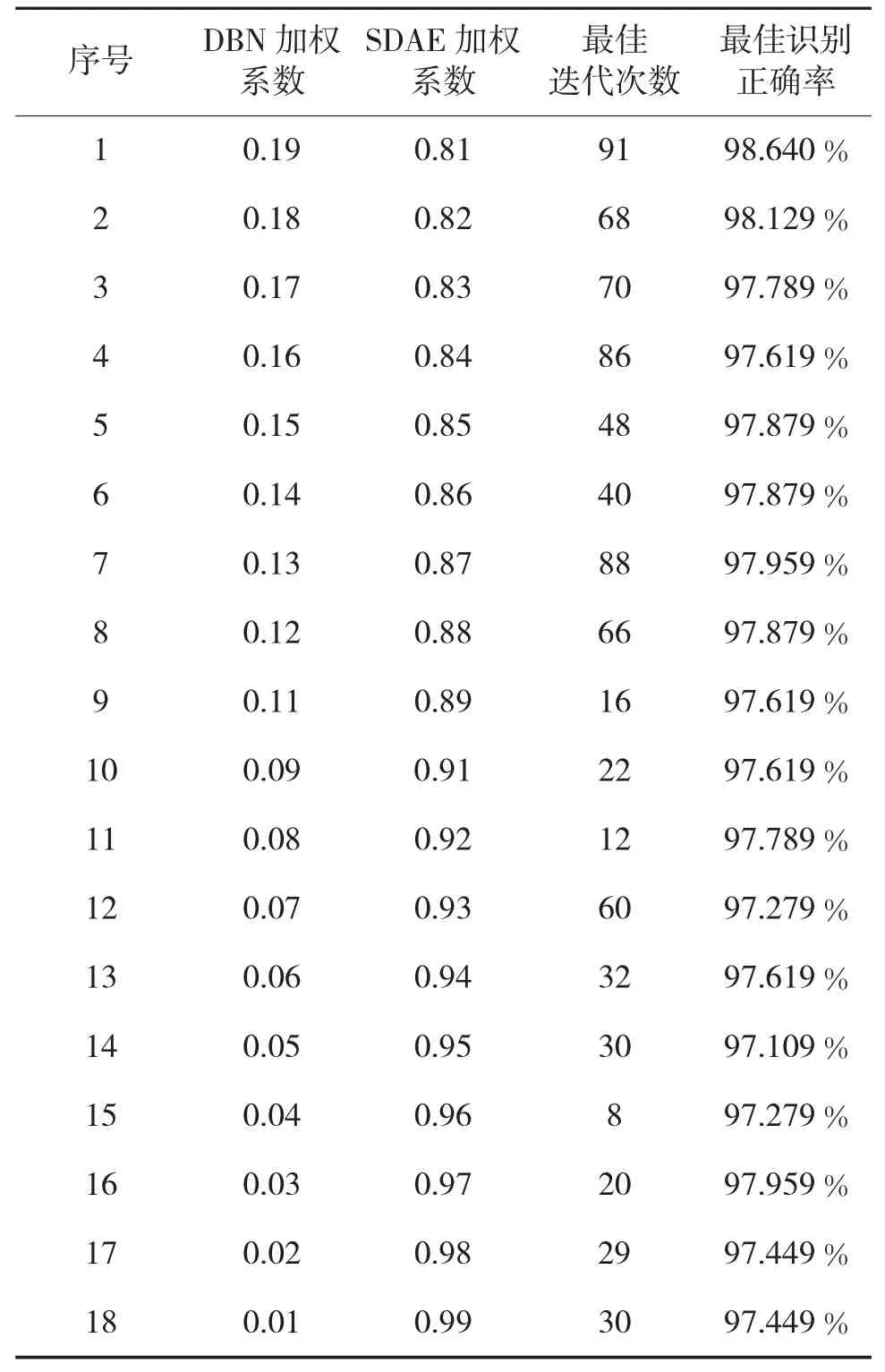
表3 细化后加权系数及最佳识别准确率

