光电稳定平台中Stribeck 摩擦力矩的补偿方法*

韩小康，董 浩，王 明，金敬强，董祺宁，张 雷

（北方自动控制技术研究所，太原 030006）

0 引言

光电稳定平台是一种高精度的稳定系统，可以实现对地、对空目标的大范围全景式探测。其主要功能是隔离载体角运动，保持平台指向准确、朝向稳定。由于摩擦力矩等非线性干扰的存在［1］，容易产生滞滑爬行等现象，影响系统稳定性。

目前，针对光电稳定平台的稳定控制，学者们提出了众多方法。针对稳定系统中的非线性扰动，Li B，Hullender D，Derenzo M［2］采用LQG 和Kalman滤波算法对扰动进行实时估计和补偿，并采用自校正控制的方法以提高LQG 算法的鲁棒性，结果表明，这种算法相比于传统的PI 算法精度提高了近一倍；王合龙，刘建业［3］提出的基于线性自适应神经网络原理的改进算法，可以有效抑制线性扰动对平台的影响，但是对非线性扰动的抑制效果不佳；李贤涛，张葆等人［4］提出的自抗扰扰动器可对扰动进行估计和补偿。但是这些算法计算量大，计算复杂，或依赖被控对象的精确数学模型，工程实现较难，由于库伦摩擦、静摩擦、粘滞摩擦等各种非线性扰动的存在，系统采用经典控制很难保证平台的稳定精度，因此，需要一种可以有效抑制非线性扰动的控制方法。

滑模变结构控制能够通过控制器本身结构的变化，突破经典线性控制系统的限制，用滑模变结构控制方法来研究非线性系统的鲁棒问题，易于工程实现［5］。本文提出采用指数趋近律的滑模变结构的方法，将其用于速度环进行仿真分析，并与速度环为经典PI 算法的系统进行比较。

1 双闭环调速系统模型建立

1.1 建模与分析

直流电机双闭环控制系统的结构图，如图1所示。

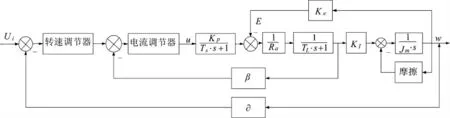
图1 双闭环控制系统的结构图

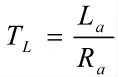
系统的状态空间模型可以写为

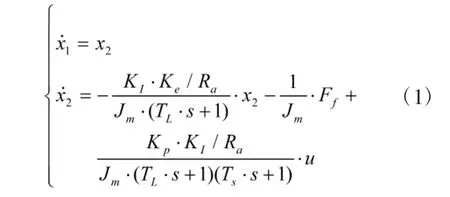
通过式（1）可得，Ff为摩擦力，x1（t）=θ（t）为转角，x2（t）=ω（t）为角速度，对于直流电机双闭环调速系统状态方程描述如下：

式中，

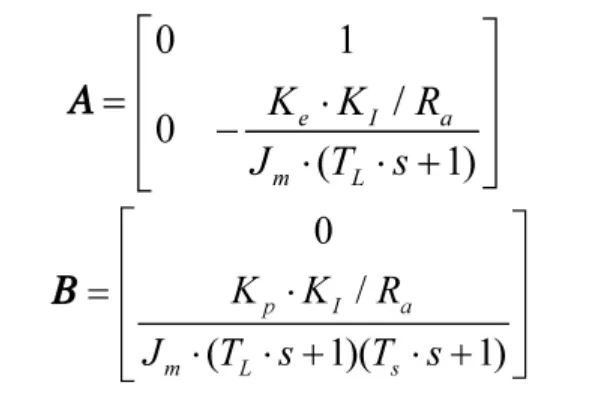
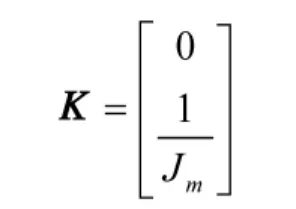
1.2 Stribeck 摩擦

摩擦是一种复杂的现象，对摩擦模型的研究经历了相当长的时间。传统的leonarndo Da Vinci 模型是假定摩擦力的大小正比于负载质量，与运动方向相反，与接触面无关。目前工程中经常采用的有库伦摩擦模型、库伦+粘滞摩擦模型、静摩擦+库伦摩擦+粘滞摩擦模型及Stribeck 摩擦模型。Stribeck摩擦模型相较于上述3 种摩擦模型都更接近工程实际。

Stribeck 摩擦力曲线，如图2 所示。

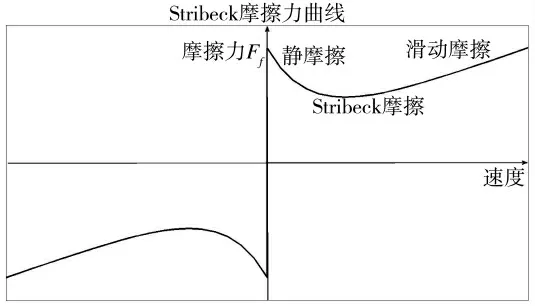
图2 Stribeck 摩擦力曲线

Stribeck 等人通过实验观察得出，物体从静止到运动的过程中，摩擦力的变化实际上是连续的。低速运动时，摩擦力矩随角速度的增大而减小的效应，称为Stribeck 效应［6］，相应的模型称为Stribeck模型。其表达式为

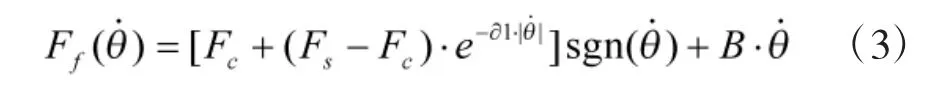
式中，Fc为库伦摩擦力，Fs为最大静摩擦力，B 为粘滞摩擦系数，θ˙为输出角速度，∂1为经验常数。

2 滑模变结构控制

2.1 滑模变结构控制原理

变结构控制（variable structure control，VSC）出现于20 世纪50 年代，因为它的控制是不连续的，所以本质上它是一类非线性控制。这种控制策略的特点是，在产生控制作用的动态过程中系统的结构是可以有目的地不断变化的，系统当前的各种状态是这种变化的依据，它们迫使系统按照预定的“滑动模态”轨迹进行运动，因此，变结构控制也被称为滑动模态控制（sliding mode control，SMC）即滑模变结构控制。滑模变结构控制具有很多优点，诸如响应比较快，鲁棒性好，物理实现简单等，这些都得益于滑动模块可以进行设计且与对象参数及扰动无关的特点。

2.2 滑模变结构控制器设计

滑模变结构控制的设计就是需要确定切换函数s（x）（x∈Rm），以求解控制函数：

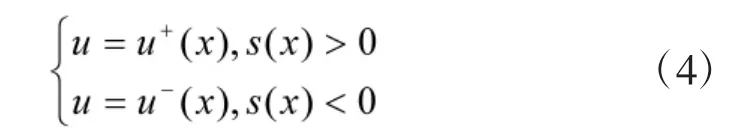
1）滑动模态存在；

2）满足可达性条件，即在切换面以外的点可以在有限时间内到达切换面；

3）保证滑模运动的稳定性；

4）达到控制系统的动态品质要求。

设转速控制器输入误差方程为

式中，∂为转速环反馈系数，ω 为转速。

设滑模面为

对式（6）求导，得到

由于

将式（8）代入式（7）中得

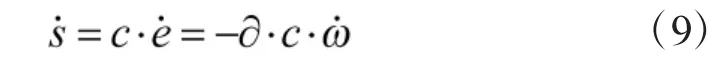
指数趋近律具有加快趋近时间、削弱抖动的功能，取指数趋近律如下

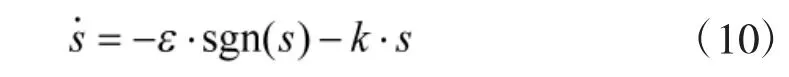
式中，ε>0，k>0。

当运动点远离切换面时，趋近速度主要取决于-k·s项；当到达切换面时，趋近速度主要取决于-ε·sgn（s）项，因此，k 取值较大，ε 取值较小。

滑模控制律的求取目标是为使系统在有限时间内到达滑模面上并保持稳定，联立式（9）与式（10）可得

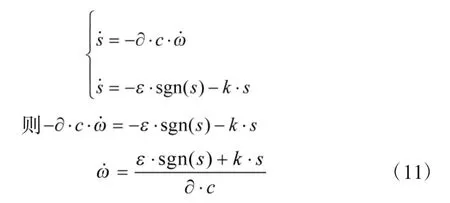
根据式（1）可知

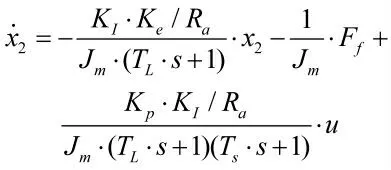
因此，

将式（11）代入上式得到控制律

利用李雅普诺夫稳定性理论，取李雅普诺夫函数

对式（10）求导得到

由李雅普诺夫稳定判据可知，设计的滑模变结构控制器满足稳定性要求。

3 仿真研究

假设某型光电稳定平台的载体相对于惯性空间以0.65 rad/s 的角速度转动，此时转速环的输入误差为10 V，若想使得平台相对于惯性空间朝向稳定，需要使平台沿着与载体相反的方向运动以抵消载体的角速度。

假设电机电枢电阻Ra=5 Ω，电机时间常数TL=0.01 s，电机力矩系数KI=0.2 N·m/A，反电动势系数Ke=2 V/A，转动惯量Jm=0.013 kg·m2，惯性时间常数Ts=0.003 s，放大系数Kp=3。库伦摩擦力0.01 N·m，最大静摩擦力0.03 N·m，粘性摩擦系数0.02，∂1=3得到Stribeck 波形，如图3 所示。

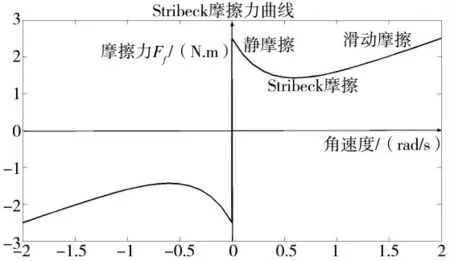
图3 某型光电稳定平台中的Stribeck 摩擦力

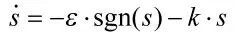
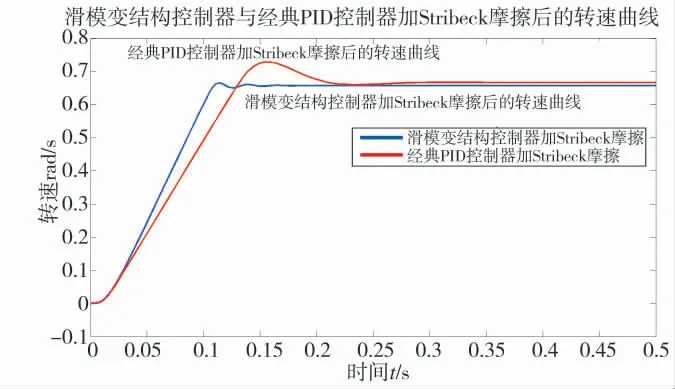
图4 滑模变结构与经典PI 抑制摩擦对比图

由图4 可知，光电稳定平台相对于载体最终的稳定转速为0.65 rad/s，滑模变结构控制器的超调量为0.01 rad/s，经典PI 控制器的超调量0.07 rad/s，滑模变结构控制器的调节时间为0.16 s，经典PI 控制器的调节时间为0.23 s，滑模变结构控制器相比于经典PI 控制器，上升时间更短，超调更小。

由图5 可知，对于转速环中10 V 的输入误差，滑模变结构控制经过0.13 s 将其补偿为零，而经典控制经过0.27 s 才能将其补偿为零。

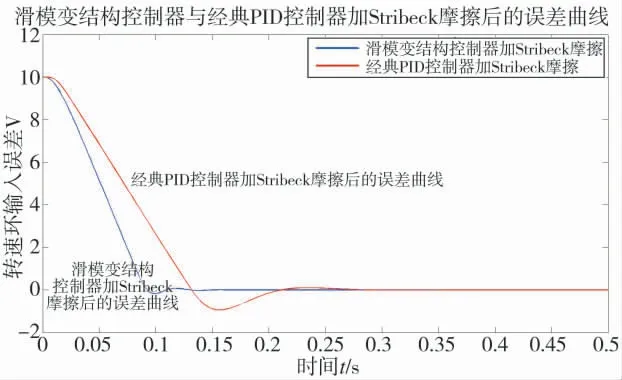
图5 转速环输入误差的对比图

4 结论

本文通过对光电稳定平台中控制系统的建模，建立转速电流双闭环控制系统的仿真模型，在转速环中使用滑模变结构控制器对Stribeck 摩擦力矩进行补偿。通过仿真分析可知，滑模变结构控制的超调量为0.01 rad/s，而经典控制的超调量为0.07 rad/s，滑模变结构控制的调节时间为0.16 s，而经典控制的调节时间为0.23 s；同时，对于载体扰动，滑模变结构控制的补偿时间为0.13 s，小于经典控制的补偿时间0.27 s。因此，相比于经典PI 控制，滑模变结构控制的上升时间更短，超调更小，对光电稳定平台Stribeck 摩擦的补偿效果更好。