基于改进PH 曲线的无人机路径规划方法*
张建东,车冰凌⋆,杨啟明,郭 操
(1.西北工业大学电子信息学院,西安 710072;2.沈阳飞机设计研究所,沈阳 110035)
0 引言
随着作战任务复杂度的提高,提升无人机自主作战能力成为当前研究重点,对于无人机航路规划方法的研究已经形成了不少较为成熟的方法。例如:A*搜索算法[1]、图搜索[2]、动态规划法、人工势场法等。这类方法通常缺乏对无人机机动性能约束,忽略了航迹的整体平滑和曲率约束的需求。
为了能让所规划的路径能够平滑可飞,应将适用于无人机飞行的曲线直接应用于无人机的路径规划中。文献[3]将Dubins 路径应用于智能车路径规划问题,结合PID 控制理论对路径曲线进行控制;文献[4-10]将PH 曲线用于路径规划,分别结合模拟退火算法(SA)、遗传算法(GA)、粒子群算法(PSO)、蚁群算法(ACO)、人工蜂群算法(ABC),调节曲线参数,获取一条符合安全性、机动性约束的最优PH 路径。但在实际复杂战场环境中,障碍威胁并不总是易于发现的,仅仅将一条PH 曲线作为全局规划航路,难以灵活应对突发危险,并且每更改一处障碍都可能导致整条航迹重新规划,是对无人机资源的浪费。
本文针对现有无人机路径曲线规划的不足,在有威胁障碍的复杂环境中,基于改进的PH 曲线,提出一种组合多段PH 路径的无人机航迹规划方法,能够灵活应对复杂突发威胁,实现避障的同时,保证无人机航迹的曲线、曲率连续性。
1 基于PH 曲线航迹规划
路径规划的目的是得到一条安全的飞行路线。由于无人机的机动特性约束,要求规划航迹必须满足航迹曲线连续以及航迹曲率连续。PH 曲线是具有有理特性的参数化曲线,具有弯曲能量小,曲率和长度均有闭合解等优势,能够满足曲率连续变化的约束[11]。具有连续曲率的PH 曲线[12]可以应用于无人机路径规划。对于一般路径曲线,以q 为参数的路径r(q)的长度可写成如下形式:
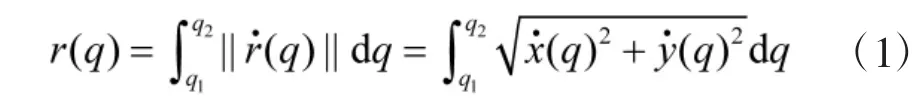
PH 路径曲线由于矢端矢量满足勾股条件,路径长度具有闭合解。因此,对路径长度的求解可以简化为对多项式的积分:

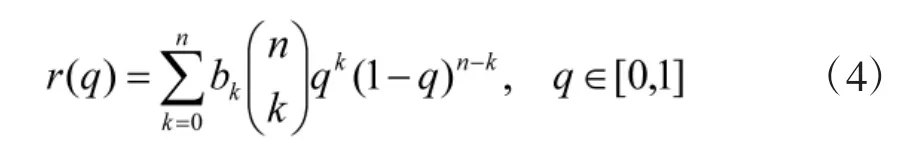
2 PH 路径筛选
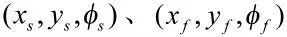

曲线能量计算过程较为繁琐,为简化筛选流程,本文提出一种通过比较PH 曲线与对应Dubins 路径的形状一致性的方法,实现对PH 路径曲线的筛选。已知两位姿点之间的最短路径是Dubins 路径[16],因此,曲线形状最接近Dubins 路径,则可以认为具有最短路径长度的优势。Dubins 路径可以简单定义为:在最大曲率限制下,平面内两个位姿点之间的最短可行路径是CLC 路径或者CCC 路径,或者是它们的子集,其中C 表示弧段,L 表示与C 相切的直线段,不失一般性,本文中仅考虑CLC 路径。
对于构造PH 曲线,任意两个位姿点,都可以出现4 种可行解,通过解析几何方法,可以构造出4 种Dubins 路径曲线,从中选出最短路径如图1 所示:
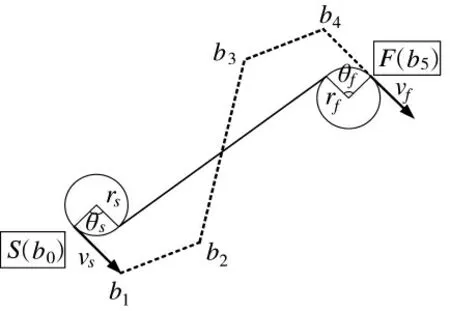
图1 PH 曲线筛选示意图
其中,θs表示第1 个C 弧段夹角,θf表示第2 个C 弧段夹角,bi为PH 曲线控制点,选取PH 曲线与Dubins 路径形状具有一致性。
无人机执行任务时,可以认为无人机始终朝向任务目标点方向运动,路径规划中不会出现超过180°大的转弯角度。在初、末转弯半径近似相等的情况下,要获得最短Dubins 路径,尽可能选择C 弧段对应角度最小的路线。在机动条件下,可以验证本文所提出关于PH 路径筛选方法的正确性。
3 多路径合成
复杂战场环境中进行航路规划[17-19],既要满足安全性、机动性约束、路径最短,还要尽可能保证规划航路具有灵活性、实时性,仅由一条PH 曲线作为全局规划航路显然是不合理的,因此,有必要针对复杂环境进行区域划分,对多段PH 曲线进行合成,以获得一条满足要求的规划航路。
3.1 贪心算法路径选择
贪心算法(greed algorithm),基于在每一步作出最佳选择,获取局部最优解,通过每一步的最优选择可以得到全局最优解。
3.1.1 贪心选择策略
由两位姿点可以得到一条最短的Dubins 路径,存在两种情况如图2 所示,分别对应以下两种策略:
1)当规划路径不与障碍物相交,则使用当前路径;2)当规划路径与障碍物相交,将路径拆分,得到新的两条Dubins 路径,组合成为新路径。
获取新路径原则:由两条路径构成的新路径与原始路径需位于障碍圆的同侧,由上一节关于最短Dubins 路径筛选方法的讨论,经过障碍圆的弧段部分对应的夹角最小,则路径最短。贪心选择策略得到的两段路径组合是最短路径,满足单步最优条件。
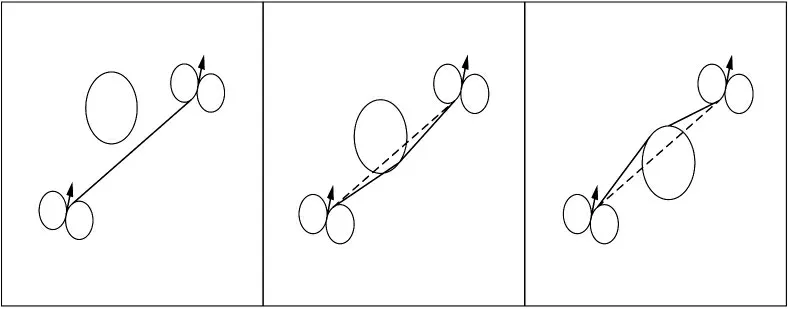
图2 贪心选择策略示意图
3.1.2 最优子结构
采用自下而上(或者自上而下)单向寻优。假设初始路径中不存在障碍圆,得到一条Dubins 路径,之后按照由近及远的顺序加入障碍圆,每加入一个障碍,按照贪心选择策略进行择优,然后将原问题转变具有同样性质的子问题,从新的起始位姿点到终点的路径寻优。不断作出贪心选择,最终得到全局最优组合结果。
3.2 PH 多段路径合成改进算法
通过贪心策略可以得到一系列位姿点,从而获得多段PH 路径,若要得到全局路径,需要将其组合。如果直接将曲线首尾相连,得到的组合路径曲线连续,曲率不连续。为了解决这个问题,本文对PH 曲线方法进行改进:
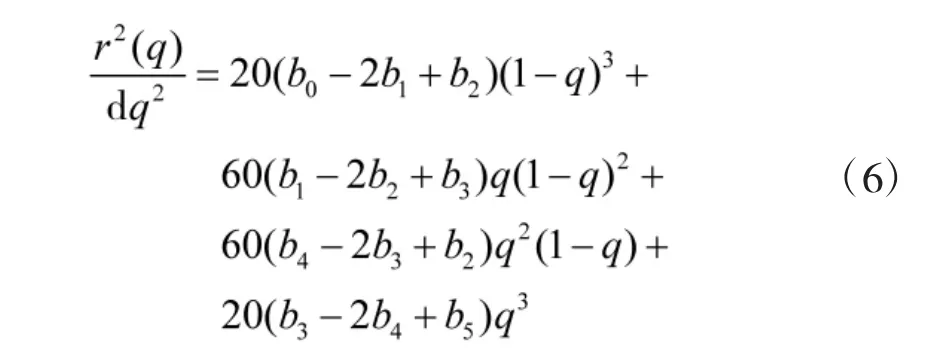
对于5 次PH 多项式,由式(6)可以发现,r(q)具有对称性,曲率κ 取决于r(q)的一、二阶导数,当q=1,一阶导数值只与参数b4,b5有关,二阶导数值只与参数b3,b4,b5有关;当q=0,一阶导数值只与参数b1,b0有关,二阶导数值只与参数b2,b1,b0有关。因此,连续两条PH 曲线,只要前一条曲线的参数b3,b4,b5与后一条曲线的参数b2,b1,b0满足对称关系,就可以保证多段曲线连接点处曲线、曲率连续。改进算法步骤如下:
1)给出第i 组初、末位姿点,构造PH 曲线;
2)使用动态优化方法调整单条曲线参数,控制PH 曲线曲率与长度;
3)给出第i+1 组初、末位姿点,首先构造PH 曲线,然后将控制参数b2,b1替换为第i 组位姿点曲线参数b3,b4的对称点,即可得到修正后的曲线;
4)重复步骤1)、2)、3)直到得到完整曲线。
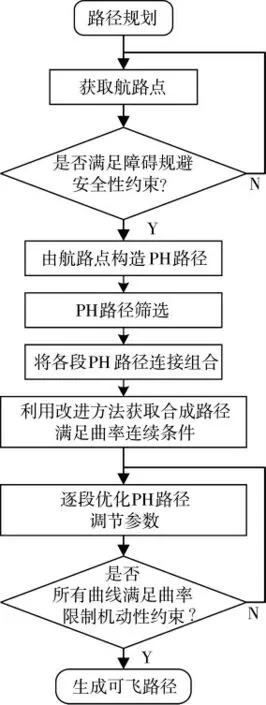
图3 多路径组合规划方法流程图
4 实验仿真
设置无人机战场环境空域大小为100 km*50 km,对本文提出的无人机航路规划方法在MATLAB 环境下进行仿真验证。设定无人机初始位姿点,末位姿点,转弯半径不小于1 km,障碍圆半径均为5 km。
仿真实验:设定复杂战场环境中有5 个威胁区已知,无人机初始点坐标(0,0),终点坐标(80,40),初、末运动方向角均为0°。分别对于经典PH 路径规划方法与本文提出的方法进行对比。实验结果如图4、图5 所示:
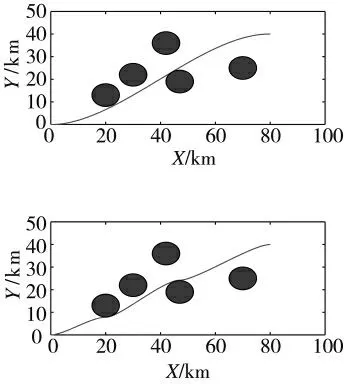
图4 经典PH 路径规划

图5 组合PH 路径规划

表1 算法结果对比
考虑到复杂战场中会出现突发障碍,在仿真环境中添加黑色障碍圆作为突发障碍,将重规划之后的结果进行对比。实验结果如图6、图7 所示:
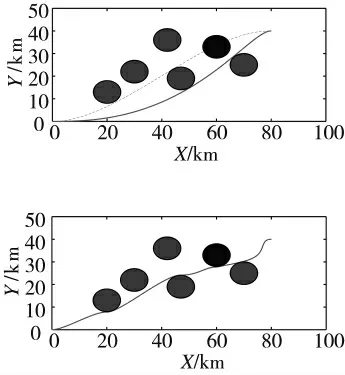
图6 经典PH 路径二次规划

图7 组合PH 路径二次规划
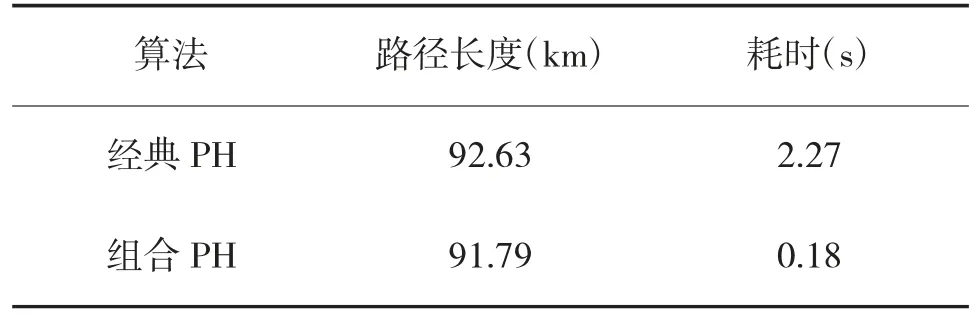
表2 二次规划算法结果对比
由仿真结果可知:在已知威胁战场环境中,采用经典PH 曲线方法进行航路规划,需要对所有障碍进行规避;采用智能算法调节参数过程长、计算量大、耗时长,而采用本文中提出的多段PH 路径组合方法,将每一段的PH 曲线构造过程大大简化,每一段至多考虑一个障碍,路径规划时长大大缩短。在算法对环境变化的动态响应方面,当环境中出现突发威胁,传统方法需要重新进行计算,规划全局路线,耗时较长;基于本文方法,出现突发障碍,仅需要将与该障碍相交的路线进行拆解,其余各段曲线不需要大幅度调整,航路规划时长大大缩短,具有很强的灵活性以应对复杂战场要求。
5 结论
本文提出了一种基于改进PH 曲线的无人机航路组合路径规划算法。利用PH 曲线平滑、曲率连续以及多项式特性,实现将多条单一PH 路径进行组合,结合贪心策略的快速寻优特性,能够快速高效地获取路径参数,以较少的时间代价、计算代价生成得到一条满足无人机运动学约束的全局路线。仿真验证表明本文提出的多路径组合规划方法,可以充分发挥PH 曲线的特性,规划效率和动态响应效果相对经典PH 算法有了很大提高。

