泛型直线螺线管型电磁阀运动分析和改进的电压控制

刘雨晨， 郁林聪2, 叶 骞

(1.上海交通大学 机械与动力工程学院， 上海 200240; 2.山西柴油机工业有限责任公司， 山西 大同 037036)

引言

直线螺线管型电磁阀是当前使用最广泛的电磁阀之一，具有结构简单、造价低廉、控制方便、工作频率高等优点。通常，由于这种螺线管电磁阀只具备开启和关闭2种工作模式而使得其只适用于作为流量开关使用。而近年来，由于电子技术的发展，使得高速性的开关电磁阀可以利用脉宽调制(PWM)的方式调节开关时间的比例(占空比)，来达到调节流量的效果，这使得这种廉价的高速开关型电磁阀逐渐代替昂贵的比例阀。

而现有的控制方法，主要使用方波信号对电磁阀占空比进行调整，这种方法的主要缺点在于控制的占空比不够精准，而且功率过高导致发热量大。有研究人员通过控制电流来控制电磁阀的动作[1]，这样的控制方法，在功率上有所降低，但不能充分的挖掘电磁阀的频率性能，使得其实际工作频率远小于其理论工作频率。

本研究采用阶梯型的两段电压以达到更精细地控制高速开关电磁阀。这样的控制，不仅能充分挖掘电磁阀的最大工作频率以及更精准的控制占空比，而且发热量更低。而要实现这一目标，必须先深入分析电磁阀的工作过程和衔铁运动的物理模型[2-4]。

1 直线型螺线管电磁阀衔铁的物理模型建立

图1为电磁阀衔铁运动时输入电压、位移、电流随时间变化关系图。在直线型螺线管电磁阀中，一般工作过程为：开启时，外界对电磁阀加载电压，电磁阀的线圈克服电感和电阻而产生电磁吸力，电磁吸力随着线圈电流增大而逐渐加强。直到电磁吸力大于弹簧预紧力，衔铁克服预紧力开始运动，经过一段时间后，衔铁达到开启状态。在关闭时，外界电压断开，线圈放电，当放到一定电流时候，电磁吸力小于弹簧预紧力，使得衔铁下落，直到闭合。所以要得到直线型螺线管衔铁的物理运动模型，先要分析静态下电磁吸力的计算[5-11]。

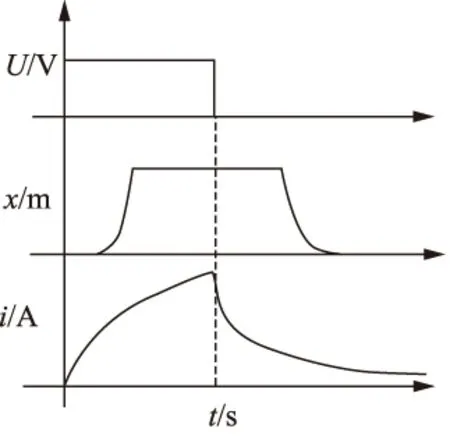
图1 电磁阀衔铁运动时输入电压、位移、电流随时间关系图

1.1 静态下电磁吸力的计算

对于任意磁体，在受到磁感应强度为B的作用下，其静态电磁力大小可以由Maxwell电磁力公式[12]得到：

(1)

式中,F—— 电磁力, N

S—— 电磁线穿过的作用面,m2

n0—— 法向量

μ0—— 空气磁导率,H/m

B—— 磁感应强度,T

对于如图2中的一般的直线性螺线管电磁阀，其电磁力的计算公式可以简化为[1]：

(2)

式中，Φ为总磁路中的磁通量,Wb。

1.阀座 2.衔铁 3.预紧弹簧 4.铁芯 5.线圈 6.铁芯固定件 7、8.密封圈

上公式的Φ,由下面方程组确定：

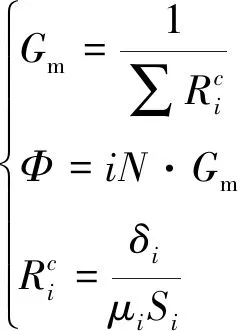
(3)

式中,iN—— 激励磁动势,Wb/H

Gm—— 磁路中磁导,H

δi—— 对应磁阻部分的间距,m

Si—— 对应磁阻部分的磁面积,m2

μi—— 第i部分的磁导率,H/m

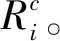
1.2 衔铁开始运动时间和电压的关系

要了解衔铁的运动过程，首先要知道衔铁在给定电压下的开始运动的时间。

在如图3所示的一般螺线管电磁阀的电路中，忽略电路连接电路的电感和电阻下，其输入电压和电流电感的关系式如下[1]：

(4)

式中，U—— 输入电压,V

i(t) —— 电路电流,A

L(x,t) —— 线圈产生的电感,H

R—— 线圈电阻,Ω

t—— 时间,s

x—— 衔铁位移量，当未通电时为0,m

图3 一般直线型螺线管电磁阀电路图

而螺线管的电感在有铁芯和空气间隙下随铁芯位移x的计算公式为[2]：

(5)

式中,d—— 螺线管的直径和长度,m

l—— 螺线管的长度,m

N—— 线圈匝数

μ—— 螺线管铁芯磁导率,H/m

x—— 衔铁位移量,m

x1—— 空气在磁路的长度,m

x0—— 铁芯在磁路中的长度,m

在衔铁上升运动前可以由式(5)知道电路的电感是不变的，所以在电磁阀电路中：

(6)

解得：

(7)

其中：

(8)

将方程式(7)联立方程组式(3)代入式(2)可以得到，电压和电磁力和时间的关系：

(9)

当吸力F等于弹簧预紧力F0时，其电流即为衔铁启动电流值。

对于在衔铁任意定值位移x下，时间趋于无穷时的理论电磁力F等于弹簧预紧力时即F为F0+Kx时，其输入电压为最小起励电压U0(x)，最小起励电压和时间关系如图4所示，由式(9)可以得到：

式中，U0(x) —— 输入电压,V

K—— 弹簧刚度,N/m

F0—— 弹簧预紧力,N

图4 最小起励电压和时间关系示意图

可以知道能使衔铁开始运动的最小理论电压U0(x)是关于位移x的函数。

同时由式(9)和式(10)可以知道，对于不同电压U(t0)，达到U0(x)的时间t0可以由下面式子得到：

(11)

式中,U(t0) —— 输入的电压,V

U0(x) —— 衔铁位移为x时的最小起励电压,V

R—— 线圈电阻,Ω

Ldown—— 在衔铁未启动时的线圈电感值,H

由上式可以知道，不同输入电压与电磁阀衔铁的开始运动时刻的关系如图1所示。可以知道，只要当输入的电压大于U0(x)|x=0，电磁阀就能吸合。并且从加载电压到衔铁运动响应时间可以由式(11)求解得到。

在知道衔铁开始运动的时间以及相关值后，就可以讨论衔铁的动力学模型了。

1.3 衔铁上升的动力学分析

衔铁的上升过程是指衔铁从刚开始运动，到运动完成，衔铁被吸住不动的过程，在此过程中不考虑衔铁的碰撞等因素。

在衔铁的上升运动中有：

(12)

式中,B—— 衔铁运动相关的阻尼系数,N·s/m

F—— 电磁吸力,N

F0—— 弹簧预紧力,N

K—— 弹簧刚度,N/m

m—— 衔铁的质量,kg

x—— 衔铁位移量，当衔铁开始运动时为0,m

t—— 运动时间，当衔铁开始运动时为0,s

为解得电流，位移和时间的关系，我们代入式(1)并联立式(4)就有方程组：

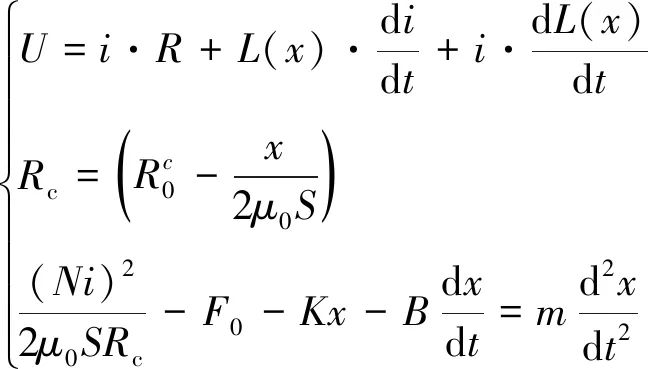
(13)

由式(10)对最小起励电压U0(x)有：

(14)

所以联立式(4)，式(13)和式(14)：

式中,i为线圈电流，初始值由式(9)可得。

求解方程组便可以得到上升运动过程电流随时间的关系，以及位移随时间的关系。这样便得到了上升运动结束后的电流和时间等信息。

1.4 衔铁上升运动结束后的情况分析

在衔铁上升运动结束后，只要当电磁阀吸力略微大于此时弹簧预紧力，电磁阀即可保持吸合状态。实际上，由于在电磁阀的衔铁的运动过程中，衔铁和铁芯的空气间隙不断减小，使得此过程实际上是整个磁路磁阻减小过程。而在此过程中，在输入电压不变下，线圈对衔铁的电磁吸力是越来越大的。所以在上升运动结束后，衔铁一定会吸合住。

在吸合的时刻，衔铁被吸住而静止。线圈继续充电，此过程有：

(16)

解得：

(17)

式中，Ltop—— 电路在衔铁被磁力吸合时的电感,H

i—— 电路电流，i0是当上升运动完成时的电流，可以由式(15)求解得到,A

t—— 时间，当上升运动完成时为0,s

当外界不在加载电压后，电路先进行放电，最终使得电磁吸力与弹簧预紧力等外力相等，这段过程有：

(18)

式中，i为电路电流，其初值为i1，即上述的充电过程结束时的电流值。

当电压为前面所提在吸合位置的最小起励电压U0(x)时电磁阀开始下落，并令此时U0(x)为Ufall。

在下落过程有：

(19)

联立式(4)并令输入电压U=0有方程组如下：

式中,i为线圈电流，初始值为i2,A。

解得上面微分方程组就可以得到下落过程的时间和结束后的电流。

2 电磁阀相关参数辨识的仿真实验

从前面的分析可以得到：要解得方程式(15)以及方程式(20)就必须要先求得L(x)和U0(x)的函数关系式。

在本研究先使用Maxwell仿真软件对模型进行参数辨识，模型对象为样本高速开关电磁阀，具体结构如图2所示，其中其衔铁的位移范围x∈[0, 0.2] mm，当上升运动未开始时位移为0，完全吸合时位移为0.2 mm。下面将阐述的参数辨识方法。虽然是以此样本阀为载体，但是方法使用于任意直线螺线管型电磁阀。

2.1 测量电感和最小起励电压的实验方法

测量的电感即是测量电磁阀电感随衔铁位移变化的关系如式(5)，而最小起励电压即为能使得衔铁运动的最小起励电压，其随衔铁位移变化的关系见式(10)。

其具体实验方法如下：

首先设衔铁位移量x=x0，在此条件下，调整输入电压，使得其在一定的范围取值，然后记录电压和衔铁从输入电压到衔铁启动的时间，并标记这组为x=x0的一组数据。所以接下来依次令x=x1，x=x2……以同样的步骤测得多组数据。

在本样本阀中对x分别取0, 50, 100, 150 μm，对于每个x取值，分别仿真得到输入电压U为25, 30, 35, 40, 45, 50, 60, 70, 80, 90, 100, 120, 140, 160, 180, 200, 250, 300 V一共90组仿真数据，数据包括电流随时间的关系，位移随时间的关系以及吸力随时间的关系。进一步处理可以得到衔铁启动的时间，即当位移不为0的时刻。

2.2 最小起励电压随位移的变化

对最小起励电压U0(x)，考虑一般电磁阀，其衔铁位移产生弹簧压缩力Kx远小于弹簧预紧力F0，所以式(10)可以简化为：

(21)

上式可写成：

U0(x)=ax+b

(22)

式中,a,b为线性参数。

再由式(11)可以知道，当衔铁位移一定时，输入电压U(t)和时间t的变化关系为：

(23)

所以可以用形似式(23)的函数，以及用前面仿真测得的x=0, 50, 100, 150 μm时，多组输入电压以及对应衔铁启动时间的值，即可拟合得到不同位移下的U0(x)值，再进而得到参数a,b的值。

2.3 电感随衔铁位移变化

由式(5)可以发现，电感在直线型螺线管内随衔铁位移变化是线性的，可以写为：

L(x)=αx+β

(24)

式中,α,β为线性参数。

并由式(11)和上式可以得到：

(25)

式中,U—— 控制的输入电压,V

t—— 外界加载电压到衔铁启动的时间,s

在式(25)中可以发现，对应每个不同的输入电压U和x都有唯一的衔铁启动时间t与之对应。所以由式(23)拟合得出指数系数ξ，即可进一步得到参数α和β。

2.4 参数辨识结果与微分方程求解以及仿真对比

此次仿真以图2所示电磁阀为样本阀，对上述步骤进行操作，得到的不同位移下，电压和衔铁启动时间及其拟合曲线如图5所示，确定的最小起励电压U0随位移的曲线如图6所示，以及电感随位移的变化如图7所示。

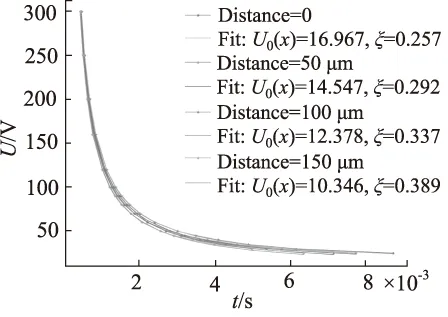
图5 激励电压随时间变化拟合曲线和仿真数据图

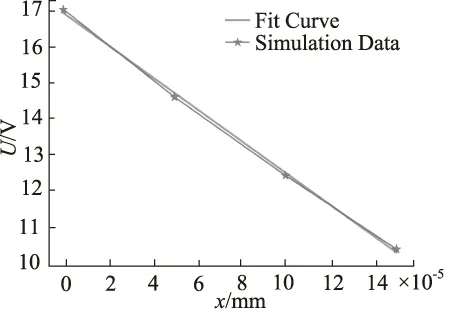
图6 最小起励电压随衔铁位移的变化

图7 线圈电感随衔铁位移的变化

在求得电感和最小起励电压后，就可以解出方程式(15)和式(20)。

由于方程式(15)和式(20)都是非线性微分方程组，很难找出方程的通解，这里先将方程组转化为状态方程组，然后采用Runge-Kutta公式[13]进行求解：对于上升运动过程。

由方程式(15)有：

(26)

式中,t—— 当衔铁开始运动时为0，衔铁上升运动结束后的时间为t1,s

R—— 线圈电阻，取35.4 Ω

i—— 电路电流，其初始电流值由式(9)可以计算得到,A

x—— 衔铁位移，未启动时为0,m

F0—— 弹簧预紧力，取15 N

K—— 弹簧刚度，取3000 N/m

m—— 衔铁质量，取0.0014 kg

B—— 衔铁阻尼值，取10 N·s/m

同时，在知道最小起励电压，以及在衔铁未运动时的电感情况下，衔铁从加载输入电压U到衔铁开始运动的时间t0可以由式(11)得到。

在限定衔铁最大位移x=0.2 mm的情况下，对于不同输入电压U的取值，其解得的线圈电流i随时间变化图8，衔铁位移x随时间变化如图9所示。

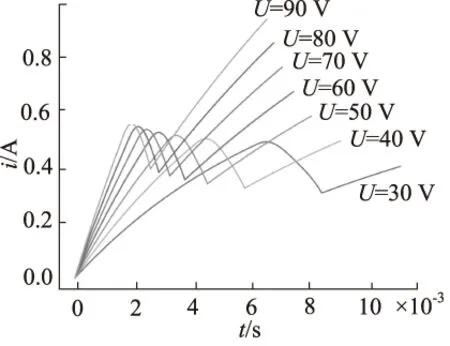
图8 上升过程线圈电流和时间关系图

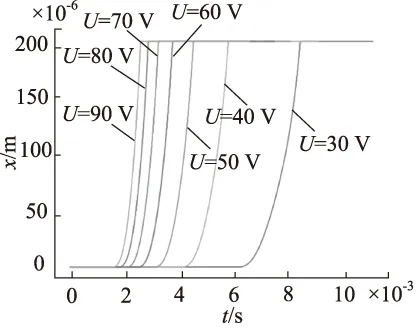
图9 上升过程衔铁位移和时间关系图

并将由上面方法计算得的衔铁启动时间t0并加上上升结束时间t1与仿真结果对比，如表1。从表中可以发现，求解的时间和仿真时间的误差均小于5%，说明理论模型的正确性。

2) 对于下落过程

对于方程式(20)有：

(27)

式中,t—— 衔铁下落的时间，在开始下落时为0,s

i—— 线圈电流，在知道最小起励电压值后，其初始值i2的由式(20)可以得到,A

表1 微分方程理论解和仿真解对比

在最小起励电压确定后，其下落过程的解唯一，其线圈电流随时间的变化如图10所示，衔铁位移随时间的变化如图11所示。

图10 下落过程线圈电流和时间关系图

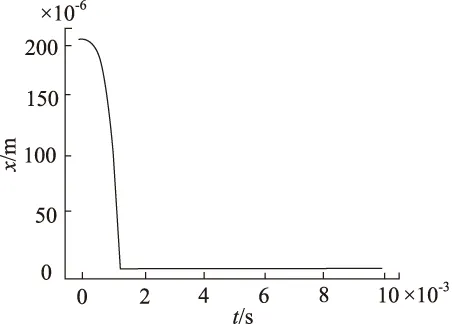
图11 下落过程衔铁位移和时间关系图

3 基于两段阶梯电压下的电压控制策略

通过直线螺线管电磁阀衔铁的电路分析和动力学分析，发现可以通过使用高电压和低电压组合的两段阶梯电压的控制方式能有效提高电磁阀的实际控制频率和精准地控制占空比，同时也能减小电磁阀功率。

3.1 两段阶梯型电压控制策略

此策略是使用两段不同电压值Uhigher以及Ulower来控制电磁阀，其中这种控制方式满足：

(1) 控制的高电压在上升运动结束前为Uhigher，这时衔铁刚好完全吸合，此时电流为i1；

(2) 可以使得控制低电压Ulower降到衔铁被磁力吸合时最小起励电压U0(x)，并保持一定时间，以满足给定占空比要求。这样可以一直保持吸合状态，在此过程结束时的电流为i2；

(3) 再输入电压为0，此时由于上面阶段选择的控制电压Ulower=U0(x)，此段过程会经历3个阶段：一是线圈继续放电，直到线圈电压小于此位置的最小起励电压U0(x)。二是衔铁开始下落，直到下落结束。三是下落结束放电直到此周期结束。

所以在此种控制方案下，整个过程如图12所示：开始加载高电压Uhigher，时间为0→衔铁开始上升运动t0→衔铁完全吸合t1→控制电压为Ulower，保持时间为t2→线圈放电直至衔铁开始下落t3→衔铁下落过程结束完全关闭t4→电路继续放电到此周期结束t5。

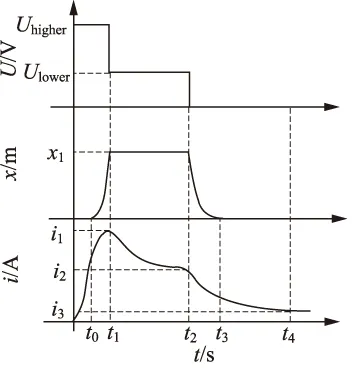
图12 新控制策略的输入电压、位移、电流随时间变化过程

3.2 梯形电压控制策略的仿真实验

分析了衔铁运动的各个过程，得出了基于理论过程分析的控制策略，并通过仿真实验进而计算得到了衔铁的各种参数。这样就可以利用前面的结论应用于实际控制中。在此，采用仿真的方式验证控制策略的有效性。

在前面的参数辨识和微分方程的计算后，确定了衔铁启动的时间t0，衔铁运动过程的时长t1以及吸合后的最小起励电压U0(x)，可以依据上述方案设计控制高低电压Uhigher和Ulower，在考虑到一定的理论计算误差下，采用策略对电磁阀进行控制如下：

以图4的样本电磁阀进行仿真实验，设置两组仿真进行实验：

第一组作为对比，以常规PWM方波控制方法进行控制，设置其电压为24 V，占空比为50%的方波进行控制，方波的频率为50 Hz。

而以新控制策略方法设置第二组。其中选用Uhigher=55 V，由上述方法解得其衔铁启动时间t0=2.6646 ms，上升运动时间t1=1.3966 ms考虑到误差，取高电压的持续时间为thigh= 105%·(t0+t1)=4.2643 ms，并由前面参数确定最小起励电压U0(x)在吸合位置电压为7.358 V，考虑到控制的冗余，取低电压Ulower=8 V。

两者的仿真结果如图13所示，从中可以发现，使用传统PWM控制的电磁阀的衔铁在刚开始加载时，并不能正常工作。而在之后的运动中，尽管控制的占空比为50%，但实际仿真的占空比远小于50%。说明电磁阀在50 Hz频率下，用传统方法已经不能准确控制阀的开关时间了。

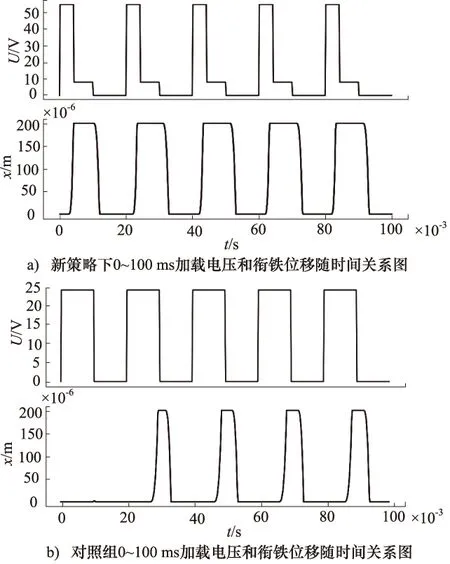
图13 样本阀以新控制策略以及传统控制的输入电压和位移随时间关系图

而使用新控制策略方法进行控制，可以发现。同一电磁阀的衔铁不仅在加载开始时能正常运作，而且控制所要求的占空比也能很好的满足其要求。

从上面的仿真结果能有效的证明了本研究两段阶梯电压控制策略方法能更精准的控制电磁阀的占空比，同时如果设置低电压Ulower为0也能得出电磁阀频率提高的结论。

4 结论

本研究从电磁阀衔铁的静态吸力出发，由电磁吸力公式得出了主要影响电磁阀工作性能为电压的结论。然后通过分析电磁阀衔铁的运动过程，得到了各个阶段的时间、电流的计算方程。同时要解出计算方程，设计并实验得到了计算方程中的相关参数并进行了仿真验证。在得到电磁阀相关计算方法的参数后，由运动过程，发现了使用两段阶梯电压控制电磁阀的新的控制方法。然后将新的控制方法并结合得到的参数，应用于仿真中，经过与传统PWM控制方式作对比，得出了新的控制方法的有效性，进而间接验证了推导的正确。