微型高压压缩机效率的数值分析

(华中科技大学 数字制造装备与技术国家重点实验室， 湖北 武汉 430074)

引言

高压气体在石油、化工、船舶、军事、救援、食品等领域有着广泛的应用，主要用于冷却、潜水呼吸、气动弹射、天然气系统等[1]。目前用于输出高压气体的压缩机的主要特征为体积大、重量重以及有油润滑，对体积重量要求严格的移动设备无法应用；同时，无法适应高功率密度比、适应大温差范围、免后期维护等特殊工况的要求。将微型高压压缩机应用于航空航天、海洋以及天然气等领域具有响应快、效率高等显著的优势[2]。

热力性能参数是评价压缩机的重要指标，包括容积流量、排气压力、排气温度以及功率和效率等[3-4]。SUN，FARZANEH-GORD等[5-7]采用数值解析与试验的方法研究了传统往复式压缩机的热力学特性，并揭示了其关键影响参数。CASTAING，PEREIRA等[8-10]通过CFD方法对传统往复压缩机的工作过程进行三维建模并分析了气阀、活塞速度与热力学特性的相互影响关系。

微型高压压缩机的体积小且排气压力高，需采用紧凑的多级压缩结构，各级气缸内的压力特征区别明显，其热力学及效率特征存在较大差异。此外， 结构与压力的差异，也会导致影响各级效率的敏感参数不尽相同， 因而建立起微型高压压缩机内各级效率评估的数值模型是十分必要的。

本研究提出了一种无油润滑的微型高压压缩机。根据微型高压压缩机的关键指标，确定微型高压斜盘压缩机的关键结构参数，在此基础上，建立气缸压力变化的仿真模型，对压缩机的工作过程进行数值模拟，研究主轴转速对气缸压力变化和进气量的影响，进而分析其对容积效率、等熵效率的影响。

1 微型高压压缩机结构及工作原理

斜盘式压缩机具有结构紧凑、噪声低以及稳定性好等优势，将其多级活塞同圆周平行布置于气缸内，从而将单级多活塞的斜盘式压缩机改进为多级斜盘式压缩机，以满足微型高压压缩机的压力、排气量、体积以及重量等关键技术要求。

根据表1的关键指标，结合多级压缩原理和多级斜盘压缩机的结构特征，求得微型高压压缩机的各级参数，如表2所示。由表2可知，压缩机采用四级压缩结构，最大缸径为44 mm，最小缸径为5 mm，第四级的压力范围最高，最高输出压力为41 MPa。在回冷不完善度为0 ℃的情况下，各级的温度变化均一致，当回冷不完善时，下一级的吸气温度会比上一级的吸气温度高，因而需要通过良好的级间冷却保证各级输出高温气体的高效冷却。

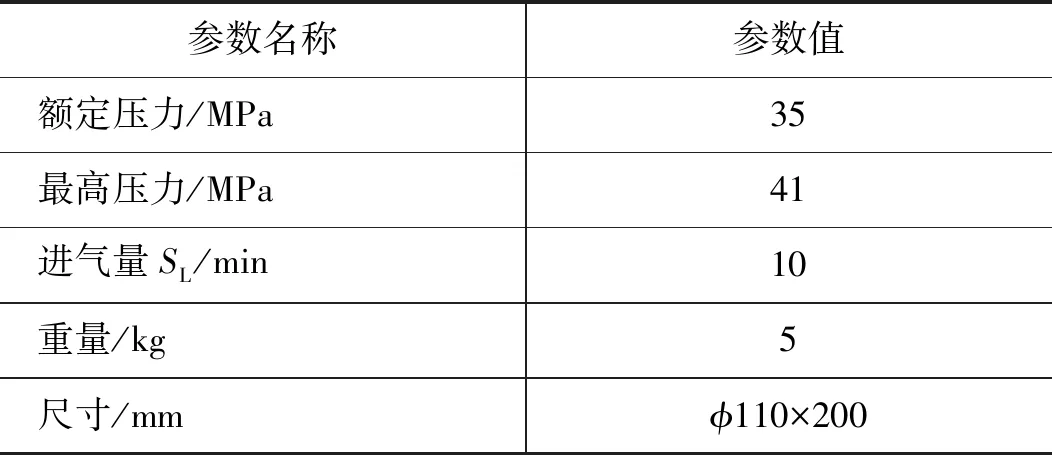
表1 微型高压压缩机关键指标

表2 压缩机各级参数

微型高压压缩机的结构模型(仅显示两级压缩结构)，如图1所示，包括主轴、斜盘、滑靴、缸体、多级活塞、进气阀、排气阀。

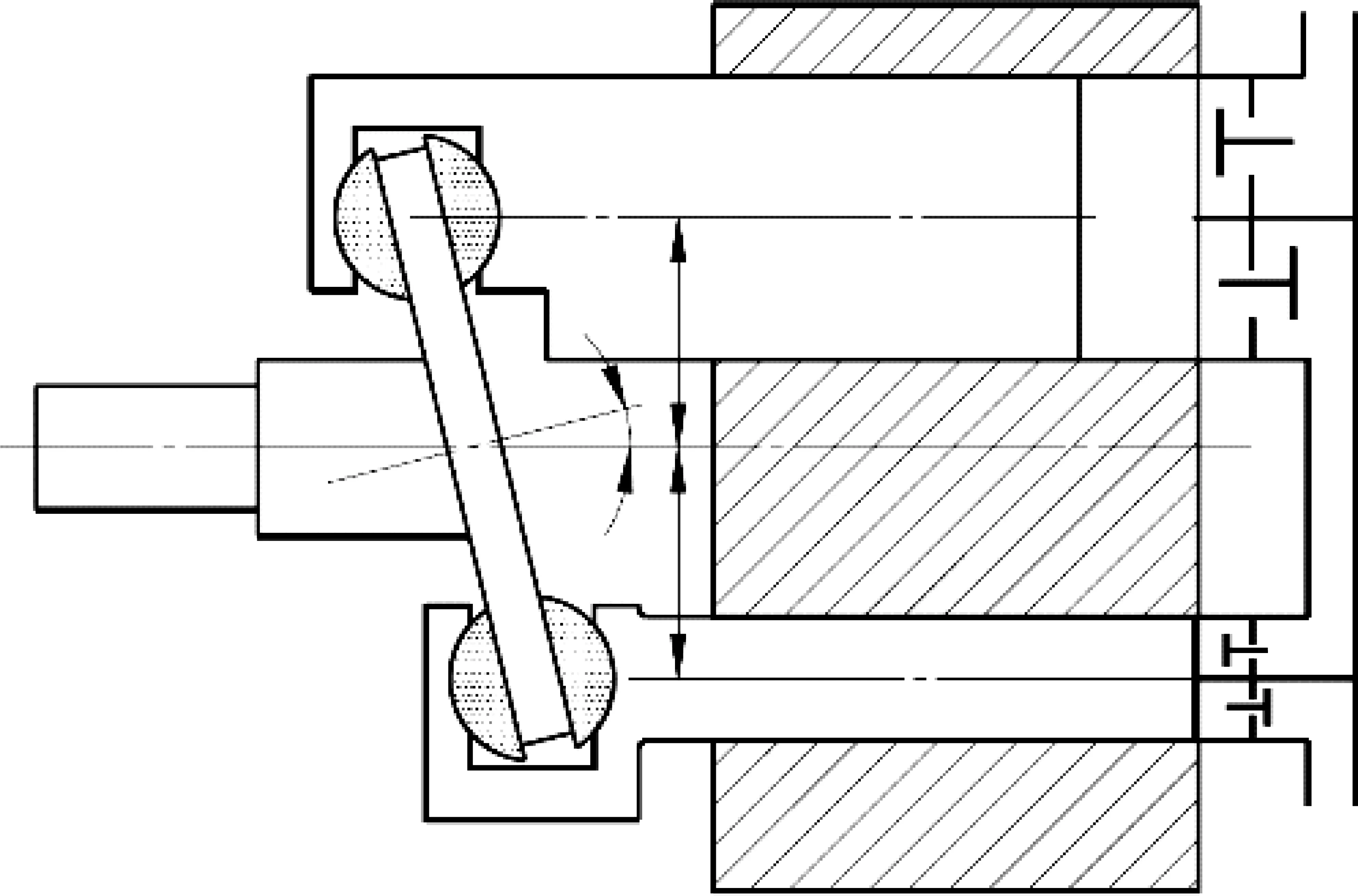
图1 微型高压压缩机结构原理图

主轴的旋转运动通过斜盘及滑靴转换成多级活塞的直线往复运动，每一级活塞均配有吸气阀和排气阀，活塞的往复运动协同吸气阀和排气阀的动作，实现气体的多级压缩。

2 压缩机工作腔热力过程建模

压缩机工作腔热力过程模拟，是以压缩机实际循环中的4个工作过程(膨胀、吸气、压缩、排气)为研究对象，综合考虑影响它们的各种因素，建立起物理数学模型，并在计算机求解。这样不仅能够得出压缩机的宏观特性—流量和功率，也能得出压缩机的主要热力参数(p、T、V)随转角(时间)变化的瞬态特性[11-15]。

2.1 能量守恒方程

忽略工作腔的泄漏，能量守恒方程可由式(1)表示：

(1)

其中，d(mcuc)为dθ转角内气缸工作容积内气体的热力学增量； dQ为dθ转角内工作容积壁面与气体间传递的热量； dmi， dmo为dθ转角内通过进气阀和排气阀的气体质量；hi，ho为通过进气阀和排气阀气体的比焓； dW为dθ转角内活塞对气体做功增量，其表达式为。

dW=-pcdVc

(2)

式中，pc为气缸内压力；Vc为气缸工作容积。

2.2 质量守恒方程

根据变质量热力系统质量守恒方程，可得到工作腔质量连续方程如下所示：

(3)

式中， dmc为dθ转角内气缸工作腔内气体质量的增量，通过进气阀、排气阀的气体质量变化可用式(4)表示。

(4)

其中，Cdi，Cdo为进、排气阀阀口流量系数；Ai,Ao为进、排气阀阀隙有效通流面积。ρi,ρo为进、排气体密度;ω为角速度； sign为符号函数。

2.3 气阀运动方程

以环状阀为例，将气阀阀片的运动简化为单自由度，得到进气阀和排气阀的运动微分方程如式(5)所示[16-17]。

(5)

其中，yi，yo分别表示进、排气阀片的位移；Mi，Mo分别表示进、排气阀片等效质量；βi，βo为进、排气阀阀口推力系数；Zi，Zo为同类气阀的个数；ki，ko表示弹簧刚度；yi0，yo0表示弹簧预压缩量。

(6)

其中，Cr为反弹系数，脚标imp表示冲击值，reb表示反弹值。

2.4 活塞运动方程

微型高压压缩机采用如图1所示斜盘结构，得到活塞运动方式如式(7)所示[18]。

S(θ)=R(1-cosθ)tanγ

(7)

式中，R，γ分别表示缸体分布圆半径以及斜盘倾角。在此基础上得到工作腔容积变化公式如式(8)所示。

Vc(θ)=Ac×S(θ)+V0

(8)

2.5 气体状态方程

本研究利用实际气体的状态方程式来描述气体压力、温度和密度之间的关系。实际气体的状态方程有很多种，比如范德瓦耳斯气体状态方程、雷特里奇—匡(Rcdlich-Kwong)气体状态方程等。本研究主要采用了雷特里奇—匡(Rcdlich-Kwong)方程，其实际气体的状态方程的公式为：

(9)

式中，a、b是被压缩气体的相关常数，其计算方法如下：

本研究将空气作为研究对象，空气的临界状态的相关参数为：Tcr=132.5 K，pcr=3.77 MPa，普适气体常数为R=8.314 J/(mol·K)。

2.6 效率计算

压缩指示功率、容积效率和等熵效率将用于评估实际压缩过程的合理性，分别如下所示。

压缩指示功率由下式表示：

(10)

转换成式(11)，如下所示。

(11)

容积效率可由下式表示:

(12)

等熵效率可由下式表示:

3 仿真结果分析

采用四阶龙格-库塔法对上述方程组进行联立求解，并进行后处理计算。将主轴转速分别设置为600, 800, 1000, 1200 r/min，得到结果如下所示。

3.1 工作腔压力

各级工作腔压力随转速的变化如图2～图5所示。由图可知，转速主要影响工作腔的压缩及排气过程，尤其对排气过程的影响较为显著，而对膨胀、吸气过程的影响不明显。当转速为600 r/min时，排气过程较为平稳，前三级的压缩峰值压力为0.56， 2.25, 9.50 MPa。随着转速的升高，排气过程的压力脉动变得更加剧烈，转速为1200 r/min时，前三级的最高压力分别达到了0.58， 2.34， 10.20 MPa，同时，第一级的排气过程出现了低于正常排气压力值的现象，最低压力值为0.43 MPa。

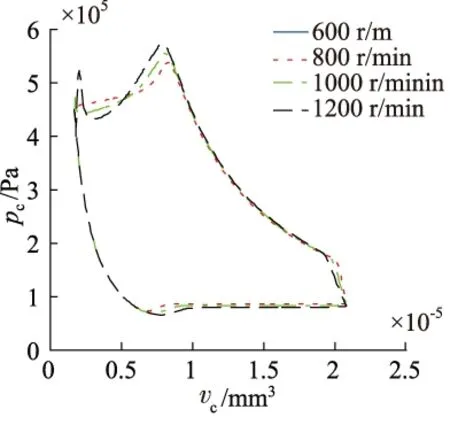
图2 一级工作腔压力变化曲线

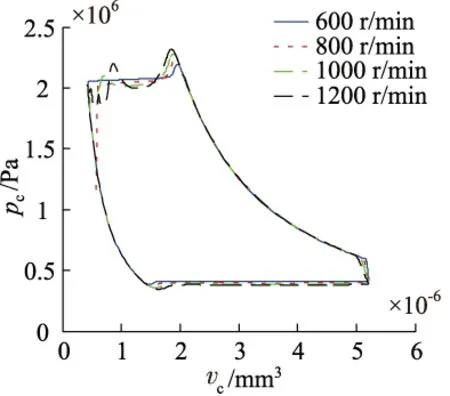
图3 二级工作腔压力变化曲线

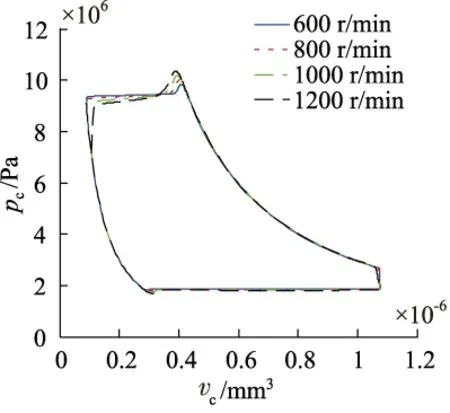
图4 三级工作腔压力变化曲线

图5 四级工作腔压力变化曲线

此外，通过计算发现，转速为600 r/min时，第四级工作过程压力曲线出现异常，同时，第四级的气阀出现了开启和关闭的异常，因而600 r/min的工况未在文中体现。该现象表明第四级气阀的参数已无法匹配，导致第四级工作腔内部气体的膨胀、吸气、压缩以及排气出现异常。为此，需要根据运行转速对各级的气阀进行优化匹配。

3.2 工作腔气体质量

各级工作腔内气体质量变化曲线如图6～图9所示，在一个工作周期内，随着转速的提高，第一级和第二级的工作腔气体质量变化趋势较为明显，在吸气阶段，同一转角的情况下，低转速时工作腔气体质量高于高转速时，这表明进气阀开启时间随转速的提高而延后。从图8和图9可知，对于第三级和第四级，不同转速下的气体质量变化曲线基本重合，这表明，转速对这两级工作腔的气阀开启和关闭基本无影响。

图6 一级工作腔气体质量变化图

我们可以发现，转速对最终的进气气体质量也存在影响，对于第一级，转速从600 r/min提高至1200 r/min时，一个周期内进气质量从 2.85×10-5kg增加至2.91×10-5kg；对于第二级和第三级，600 r/min时，一个周期内进气质量分别为2.66×10-5kg和2.50×10-5kg，当转速提高至1200×10-5kg时，进气质量分别为2.64×10-5kg和2.50×10-5kg。对于第四级，转速为800， 1000， 1200 r/min时，进气质量分别为2.61×10-5， 2.62×10-5， 2.61×10-5kg。因而可以发现，转速对后三级的进气质量影响程度比第一级稍小。

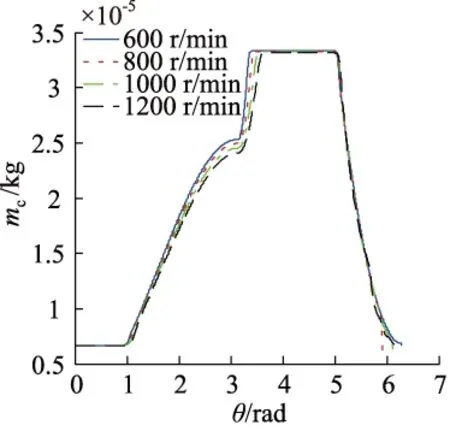
图7 二级工作腔气体质量变化图

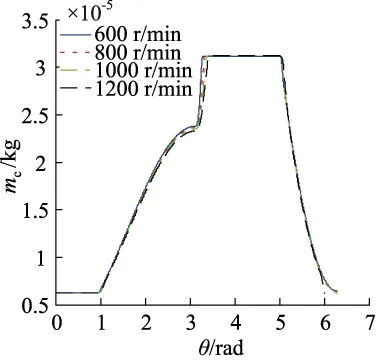
图8 三级工作腔气体质量变化图

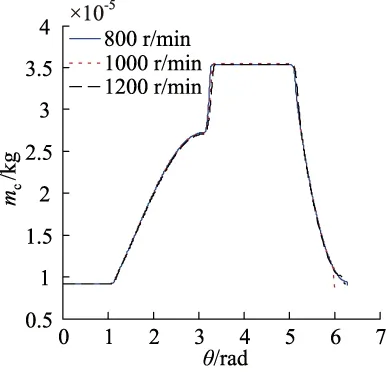
图9 四级工作腔气体质量变化图

3.3 容积效率

在上述对微型高压压缩机的各级工作腔气体质量变化的分析的基础上，进一步对各级工作腔的理论容积效率进行计算，如图10所示。由图10可知，第一级的容积效率较低，600 r/min时为62.1%，提高转速至1200 r/min，容积效率升至63.3%，这是由于第一级工作腔的吸气压力低，影响气体的吸入；对于第二级，吸气压力上升，因而容积效率上升，达到84%；此外，从图10可以看出，第三级和第四级具有超过95%的容积效率，第三级的甚至超过了99%，这表明该两级工作腔具有较好的气阀匹配特性。

图10 各级容积效率对比

3.4 等熵效率

等熵效率常用来评价工作腔内一个工作循环的完善程度[6]。从图11中的各级等熵效率对比可以看出，后三级工作过程具有较好的完善度，等熵效率均超过90%，第四级的效率最高，在800 r/min至1200 r/min的达到了95%，第一级的等熵效率随着转速的提高呈现下降的趋势，这是由于工作腔压力变化更为剧烈，与理想的工作过程曲线的符合度降低，从而导致等熵效率的下降。

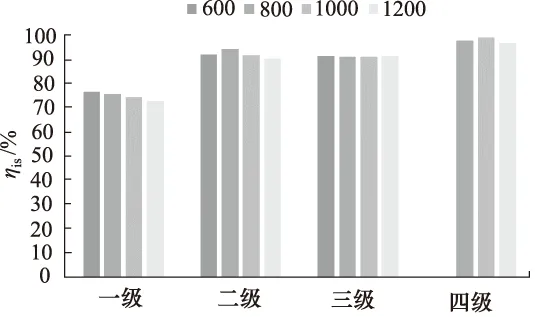
图11 各级等熵效率对比

4 结论

通过对微型高压压缩机进行热力学建模，对不同转速下高压压缩机各级工作腔压力、气体质量进行了分析，在此基础上，研究了各级工作腔的容积效率以及等熵效率与转速之间的关系。研究发现，转速的提高将增加排气过程的压力脉动，并在一定程度上降低工作腔的等熵效率；转速对前两级进气质量的影响较为显著；相较于后三级工作腔，第一级的容积效率较低。本研究将为不同工况下微型高压压缩机的参数优化匹配提供参考价值，进而为提高微型高压压缩机的效率提供依据。