同步阀原理性误差分析与全补偿理论的建立
蒋 淋, 姚平喜
(1.太原理工大学 机械工程学院, 山西 太原 030024; 2.精密加工山西省重点实验室, 山西 太原 030024)
引言
液压系统中经常会有两个或多个液压执行元件需要实现同步运动的情况[1]。实现液压同步的方案有很多,可归纳为开环控制系统和闭环控制系统。其中开环控制中没有压力反馈补偿环节,其同步精度取决于液压控制元件本身的制造精度和负载刚度;闭环控制中有对液压执行元件偏差信号的检测和负反馈环节,相对同步精度高,但是其结构较开环系统复杂,且制造、使用、维护和保证其较高的可靠性难度大[2]。因此,在很多情况下,开环控制仍然是液压同步技术中的首选方案,尤其是同步阀因其价格低廉、性能稳定的优点得到了广泛的应用[3]。
目前市场上普遍使用的同步阀具有两级结构,第一级结构是2个固定节流口,它的主要作用是将流量信号转化成压力信号反馈给左右弹簧腔;第二级结构是2个可变节流口,它主要作用是对负载压差进行补偿,其过流面积大小受阀芯两端压力反馈控制[4]。在实际工作中,同步阀经常会出现负载压差和入口流量不等于额定流量的情况,从而产生同步误差,这些误差是原理性的,不会因同步阀加工精度的提高而减小。
不能适应较大范围的偏载和流量波动大大限制了同步阀的实际应用范围[5],为此国内外学者从以下3个方面做了研究:改变一次节流口,比如可调式同步阀和自调式同步阀,但是它们都不能适应流量经常变化的场合[6];研究影响同步阀精度的因素(液动力、内漏、簧的不对称力、制造误差等)对结构进行改进或者对结构参数进行优化[7];将同步阀与其他元件一起组成同步回路,它的特点是不完全依赖同步阀来控制系统同步,相对系统复杂,成本高,响应时间长[8]。
由负载压差和流量变引起的同步误差是原理性的,不会因为阀制造精度的提高而减小,除此之外,偏载和流量波动造成同步阀产生同步误差的机理不同,很难用一种统一的方法去补偿,因此提出对其分别进行补偿的方法来实现对原理性的同步误差的全补偿,即为原理性误差全补偿理论。基于该理论提出一种具有三级结构的新型同步阀模型,第一级结构为固定节流口,第二级结构为负载压差补偿级,第三级结构为流量偏差补偿级,后两级结构按照同步误差随负载偏差和流量波动的变化规律进行设计。
1 同步阀误差分析
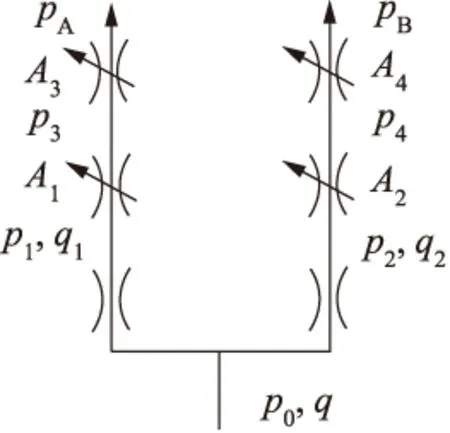
传统同步阀由2个固定节流口和2个可变节流口组成,如图1所示。2个固定节流口的面积和入口压力相同,要保证两支路流量q1=q2,只需保证两固定节流口出口压力p1=p2即可[9]。根据薄壁小孔流量公式:
(1)
式中,q—— 入口流量
Cd—— 节流口流量系数
A0—— 薄壁小孔横截面积
Δp—— 薄壁小孔两端压力差
ρ—— 液压油密度
则通过两可变节流口的流量q1,q2分别为:
(2)
(3)
式中,A1,A2—— 可变节流口面积
p1,p2—— 可变节流口入口压力
pA,pB—— 负载压力
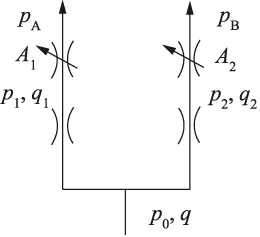
图1 传统同步阀原理图
在负载压差不为0且入口流量恒定的情况下,此时两支路负载pA≠pB,由于流体内分子之间的挤压必然使两固定节流口出口压力p1≠p2,从而导致两支路流量q1≠q2[10]。根据式(2)和式(3),要消除负载压差引起的同步误差,只需使可变节流口面积满足:
(4)
当负载压差为0时,入口流量的变化不会引起同步误差。当负载压差不为0时,阀芯在负载压差的作用下,处于某固定位置,2个可变节流口位置固定且其面积大小A1与A2满足式(4)。此时若入口流量发生变化,必然导致式(4)建立的平衡被打破,从而导致q1≠q2,此时的同步误差是由流量偏差引起的。
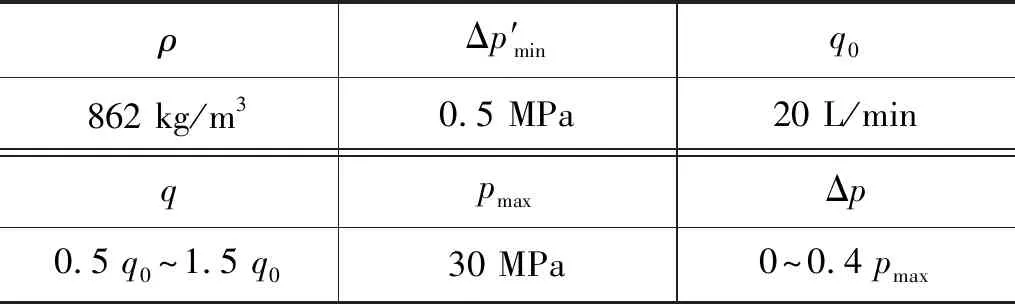
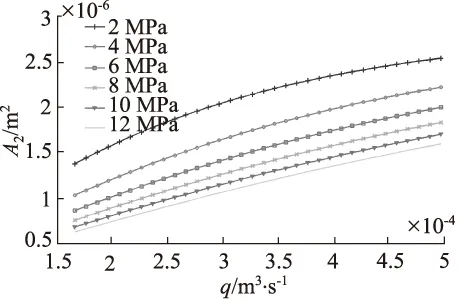
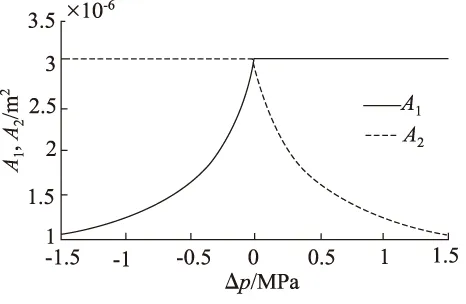
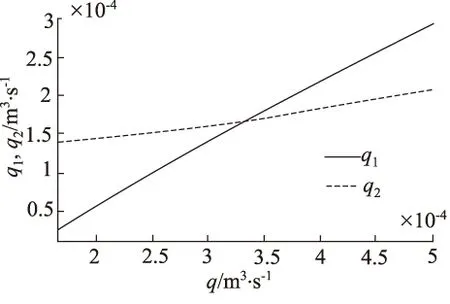
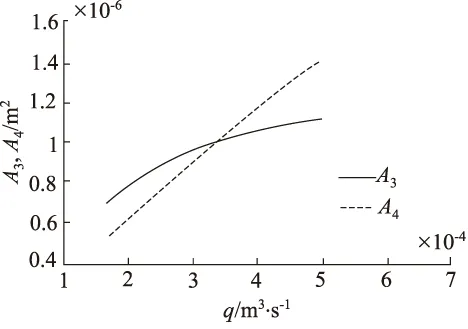
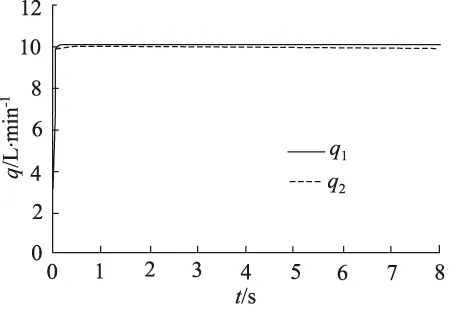
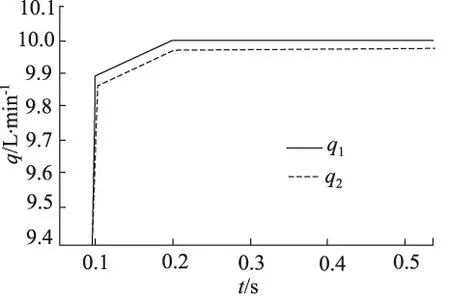
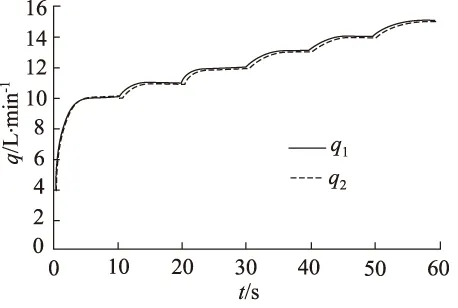
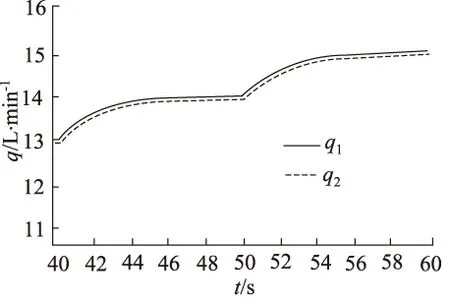
由式(4)可知,为使两支路流量相等,当pA>pB时,要增大A1,减小A2;当pA 为了解决这些问题,提出负载压差补偿级的设计采用单边补偿的方式,即产生负载压差时,把负载小的一端开口减小,负载大的一端开口不变,最终使两支路液阻相等,实现流量的平均分配。假设两支路负载pA>pB,导致两支路流量q1 (5) (6) (7) 根据同步阀的应用选取其额定流量q0和最大负载压力pmax,使入口流量可在额定流量50%的范围内变化,负载压差在最大负载压力40%的范围内变化。用MATLAB画出节流口面积随入口流量和负载压差变化的曲面,如图2所示,其中仿真参数如表1所示。从图中可以看出负载压差越大节流口面积越小,入口流量越大节流口面积越大,且变化规律都是非线性的。 图2 节流口面积随流量和负载压差的变化 表1 MATLAB仿真参数表 为了研究仅有负载变化时,可变节流口面积的变化趋势,用MATLAB根据式(7)画出在不同的恒定入口流量下节流口面积随负载压差变化的曲线,如图3所示。从图3中可以看出,负载压差越大,节流口面积越小且负载压差每增大2 MPa,节流口面积减小的幅值越小,呈现出典型的非线性关系,该节流口面积变化曲线是容易实现的。 同理,为了研究仅有入口流量变化时,可变节流口面积的变化趋势,根据式(7)用MATLAB画出在不同的负载压差下节流口面积随入口流量变化的曲线,如图4所示,从图4中可以看出入口流量越大,节流口面积越大且入口流量每增大5 L/min,节流口面积增大的幅值没有明显变化,入口流量变化对可变节流口面积的影响近似为线性,因此通过可变节流口面积变化能对入口流量变化产生的同步误差起到较好的补偿。 图3 不同流量下节流口面积随负载压差的变化 图4 不同负载压差下节流口面积随流量的变化 传统同步阀可变节流口的面积是是关于阀芯位移的二元函数,如图2所示,所以通过一组可变节流口的面积变化是无法同时消除负载压差和流量偏差所造成的同步误差的。通过分析从图3和图4发现,利用两组可变节流口对负载压差和流量偏差引起的同步误差分别进行补偿是能够实现的。 对由负载压差和流量偏差引起的同步误差分别进行补偿,并通过它们影响可变节流口面积的变化规律尽量进行完全补偿,即为原理性误差全补偿的理念,基于此提出具有三级结构的新型同步阀模型,如图第一级为固定节流口,第二级为负载压差补偿级,第三级为流量偏差补偿级,如图5所示。 图5 新型三级同步阀原理图 第一级固定节流口的作用将流量信号转换为压差信号反馈给阀芯两端,还能防止系统启动关停或者换向时同步阀中出现液压冲击。减小固定节流口直径会减小流量差从而提高阀同步精度,所以将2个固定节流口设计为细长孔,细长孔的流量公式为: (8) 式中,d—— 固定节流口直径 l—— 固定节流口长度 η—— 液体动力黏度 Δp′ —— 通过固定节流孔的前后压差 根据原理性误差全补偿理论,我们假设入口流量为额定流量,即q=q0,此时偏载产生的误差通过负载压差补偿级对其进行补偿。根据前文提到的单边补偿,我们假定两支路负载压差Δp>0,此时左可变节流口面积A1为常数,代入式(7)得到右可变节流口面积A2的关于负载压差Δp的函数: (9) 同理,当Δp≤0时,A2为常数,代入式(7)得到左可变节流口面积A1的函数: (10) 用MATLAB画出两节流口面积随负载压差变化的曲线,如图6所示,当Δp>0时,Δp越大,A2越小,其斜率越小;当Δp<0时,Δp越小,A1越小,其斜率越小;当Δp=0时,A1=A2。负载压差补偿级可变节流口面积随负载压差的变化趋势符合根据图3得出的结论。 图6 节流口面积随负载压差的变化 若入口流量改变,用流量偏差补偿级对流量偏差进行补偿,可变节流口变化的最终结果要使两支路液阻相等,根据流量关系q=q1+q2,联立式(2)、式(3)、式(8),得到q1关于q的函数: (11) 用MATLAB画出q1,q2随q变化的曲线,如图7所示,q越大,q1,q2越大,且q1的变化幅度大于q2的变化幅度,两条曲线的交点为(q0,A0)。根据图7得出结论,当q 图7 两支路流量随入口流量的变化 假设入口流量从额定流量q0变成了q,为了使两支路液阻相等,负载压差补偿级的压差变化和流量补偿级的压差变化总值要相等,即Δ(p3-pA)=Δ(p2-p4)+c,将薄壁小孔流量公式代入有: (12) 同理Δ(p4-pB)=Δ(p1-p3)+c,即: (13) 式中,A3,A4—— 流量偏差补偿级左、右可变节流口面积 c—— 常数 式(12) 、式(13)变形得到两可变节流口面积函数: (14) (15) 公式变形过程中常数c变成了c′,当c′=0时,用MATLAB画出流量偏差补偿级两节流口面积随入口流量变化的曲线,如图8所示,q 图8 节流口面积随入口流量的变化 结合新型同步阀工作原理,利用AMESim对软件其进行仿真。新型同步阀在入口流量为额定流量20 L/min、负载压差在最大负载压力40%的范围内,即0~12 MPa内变化时,左、右两支路流量q1,q2随时间变化如图9所示。图10为在不同负载压差下q1,q2的局部放大图,根据同步误差的计算公式 得出,当负载压差为0时,同步误差最小,其值为0.3%;随着负载压差增大,同步误差缓慢增加,维持在0.4%左右。 图9 不同负载压差下q1, q2随时间的变化 图10 不同负载下q1, q2局部放大图 在负载压差为10 MPa、入口流量在在额定值50%的范围内,即20~30 L/min变化时,左、右两支路流量q1,q2随时间变化如图11所示。图12为局部放大图。通过同步误差的计算公式,得到不同入口流量下同步阀对应的同步误差,在入口流量为额定值20 L/min 时,同步误差为0;随着入口流,量增大,同步误差略微上升,在入口流量为20 L/min时,同步误差达到最大值0.6%。 图11 不同流量下q1, q2随时间的变化图 图12 不同流量下q1, q2局部放大图 (1) 针对同步阀分流精度低的现状,对同步阀产生误差的原因进行了分析,得到了欲使分流误差为0时可变节流口开口面积的变化规律,为实现误差的全补偿提供了依据; (2) 针对负载偏差引起的误差和流量偏差引起的误差的不同变化规律,提出对负载偏差引起的误差和流量偏差引起的误差分别补偿的原理,并按照变化规律尽量进行完全补偿,即原理性误差全补偿的概念。提出三级阀的概念,第一级为固定节流口,第二级为负载压差补偿级,第三级为流量偏差补偿级,对由负载偏差和流量偏差引起的误差分别完全补偿,并分析了负载偏差补偿级和流量偏差补偿级的节流口面积的变化规律; (3) 提出一种高精度(同步误差低于1%)、抗负载压差能力强(为最大负载的40%)、抗流量偏差能力强(为额定流量的50%)的新型同步阀模型。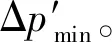


2 原理性误差全补偿理论
3 仿真验证
4 结论

