数学课本习题在高三复习中的价值再发掘

李 昌

一、引言

在高三复习教学中，不少教师青睐课外习题，特别信奉高考模拟题、名校考题，轻视课本习题（本文指苏教版高中数学教材上的“练习”“习题”和“复习题”）。他们认为课本习题太基础，难度不能直接达到高考要求，加之在新授课时已经做过讲过，没必要“炒剩饭”。这种意识不仅将学生引向了课外习题组成的题海中，而且也削弱了课本中习题的作用。课本习题对于高三复习教学是否还有价值，或者说课本习题的教学价值在新授课时是否发挥殆尽呢？为此，有必要对课本习题的教学价值与功能加以分析。

二、课本习题的价值分析

课本习题有重要的教学功能，它是教材的有机组成部分，是经过编者精心挑选的。新授课的教学多以知识理解为教学目的，那时课本习题一般以“模仿性习题”的形式出现，主要起巩固知识、评价教学即时效果的作用。由此可见，彼时的课本习题发挥的只是显性的练习功能，其隐性的教育功能、发展功能等还没有得以发挥。

此外，课本习题功能的发挥受多种因素的影响。因为习题的功能发挥程度会受到课型、教学环节等客观因素的影响。例如同一题目在新授课、习题课、复习课、试卷讲评课、作业环节、测验环节的教学功能和价值是不一样的。另外，习题功能发挥过程是动态和生成的，会受到教学情境的影响。例如同一个教师在不同的教学节点、不同认知水平的教学班级用同样的教学方法教授同样的题目，其教学效果绝不相同，题目的教学功能和价值也就大相径庭。

由此可见，即便是高考真题、名校考题，若没有经过合理筛选、恰当组织，仅经过“一讲一做”是很难发挥出应有的效果的。相反，对于课本习题，因为简单熟悉，不需要在解答上花太多精力，所以师生可以在解题前后集中精力进行观察、比较、归纳、抽象、同化、重建、感悟等思维活动，会有事半功倍之效。但其前提是，教师必须找准学生认知、思维发展与课本习题的契合点，对习题加以合理变式、恰当引申，再在课堂上有序组织、精讲点拨。以下三个案例是笔者的教学实践，仅供参考。

三、教学案例

1.一题三用，完善学生知识体系。

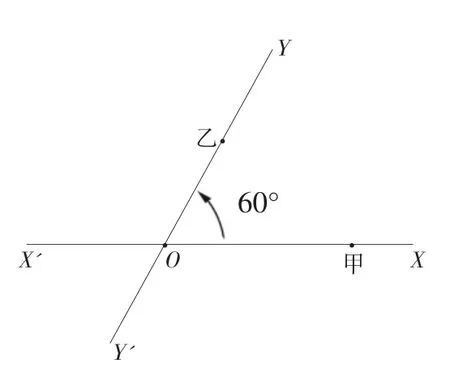
图1

【例1】（必修5 习题1.3 第8题）如图1，有两条相交成60°角的 直 路 XX′ ，YY′，交点是O，甲、乙分别在OX，OY 上，起初甲离O 点3km，乙离O 点1km。后来甲沿XX′的方向，乙沿YY′的方向，同时用4km/h 的速度步行。

（1）起初两人的距离是多少？

（2）t 小时后两人的距离是多少？

（3）什么时候两人的距离最短？

【教学设计】此题在复习解析几何的“直线方程”时作引入题目让学生解答，目的是巩固基础知识，体会解析法是解决长度度量问题的基本方法。复习“平面向量”时再次引入，要求学生分别从向量的几何特征（有向线段）和代数特征（坐标表示）两方面独立求解。复习“解三角形”时，再一次要求学生用解三角形的知识求解。教师适时点评，引导学生归纳知识间的联系、比较方法的繁简、体会问题解决过程的异同。第三次评讲时辅以如下追问：为何解三角形需分类讨论，而前两种不需分类讨论？分类讨论得出的距离表达式为何形式上完全一致？通过一题三解，以后遇到距离的度量问题，你有何反应？

【设计说明】从学生学习相关模块的先后顺序上看，“解析法”在“平面向量”之前，“平面向量”又在“解三角形”之前，而这道课本习题在教材体系中是“解三角形”的习题，在复习教学时让其由后而前“归位索源”，可以达到激活知识点、串成知识链、形成知识表征系统，充实学生认知结构的目的。经历此过程，学生对长度距离等度量问题的表征将有策略性的认知，对解决这类问题的能力也有提升。

2.一题多变，发展学生推理能力。

【例2】（必修4“三角恒等变换”复习题第18 题）如图2，在半径为R、圆心角为60°的扇形AB 弧上任取一点P，作扇形的内接矩形PQMN，使点Q 在OA 上，点M，N 在OB 上，求这个矩形面积的最大值及相应的∠BOP 值的大小。

【教学设计】在复习“三角函数”的运用时引入题目，先让学生猜想取得最大值时点P 在圆弧上的位置，然后让学生通过解答修正和验证猜想。完成后，引导学生思考面积的最值与取点P 的位置两者之间具有必然性。之后进行如下变式教学：

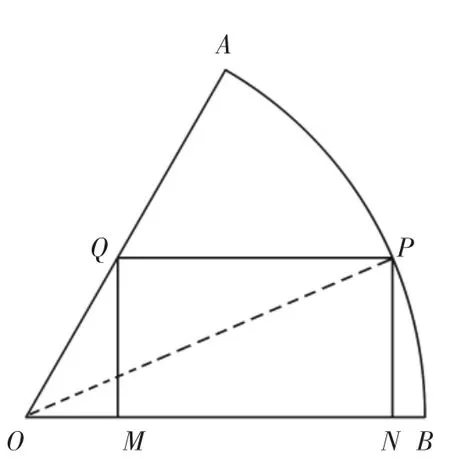
图2

（1）用动画演示圆心角从锐角经直角变成钝角的过程，让学生观察内接矩形PQMN 四个顶点在扇形边界上的变化情况。

（2）出示圆心角为120°的扇形，要求学生画出其内接矩形PQMN，并一步猜想矩形面积最大时，圆弧上的顶点的位置。

（3）对比观察圆心角为60°和120°的两扇形，对于它们的面积最大内接矩形，猜想它们在面积的数量上、图形形状上分别有怎样的联系，并思考这种联系的根据。

（4）若将题目中“相应的∠BOP 值的大小”去掉，或者将问题改成“求这个矩形面积的最大值及相应点P 在圆弧上的位置”，你打算如何做？是否还能像之前的解答那样，自然地设“∠BOP=θ”作为建立面积函数的自变量？

【设计说明】观察的任务是要学生直观感知到矩形的长和高两要素在扇形两边的横向或斜向放置具有等效性，以便猜出最值产生条件，目的在于鼓励学生大胆猜想，培养学生合情推理的能力；修正验证的过程是让学生明白图形的对称性与面积最大值两者之间有必然联系，发展学生的直觉思维能力。

变式（1）是让学生通过观察，发现扇形形状的改变会使矩形四个顶点在扇形的分布情况也发生改变，具体过程是：∠AOB 为锐角时，弧上1 点两条半径3 点→∠AOB 为直角时，弧上1点两半径各1 点圆心1 点→∠AOB 为钝角时，圆心上的点运动到半径反向延长线上。

观察的目的是为变式（2）的猜想做铺垫，只猜不证既为节省时间也为降低难度，因为此时学生未必找到建立面积函数的入口，学生猜完之后，引出变式（3），学生若遇到困难，则以“大扇形是小扇形的2 倍”的图形直观为切入点，引导学生实现类比、迁移等认知活动。继而提出，如果问题是“求圆心角为120°的扇形的内接矩形面积的最大值”，该如何解决。目的是让学生明白“将120°的扇形对折，变成两个60°的扇形”，体现的是转化与化归思想。在此过程中，学生经历观察、猜想、验证、类比、迁移、转化等思维认知活动。

变式（3）完成后，在圆心角为60°扇形中改变内接矩形四个顶点位置，要求学生观察变化过程，四个顶点对矩形的影响有无“先后之别和强弱之分”，得出“地位均等”的结论，然后提出变式（4），目的是让学生发现题目设问方式的提示性。

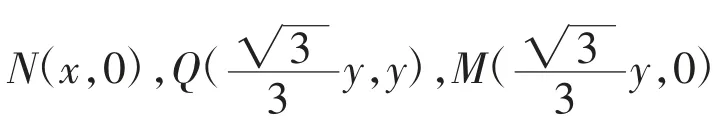
由此可见，课本习题在选编过程中，编者会人为降低难度，为学生搭建“脚手架”，这也许是课本习题简单基础的原因之一。这也说明，高三复习教学时，教师既要培养学生从题目外在形式去发现解题信息的能力，更应培养他们从题目内容上去辨别知识，并能根据需要选择恰当的表征形式的能力，而后者关系到学生对知识的理解程度、问题解决的能力和自我监控能力的提升。它们应该成为高三复习教学考量的重点，这也许是课本习题最重要的教学价值。

3.类比对称，感受数学魅力。

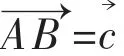
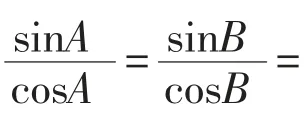
【设计说明】对于本题，学生一般会从数量积的定义入手，引入三角形的内角，再用正余弦定理进行代换完成证明。在教学时，教师可以设法制造审美冲突，激发学生审美欲望，具体实施过程是，待学生解答完成后，引导他们观察题目条件，让其发现轮换对称，再比对结论，使之感受到题目的条件和结论具有和谐对称的美学性质。学生在有“美感”的同时，通过对比自己解答过程或展示参考答案，产生“不顺眼”感觉，从而形成冲突，激发欲望。完成后再引导学生比对条件、解答所用知识各自所属模块，探索隐藏在题目内部的和谐美。

概而言之，课本习题是内蕴深厚的资源宝库，不该轻视。高三复习，与其对外来资料实行“拿来主义”，不如潜心研究课本习题，充分发挥其教育功能和潜在价值。