基于均匀化分布的Chebyshev映射系统构建及特性分析

黄滨 保利勇 丁洪伟

摘 要：针对传统Chebyshev映射所呈现的值域边界双峰的分布特性，为满足优化理论中序列均匀分布的需求，结合Chebyshev映射概率密度函数进行数理推导，将得到的随机变量函数与原映射级复合成新的系统。通过对比研究表明，系统具有良好的均匀分布特性、遍历特性、平衡性和较低的复杂度，所产生序列的随机误差小，相似度高。最后将系统应用于优化算法中的初始化种群阶段，进一步说明了所做的均匀化分布系统在改善原序列均匀分布特性的效果是显著的。

关键词：混沌;动力学系统;Chebyshev映射;均匀化分布;混沌特性

中图分类号：TP27

文献标志码：A

Abstract：Concerning the bimodal distribution characteristics of the range boundary presented by the traditional Chebyshev mapping， in order to meet the requirements of homogenized distribution of sequences in optimization theory， the mathematical equation was given by using the probability density function of Chebyshev mapping， and a new system was constructed by combining with the original mappinginto a new system.The comparative study shows that the system has good homogenized distribution characteristic， ergodic characteristic， balance and low complexity， and the random error of the generated  sequences is small and the similarity is high. Finally， the system is applied to the initialization population stage of the optimization algorithm， and it is further shown that the homogenized distribution system has a significant effect on improving the homogenized distribution characteristic of the original mapping.Key words： chaos; dynamics system; Chebyshev mapping; homogeneous distribution; chaotic characteristic

0 引言

混沌是一种类随机的运动方式，它通常包含在确定性的非线性动力学系统中，它所能实现的不同迭代轨迹集中体现在随机性、遍历性、初值敏感性和不可预测性等混沌特性。传统Chebyshev映射可以通过控制相关参数使其进入混沌状态，相比Tent映射、Logistic映射等一维映射，它的值域范围更大且具有良好的混沌特性。目前，均匀化分布处理的方法有很多。

文献[1]根据现有理论通过概率密度函数将二次多项式构造出反三角映射函数;文献[2]通过变换函数的方式改造了Logistic映射，使其在（0，1）内满足均匀分布，并且利用了直方频数图、信息熵和平衡型等指标对均匀化效果进行评价。这就对在保有混沌特性基础上，如何有效扩宽满足均匀分布的值域范围、对满足等可能取值要求较高的优化问题、仿生算法等相关领域，提出了更高的要求。

本文采用具有更大值域范围的Chebyshev映射，首先通过求解均匀优化Chebyshev映射概率密度函数微分方程，推导出随机变量函數，使其在区间[-1，1]内成为均匀化分布Chebyshev映射（Homogeneous Distribution Chebyshev，HDC）系统。进一步，本文采取仿真实验的方式，将构建的均匀化分布系统与近年来性能较好的同类系统作出定量定性的对比分析，全面逐一比较了不同系统的直方频数图、平衡性、信息熵、近似熵、相关性和功率谱密度。最后，通过一个具体的人工蜂群算法初始化种群阶段的应用，更为有力地说明本文提出的均匀化分布系统在改善系统的均匀分布特性上是显著有效的。

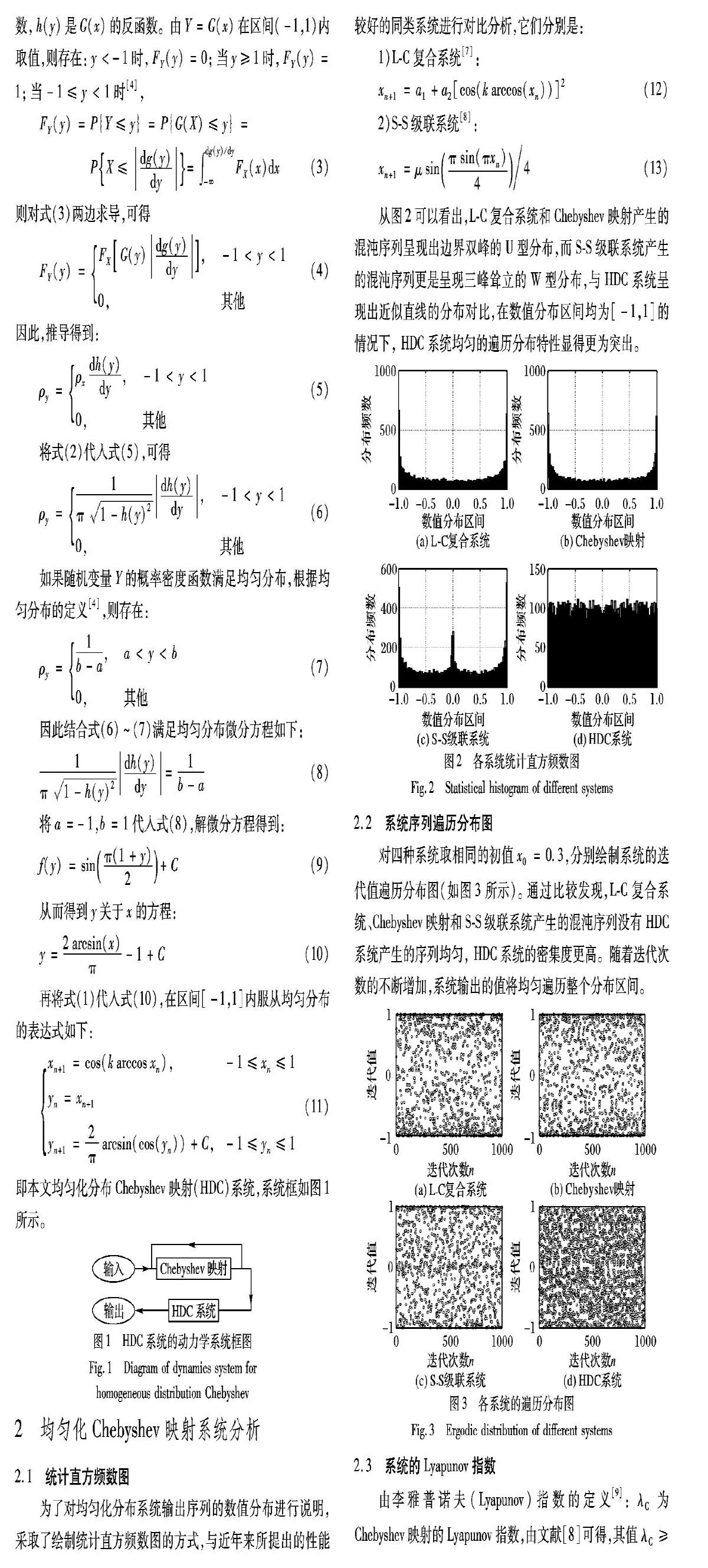
从图2可以看出，L-C复合系统和Chebyshev映射产生的混沌序列呈现出边界双峰的U型分布，而S-S级联系统产生的混沌序列更是呈现三峰耸立的W型分布，与HDC系统呈现出近似直线的分布对比，在数值分布区间均为[-1，1]的情况下， HDC系统均匀的遍历分布特性显得更为突出。

2.2 系统序列遍历分布图

对四种系统取相同的初值x0=0.3，分别绘制系统的迭代值遍历分布图（如图3所示）。通过比较发现，L-C复合系统、Chebyshev映射和S-S级联系统产生的混沌序列没有HDC系统产生的序列均匀， HDC系统的密集度更高。随着迭代次数的不断增加，系统输出的值将均匀遍历整个分布区间。

2.3 系统的Lyapunov指数

由李雅普诺夫（Lyapunov）指数的定义[9]：λC为Chebyshev映射的Lyapunov指数，由文献[8]可得，其值λC≥ln 2;λL为均匀化分布系统的李雅普诺夫指数，yn的取值在（-1，1）区间，当yn=0时，λL≥ln（2/π）。系统李雅普诺夫指数的计算[10]如下式：

设定L-C复合系统的参数a1=1，a2=-2， S-S级联系统的参数μ=0，其中将系数k控制在区间[0，200]，初值x0=0.33，绘制几类系统的Lyapunov指数图。如图4所示，随着系数k的不断递增，L-C复合系统与Chebyshev映射表现出了相似的变化曲线，且前者的Lyapunov指数更高，而HDC系统的Lyapunov指数在原映射发生微弱起伏的變化。因此，虽然HDC系统不如L-C复合系统和Chebyshev映射的Lyapunov指数高，但该系统仍然保持了混沌系统的特性，也验证了理论推导中Lyapunov指数为正的结论。

2.4 均匀性与复杂度

信息熵作为衡量序列混乱程度的特征参数[12]，用于表征信源不确定的程度，信息熵越接近于最大信息熵则系统均匀性越好。而混沌序列的复杂度可用近似熵（ApEn）算法来衡量，ApEn的取值越大，混沌序列的复杂度越高[13]。

混沌的迭代次数设为n=50000，将序列值域设定不同的M个区间个数计算信息熵;对不同的混沌序列的长度依次取L=1000，2000，4000，5000，10000，k均取2，

初值x0为0.33，进行近似熵求解，计算结果如表1～2。

信息熵随着区间个数M的增多，不同系统的信息熵均得到提升，L-C复合系统、S-S级联系统和Chebyshev映射的信息熵相差不大，而HDC系统的信息熵变化最为显著，无限接近最大信息熵。

此外，对与系统的近似熵而言，HDC系统与Chebyshev映射的近似熵接近，基本没有发生变化，且与L-C复合系统的近似熵存在较大差异。

这是因为HDC系统产生序列的均匀化分布特性高，导致了序列本身的值较为平均，复杂度有所降低。因此通过信息熵与近似熵的评价，可以进一步说明本文对系统产生序列的均匀化分布处理是有效的。

2.5 平衡性

下面通过二值量化[11]的方式，对四个不同映射系统产生序列的平衡性进行研究。通过随机的方式选取50个不同初值，判决门限设定为0，其中L-C复合系统的参数a1=1，a2=-2，而S-S级联系统的参数μ=4，计算平衡性均值并绘制出其曲线，结果如图5所示。可以看出，S-S级联系统在序列长度L<100时曲线变化趋于先下降后上升的振荡状态，在5001000以后开始收缩，接近3000时才开始接近于0;而Chebyshev映射和HDC系统的平衡曲线在L<500时呈现出相似的波动状态，在L>500以后均表现出随序列长度的增加趋于稳定，显然HDC系统的均值更接近于0。

2.6 相关性

自相关特性是用于描述序列产生随机误差项相关性指标，而互相关特性是运算结果反映两个序列之间相似性的量度[3]。

对四种系统的序列取相同的长度为500，初值x0=0.8，仿真四种系统的自相关特性。如图6所示，四种系统均表现出了在相关间隔为0时的尖锐自相关特性。L-C复合系统、Chebyshev映射和S-S级联系统的自相关值均为0.5，HDC系统自相关值接近于0.1。这种差别也体现了HDC系统产生序列的随机误差小，即序列的均匀性是良好的。

选取初值分别为x0=0.1，y0=0.5，序列长度为1000，对四种系统的互相关特性进行仿真。从图7中可见，四种系统的互相关值都在0附近，HDC系统与其他三种系统对比，互相关值的波动幅度更小，集中在（-0.05，0.05）区间，即随机生成的序列的相似程度与均匀化分布处理后有很大关联。

2.7 功率谱密度

功率谱密度是随机动态激励下系统产生响应的统计结果，实际上刻画的是随机过程的强度。Welch方法是一种修正周期图功率谱密度估计方法，它通过选取的窗口对数据进行加窗处理，先分段求功率谱之后再进行平均[14]。

如图8所示，设定迭代次数为5000，初值x0=0.5，做了归一化处理后相对最大值来说，其他点的峰值都是负值。可以看到，前三种系统的功率谱密度曲线在总体走势上虽然保持了一致，但在更细节的形状上差异也不小，功率/频率值保持在（-5，-15）内，而HDC系统的功率/频率值的高值较低，集中在（-15， -20）。因此，前三种系统得到的功率谱分辨率越高，同时方差加大;HDC系统方差变小，但功率谱分辨率较低。对于随机产生序列的方差，HDC系统产生的序列方差更小，均匀分布性明显。

3 应用仿真

为进一步验证本文HDC系统的均匀分布性能，通过对人工蜂群算法初始化种群阶段采取的蜜源分布分析[14]。选取Bohachevsky函数对其初始蜜源分布进行研究。Bohachevsky函数本身表现出非线性多模态的函数特征，此起彼伏的山峰出现存在跳跃性，具有开阔的搜索立体空间。仿真条件设置为迭代次数为1000，

取初值x0为0.33，k值取2，绘制出四种系统初始蜜源分布XY视图。如图9所示，L-C复合系统和Chebyshev映射初始化的蜜源均集中在边界处，中部区域稀疏;而S-S级联系统初始化的蜜源大致呈现“十字”的分布规律，分布不均匀;经过HDC系统初始化的蜜源分布比其他三种系统初始化的蜜源更加均匀，验证了HDC系统可以使解集更加均匀分布在函数的解空间里。

4 结语

本文基于混沌映射迭代值遍历整个值域区间时均匀优化的需求，通过数理推导出随机变量函数与原映射合成的一种均匀优化Chebyshev映射的系统，并对其平衡性、复杂度、相关性和功率谱密度等进行仿真与评价。分析结果表明，均匀化分布的系统有效解决了值域边界双峰型的分布问题，序列在整个区间趋于均衡。仿真结果表明：平衡曲线随着序列长度增加更加均匀和稳定，复杂度指标的降低也充分说明了系统均匀性良好，产生序列的随机误差小，不同序列间相似程度高，可以在优化算法中使得初始化种群的分布趋于均匀遍历。因此，本文引入的动力学系统在改善系统均匀分布的特性是有效的。