多标签学习中基于互信息的快速特征选择方法

徐洪峰 孙振强

摘 要：针对传统的基于启发式搜索的多标记特征选择算法时间复杂度高的问题，提出一种简单快速的多标记特征选择（EF-MLFS）方法。首先使用互信息（MI）衡量每个维度的特征与每一维标记之间的相关性，然后将所得相关性相加并排序，最后按照总的相关性大小进行特征选择。将所提方法与六种现有的比较有代表性的多标记特征选择方法作对比，如最大依赖性最小冗余性（MDMR）算法和基于朴素贝叶斯的多标记特征选择（MLNB）方法等。实验结果表明，EF-MLFS方法进行特征选择并分类的结果在平均准确率、覆盖率、海明损失等常见的多标记分类评价指标上均达最优;该方法无需进行全局搜索，因此时间复杂度相较于MDMR、对偶多标记应用（PMU）等方法也有明显降低。

关键词： 多标签学习;特征选择;互信息;标记相关性

中图分类号：TP181

文献标志码：A

Abstract：Concerning the high time complexity of traditional heuristic search-based multi-label feature selection algorithm， an Easy and Fast Multi-Label Feature Selection （EF-MLFS） method  was proposed. Firstly， Mutual Information （MI） was used to measure the features and the correlations between the labels of each dimension; then， the obtained correlations were added up and ranked; finally， feature selection was performed according to the total correlation. The proposed method was compared to six existing representative multi-label feature selection methods such as Max-Dependency and Min-Redundancy （MDMR） algorithm， Multi-Label Naive Bayes （MLNB） method. Experimental results show that the average precision， coverage， Hamming Loss and other common multi-label classification indicators are optimal  after feature selection and classificationby using EF-MLFS method. In addition， global search is not required in the method， so the time complexity is significantly reduced compared with MDMR and Pairwise Mutli-label Utility （PMU）.

Key words：  multi-label learning; feature selection; mutual information; label correlation

0 引言

在传统的监督学习任务中，每个样本被默认为只具有一种语义信息，也就是只包含一种分类标签。然而，这样的假设往往与现实世界的真实情况不符，例如，在图片分类任务中，一张沙滩风景图片往往同时包含“大海”“轮船”“落日”等景物，由此可见，使用单一标记无法充分表达其语义信息，同样使用传统的单标记分类方法将很难对这种情况进行准确的分类。多标记学习（Multi-label Learning）[1]應运而生，并在信息检索[2]、生物信息[3]、药物研发[4]以及传统中医诊断[5-6]等领域取得了出色的成果。

与传统监督学习相比，多标记学习的输入输出空间维度更大。在大多数情况下，相较于单标记数据集，为了支持多个标记的学习任务，多标记数据的特征往往更加冗余和稀疏。然而，过高的特征维度将会导致维度灾难的发生，这将使得多标记学习任务效率变得低效和困难。因此，有效地解决多标记学习任务中的维度灾难问题变得十分关键。

特征选择方法是直接从原始特征空间选择特征子集，因此保留了原始特征的物理含义，具有极强的可解释性和易操作性，尤其在高维数据集和有限数据集的数据预处理任务中具有十分重要的地位。特征选择方法根据一定的评价标准，从原始特征空间中选择一组最优特征子集，从而降低特征维度，提高分类性能。目前比较常见的评价标准有：依赖性度量、距离度量和信息度量。同时，区分多标记学习任务与传统学习框架的特点就是其不同标记之间往往具有相关性，而对这些相关性的有效利用将会有效降低学习任务的难度。根据朱越等[1]的研究，目前标记相关性可以分为一阶相关性、二阶相关性和三阶相关性。

目前，大部分的研究工作均为对特征选择过程中使用的“最大相关性，最小冗余性”标准中的相关性和冗余性进行相关分析，从而导致了计算资源的浪费。本文在进行一系列实验时观察到，大多数多标记数据集由于其特征空间的高维性和稀疏性，其特征与特征之间的冗余程度往往很小。因此在多标记特征选择问题当中，冗余性的加入往往无法提升特征选择的效果，反而会增加不必要的计算资源的浪费。本文提出了一种简单快速的多标记特征选择（Easy and Fast Multi-Label Feature Selection， EF-MLFS）方法，是一种只利用特征标记相关性的极简且效果很好的特征选择算法。

1 相关工作

在多标记特征选择发展的几十年里，涌现出了许多杰出的工作。为了更好地区分每种方法的相似和不同之处，相关学者对已有的特征选择方法进行了分类，目前广泛认可的分类方法有两种：第一种分类方法从特征选择的策略角度出发，將特征选择方法分为封装（wrapper）方法[7]、过滤（filter）方法[8]和嵌入（embedded）方法[9];第二种分类方法从标记利用角度出发，将特征选择方法分为有监督（supervised）[7]、无监督（unsupervised）[10]和半监督（semi-supervised）[11]特征选择方法。

本文主要利用互信息（Mutual Information， MI）和标记相关性（Label Correlation）

进行特征选择。在利用信息论进行特征选择的众多方法中，最经典的两种方法被称为互信息特征选择（MI Feature Selection， MIFS）[11]和 最大相关最小冗余性（maximum Relevance Minimum Redundancy， mRMR）[12]。在MIFS方法中利用互信息估计某一维特征的信息量，并利用“贪心”搜索方法选择最优特征子集;在mRMR方法中选择出的特征子集具有“最大相关性，最小冗余性”的特点。除此之外，还有许多学者利用信息论进行特征选择的优秀工作，例如Lin等[13]提出最大独立性最小冗余性（Max-Dependency and Min-Redundancy， MDMR）算法;Lee等[14]利用多元互信息提出一种对偶多标记应用宋国杰等[8]提出一种基于最大熵原理特征选择方法;朱颢东等[15]提出一种优化的互信息特征选择算法等。

除此之外，近几年利用标记信息进行特征选择的方法也不断涌现。例如，Wang等[16]通过最大化非独立分类信息进行特征选择;Brown等[17]提出一种针对信息论的联合特征选择框架;蔡亚萍等[18]提出一种利用局部标记相关性的特征选择方法;杨明等[19]提出一种结合标记相关性的半监督特征选择方法;Braytee等[20]提出一种基于非负矩阵分解的特征选择方法;Liu等[21]提出一种基于标记相关性的加权特征选择方法;Monard等[22]提出了一种根据原始标记相关性进行标记空间重构的方法。

2 相关知识

2.1 互信息与最大相关最小冗余性（mRMR）

信息论[23]已经被广泛应用于诸多领域。作为信息理论的重要组成部分，互信息是一种衡量相关性的有效手段，描述了两组变量之间信息共享的程度。例如，两组随机变量A和B之间的互信息可以定义如下：

其中： p（a，b）为A、B的联合概率分布。

mRMR作为特征选择的经典算法，已经演变出许多变种。

mRMR的作者认为“前m个最好的特征不一定是最好的m个特征”，因为前m个特征可能存在大量相关信息，这些特征之间具有高度相关性，所以作者提出mRMR框架，并将其形式化描述为：

2.2 评价指标

考虑与其他方法的比较，本文中选取了海明损失、One-Error、覆盖率、排序损失和平均准确率作为评价指标。

本文将统一使用yi∈L表示真实标记， y′i表示对特征向量xi的预测标签，N表示样本数量，m表示标记维度。

其中：为异或运算。该指标计算的是在所有N*m个预测标记中犯错的比例，其值在0～1，指标值越小越好。该指标计算预测结果中最可能的标记预测错误的比例，其值在0～1，指标值越小越好。该指标反映的是在预测的标记序列中，要覆盖所有的相关标记需要的搜索深度，其值越小表示所有相关标记均被排在比较靠前的位置。

4）排序损失（Ranking Loss， RL）：其中： yi和i分别表示xi的相关标记集和无关标记集，该指标计算相关与无关标记对出现错误的比例，指标值越小越好。该指标衡量的是按照预测值排序的标记序列中，被排在相关标记之前的标记仍是相关标记的情况，指标值越大越好在多标记特征选择问题中，“最大相关性，最小冗余性”是一个经典且证实有效的特征选择标准目前该标准的优化算法仍然是建立在最大相关性和最小冗余性的基础上。

但对主要多标记数据集上进行实验时发现，特征间的冗余性或许并不是特征选择过程中所必须考虑到的因素，而特征与标记相关性衡量可能对特征选择结果起到决定性作用。同时，忽略特征间冗余性的影响，将会大幅简化算法运算过程，从而提高算法性能。根据“奥卡姆剃刀”原则忽略特征冗余度的影响，不仅未降低算法性能，反而在大多数数据集上大幅提升了特征选择的效果。

在多数的多标记数据集中，标记特征相关性往往可以提供重要信息，利用这些信息将有效降低学习任务的难度，同时提升学习结果的鲁棒性。

在多标记数据集中，特征往往是连续或高度离散的，同时十分稀疏。因此，无论是使用互信息，还是用欧氏距离的方法衡量特征间的冗余度，其结果可以发现特征与特征间的冗余性几乎为零，其效果往往微乎其微甚至对特征标记相关性的使用产生负面影响。同时，多标记的监督学习中最重要的就是对标签的有效利用，

因此本文从最简单设想切入，利用互信息来衡量特征标记相关性，同时忽略掉冗余性的影响，最后依据特征标记相关性的大小来进行特征选择。

首先，使用互信息计算每一维特征标记之间的相关性矩阵R：其中：Ri， j为相关性矩阵的每一个元素; fi表示第i维特征向量;lj表示第j维标记向量。假设所选数据集中有N维特征向量，K维标记向量，则矩阵R为一个N*K的矩阵。该矩阵中蕴含的就是特征标记相关性信息，数值越大代表特征与标记之间的相关性越强。如果某一维度特征与所有标记相关性的总和最大，则它就是最重要的特征，根据重要性进行排序，将会得到一个特征重要性的有序向量。

根据以上假设，本文将矩阵R按列相加，得到特征重要性向量I：最后根据向量I的大小从大到小进行排序并记录相应的特征维度标记，得到最后的特征重要性排序向量I-Rank。

4 实验与分析

为了评测EF-MLFS算法的性能，本文将在6个真实数据集上与其他6种特征选择算法进行对比实验。

实验采用多标记最近邻（Multi-Label K Nearest Neighbors， ML-KNN）[24]作为分类算法对特征选择后的数据集进行评估，并将近邻数量k设置为15。

对比算法的参数设置依照原论文给出的推荐参数进行设置。ML-KNN相关代码可以在LAMDA实验室主页进行下载（http：//lamda.nju.edu.cn/CH.MainPage.ashx）。

4.1 实验数据及设置

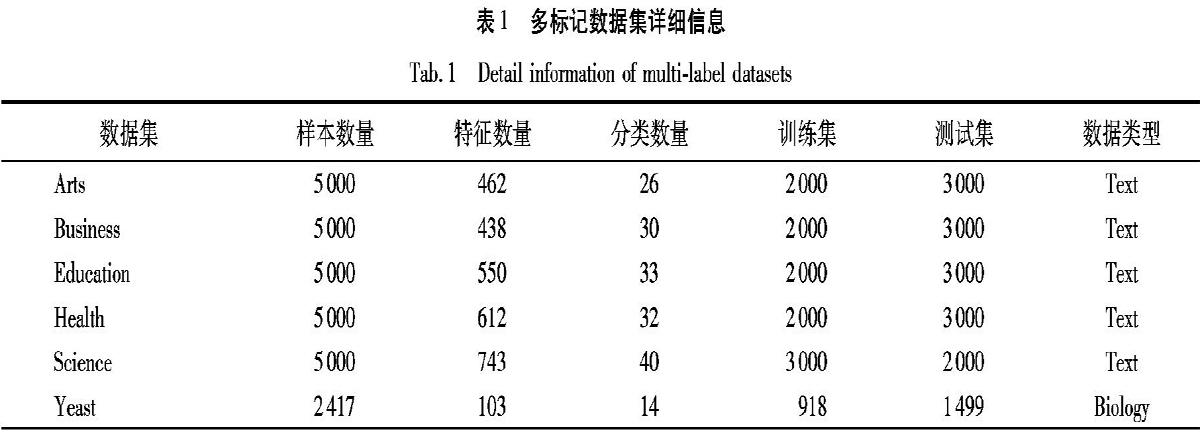
本实验数据主要来自于公开多标记数据集网站MULAN（http：//mulan.sourceforge.net），其中Arts、Business、Education、Health、Science五个网页数据集属于Yahoo数据集，每个数据集含5000个样本，提取的特征表示不同的词在文本中的频率，标记表示文本的类别信息;Yeast为生物数据集，包含2417个样本，其特征维度是103。表1列出了所使用数据集的详细信息。同时，为比较EF-MlFS算法的性能，实验将与基于朴素贝叶斯的多标记特征选择（Multi-Label Naive Bayes， MLNB）[25]、PMU[14]、

MDDMspc（Mutli-label Dimensionality Reduction via Dependecnce Maximization with Uncorrelated Feature Constraint）[26]

、MDDMproj（Multi-label Dimension Reduction via Dependence Maximization with Uncorrelated Projection Constraint）[26]、MDMR[13]以及COMI（Convex Optimization and MI）[27]6種多标记特征选择算法在上述评价指标上进行比较，其中COMI方法[27]为Lim等于2017年提出的一种基于互信息与凸优化的方法，该方法改进了以往基于启发式搜索的特征选择策略，在mRMR方法的基础上利用互信息计算相关性与冗余性，是目前基于互信息进行特征选择的众多方法中比较有代表性的一种。

4.2 实验结果与分析

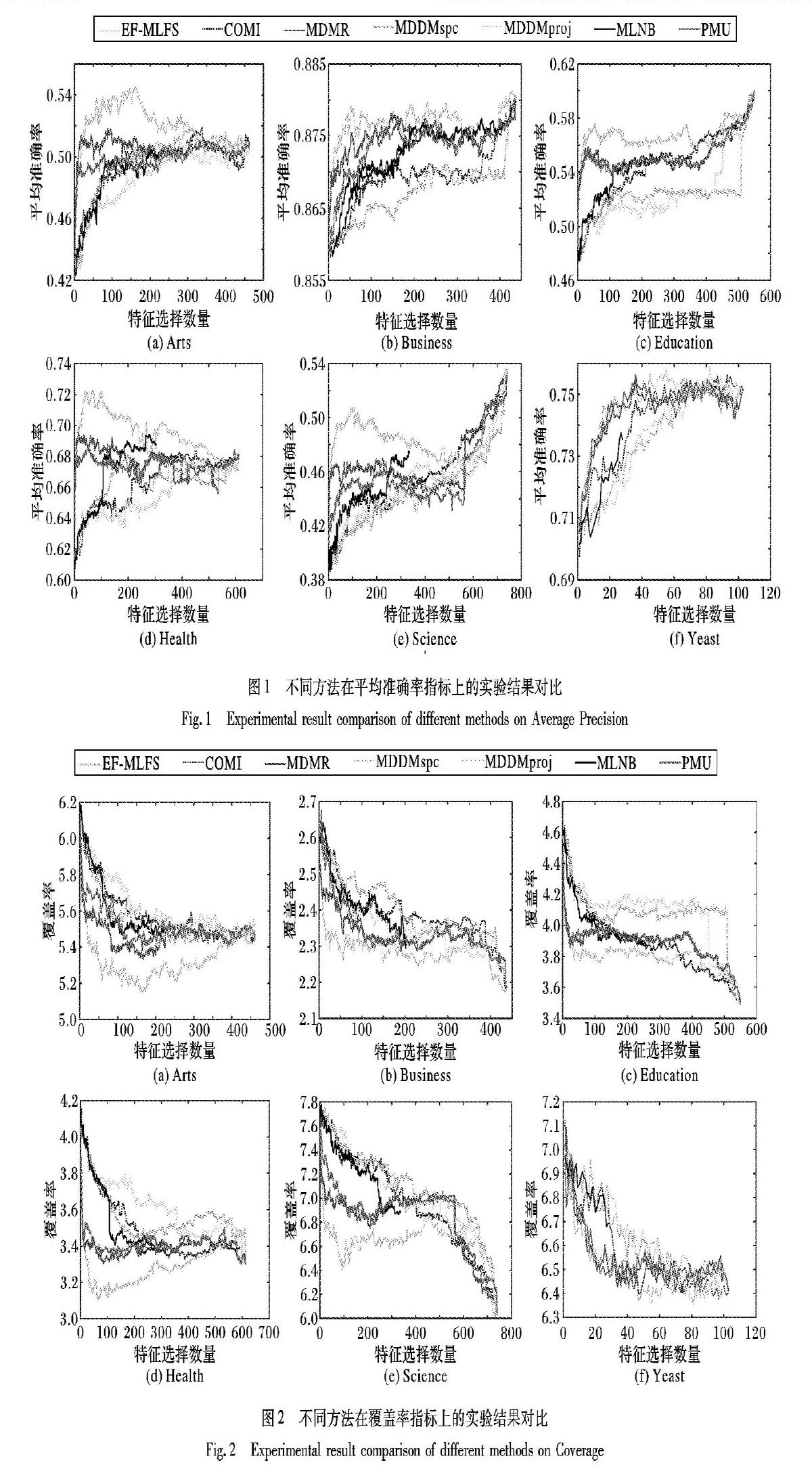
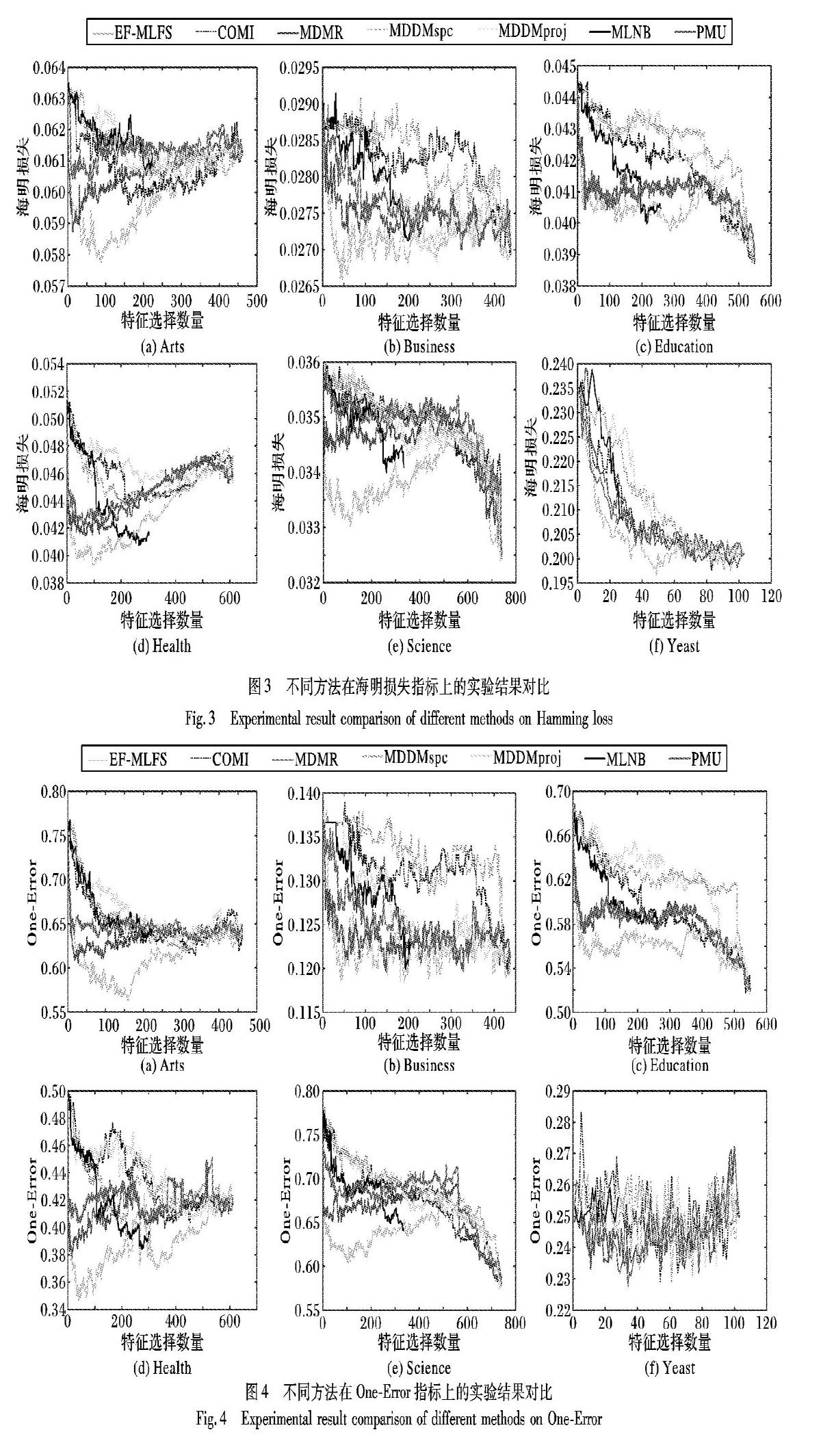
为对比各算法所能达到的最好分类效果，本文实验将最优特征子集维度从1调整至最大并绘制得分曲线，虽然MLNB算法最大特征数量与其他算法不同，但仍具有可比性。

1）实验曲线在前几个特征呈明显上升或下降趋势，在达到最优值后呈相反趋势变化，说明特征选择算法对大多数数据集有效，并且可以选择出效果明显好于使用所有特征进行分类的特征子集。

2）EF-MLFS方法在Arts、Business、Education、Health、Science、Yeast共6个数据集上的5种评价指标均可以达到最优的效果，同时在Arts与Health等文本数据集上效果也非常显著，说明本文方法泛化效果与选择结果均优于其他方法。

3）MDDM是一种基于矩阵分解的方法，因此其在时间性能上有明显优势。考虑到EF-MLFS方法几乎不需要任何复杂的矩阵运算，大部分时间消耗来自于计算特征-标记相关性矩阵，因此EF-MLFS方法相较于MDMR、MLNB、PMU三种方法在时间性能上均有三个量级的提升效果。

4）EF-MLFS方法具有最高的性能时间比，可以在提高性能的前提下，大幅提高算法效率。

5）COMI方法虽然也是一种基于互信息的多标记特征选择方法，但原文中并未对其数据预处理进行详细描述，同时其特征选择过程中涉及到全局优化的过程，虽然较传统的启发式搜索方法在时间性能上有较大提升，但在性能和时间上均未达到最优效果。因此EF-MLFS方法虽然简单，但是仍可达到较优的性能。

总体来讲，EF-MLFS算法在上述对比指标下均有不错的表现，尤其EF-MLFS算法是一种快速有效的特征选择方法，该方法具有更强的鲁棒性和更好的泛化性，可以适应多个应用场景并找到最优特征子集。同时，上述实验也验证了第3章中关于特征空间冗余性的假设。

5 结语

本文在针对经典特征选择框架“最大相关性，最小冗余性”进行研究时发现，在大多数公开的多标记数据集中，冗余性的加入并不能有效提高多标记特征选择的效果，反而会加大特征选择过程的运算量，降低选择效率。因此，根据“奥卡姆剃刀”的核心原则“如无必要，勿增实体”的思想，将冗余性去掉，只利用特征标记相关性进行多标记特征选择，并得到了很好的结果。

但是，本文仍有诸多不足之处，需要在未来的工作当中进行改进。例如，如何有效定量验证数据当中冗余性是否必要，如何更加准确地衡量特征标记相关性，以及如何更加有效地挖掘特征标记相关性当中蕴含的信息。同时针对标记相关性的研究工作也日益增多，对如何有效利用标记之间的相关性也是未来的研究方向。

参考文献（References）

[1] 朱越， 姜远， 周志华. 一种基于多示例多标记学习的新标记学习方法[J]. 中国科学： 信息科学， 2018， 48（12）： 1670-1680. （ZHU Y， JIANG Y， ZHOU Z H. Multi-instance multi-label new label learning[J]. Scientia Sinica （Information）， 2018， 48（12）： 1670-1680.）

[2] SCHAPIRE R E， SINGER Y. BoosTexter： a boosting-based system for text categorization[J]. Machine Learning， 2000， 39（2/3）： 135-168.

[3] DIPLARIS S， TSOUMAKAS G， MITKAS P A， et al. Protein classification with multiple algorithms[C]// Proceedings of the 2005 Panhellenic Conference on Informatics， LNCS 3746. Berlin： Springer， 2005： 448-456.

[4] 彭利紅， 刘海燕， 任日丽， 等. 基于多标记学习预测药物靶标相互作用[J]. 计算机工程与应用， 2017， 53（15）： 260-265. （PENG L H， LIU H Y， REN R L， et al. Predicting drug-target interactions with multi-label learning[J]. Computer Engineering and Applications， 2017， 53（15）： 260-265.）

[5] LIU G P， LI G Z， WANG Y L， et al. Modelling of inquiry diagnosis for coronary heart disease in traditional Chinese medicine by using multi-label learning[J]. BMC Complementary and Alternative Medicine， 2010， 10（1）： No.37.

[6] DAI L， ZHANG J， LI C， et al. Multi-label feature selection with application to TCM state identification[J/OL]. Concurrency and Computation： Practice and Experience， 2018： No.e4634. [2019-01-10]. https：//onlinelibrary.wiley.com/doi/abs/10.1002/cpe.4634.

[7] GUYON I， ELISSEEFF A. An introduction to variable and feature selection[J]. Journal of Machine Learning Research， 2003， 3： 1157-1182.

[8] 宋国杰， 唐世渭， 杨冬青， 等. 基于最大熵原理的空间特征选择方法[J]. 软件学报， 2003， 14（9）： 1544-1550. （SONG G J， TANG S W， YANG D Q， et al. A spatial feature selection method based on maximum entropy theory[J]. Journal of Software， 2003， 14（9）： 1544-1550.）

[9] GUYON I， WESTON J， BARNHILL S， et al. Gene selection for cancer classification using support vector machines[J]. Machine Learning， 2002， 46（1/2/3）： 389-422.

[10] DY J G. BRODLEY C E. Feature selection for unsupervised learning[J]. Journal of Machine Learning Research， 2004，5： 845-889.

[11] BATTITI R. Using mutual information for selecting features in supervised neural net learning[J]. IEEE Transactions on Neural Networks， 1994， 5（4）： 537-550.

[12] PENG H， LONG F， DING C. Feature selection based on mutual information criteria of max-dependency， max-relevance， and min-redundancy[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence， 2005， 27（8）： 1226-1238.

[13] LIN Y， LIU J， LIU J， et al. Multi-label feature selection based on max-dependency and min-redundancy[J]. Neurocomputing， 2015， 168： 92-103.

[14] LEE J， KIM D. Feature selection for multi-label classification using multivariate mutual information[J]. Pattern Recognition Letters， 2013， 34（3）： 349-357.

[15] 朱顥东， 陈宁， 李红婵. 优化的互信息特征选择方法[J]. 计算机工程与应用， 2010， 46（26）： 122-124. （ZHU H D， CHEN N， LI H C. Optimized mutual information feature selection method[J]. Computer Engineering and Applications， 2010， 46（26）： 122-124.）

[16] WANG J， WEI J， YANG Z， et al. Feature selection by maximizing independent classification information[J]. IEEE Transactions on Knowledge and Data Engineering， 2017， 29（4）： 828-841.

[17] BROWN G， POCOCK A， ZHAO M， et al. Conditional likelihood maximization： a unifying framework for information theoretic feature selection[J]. Journal of Machine Learning Research， 2012， 13： 27-66.

[18] 蔡亚萍， 杨明. 一种利用局部标记相关性的多标记特征选择算法[J]. 南京大学学报（自然科学版）， 2016， 52（4）： 693-704. （CAI Y P， YANG M. A multi-label feature selection algorithm by exploiting label correlations locally[J]. Journal of Nanjing University （Natural Science Edition）， 2016， 52（4）： 693-704.）

[19] 杨明， 蔡亚萍. 一种结合标记相关性的半监督多标记特征选择及分类方法： CN201610256462.9[P]. 2016-09-28[2019-01-10]. （YANG M， CAI Y P. A semi-supervised multi-label feature selection and classification method combined with marker correlation： CN201610256462.9[P]. 2016-09-28[2019-01-10].）

[20] BRAYTEE A， LIU W， CATCHPOOLE D R， et al. Multi-label feature selection using correlation information[C]// Proceedings of the 2017 ACM Conference on Information and Knowledge Management. New York： ACM， 2017： 1649-1656.

[21] LIU L， ZHANG J， LI P， et al. A label correlation based weighting feature selection approach for multi-label data[C]// Proceedings of the 2016 International Conference on Web-Age Information Management， LNCS 9659. Cham： Springer， 2016： 369-379.

[22] SPOLAR N， MONARD M C， TSOUMAKAS G. A systematic review of multi-label feature selection and a new method based on label construction[J]. Neurocomputing， 2016， 180： 3-15.

[23] SHANNON C E. A mathematical theory of communication[J]. Bell System Technical Journal， 1948， 27（4）： 623-656.

[24] ZHANG M， ZHOU Z. ML-KNN： a lazy learning approach to multi-label learning[J]. Pattern Recognition， 2007， 40（7）： 2038-2048.

[25] ZHANG M， PEA J M， ROBLES V. Feature selection for multi-label naive Bayes classification[J]. Information Sciences， 2009， 179（19）： 3218-3229.

[26] ZHANG Y， ZHOU Z H. Multi-label dimensionality reduction via dependence maximization[C]//  Proceedings of the 23rd National Conference on Artificial Intelligence. Menlo Park， CA： AAAI Press， 2008， 3： 1503-1505.

[27] LIM H， LEE J， KIM D. Optimization approach for feature selection in multi-label classification[J]. Pattern Recognition Letters， 2017， 89： 25-30.