基于拉普拉斯分值和鲸鱼寻优SVM的滚动轴承故障诊断

白丽丽，韩振南，任家骏，秦晓峰

(太原理工大学 机械与运载工程学院，太原 030024)

滚动轴承作为旋转机械系统中的关键部件，对其故障诊断技术的研究具有重要的现实意义[1]。而故障诊断技术的核心是对该部件进行模式识别，过程包括特征提取、特征选择和分类识别[2-4]。在机械系统运转的过程中，可以通过分析采集到的信号得到一些包含了滚动轴承运行状态的信息，这些信息构成了表征滚动轴承运行状态的特征集。由于不同特征的灵敏度不同，因此它所表征的故障信息量也是不同的[5]。特征太多会造成特征之间的冗余性，故需要对特征集进行特征选择，选用数量较少的且较敏感的特征来准确的表征滚动轴承的运行状态。

目前，常用的特征选择方法为费舍尔分值法(fishes score,FS)[6]和拉普拉斯分值法(laplace score,LS)[7]。FS更注重有类别信息的特征，而忽略了保留特征的局部信息。作为一种无监督的特征选择方法，LS结合了特征的局部保留能力，同时使用方差值来表征包含信息的能力。LS可以从原始特征集中有效地选取包含故障信息的特征,不仅可以避免维数灾难，而且可以改进滚动轴承故障识别的表现。

在特征选择之后，有必要引入支持向量机(support vector machine,SVM)来进行故障的自动识别。SVM是以统计学习为理论进行小样本分类和预测的机器学习算法，但是SVM参数的选择严重影响最终的识别效果[8]。由于参数选取的不同，同样的训练样本建立的模型也会产生较大的差别，最后的识别精度也会有较大的差异。本文将一种新型的元启发式智能仿生算法——鲸鱼优化算法[9-11]用于寻找SVM的最佳参数，即基于鲸鱼算法寻优的支持向量机(support vector machine optimized by whale algorithms，WOASVM)。

本文是基于LS和WOASVM方法对滚动轴承进行故障诊断的研究。首先，形成一个包含时域、频域以及时频域中若干特征的特征集，然后计算其LS值，并按其值的大小排序，选择一些特征形成特征向量。接着使用鲸鱼算法来寻找SVM中最佳的惩罚因子和核参数。最后，利用WOASVM来进行滚动轴承的故障状态识别。

1 故障特征提取

当机械设备产生故障时，时域信号的幅值和分布由于脉冲或振动的产生而改变。所以从时域波形中提取的时域统计特征参数可以最直观、最简便的反映机械系统的故障。本文选择波形指标、峭度指标、峰值指标、裕度指标和脉冲指标作为时域特征参数，依次标记为特征1-5.

如果发生故障，一些异常频率成分可以反映机器的运行状况。所以，在频域提取一些指标对故障诊断至关重要。本文选取了频率均值、频率方差、标准偏差频率、均方根频率和重心频率作为频域特征参数，依次标记为特征6-10.

时频域特征具有良好的聚合性和直观性，可以同时反映信号的时域和频域特性，因此，有效提取时频特征参数对于故障诊断的准确性有着至关重要的意义。本文选取了更加完善的完整自适应噪声集成经验模态分解方法(complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN)，将信号通过CEEMDAN分解后，取前5个本征模态函数的相对能量特征作为时频特征参数(标记为特征11-15)来监控滚动轴承的健康状况。

因此，本文从时域、频域、时频域3个角度，共选取了15个特征，形成一个原始的特征集来表征滚动轴承的运行状态。

2 拉普拉斯分值特征选择

特征维数的增加将导致很大的计算负担并降低计算的效率。因此，为了提高故障诊断的效率和有效性，通常需要进行特征选择来消除冗余信息，以提高分类的性能。

拉普拉斯分值是一种基于拉普拉斯特征映射(laplacian eigenmaps,LE)和保局投影(locality preserving projection,LPP)的有效的特征选择方法[12]。其基本思想是：采用样本的局部特征来衡量特征，对于特征空间中的两个样本，它们的距离越小，则属于同类的概率就越高[13]。LS算法步骤描述如下：

1) 使用给定的m个数据样本点构造近邻图G.如果数据点xi和xj足够接近，则认为样本i和样本j之间有边连接；否则，认为样本i和样本j没有边连接。

2) 定义权重矩阵S，如果i和j是连通的，则Sij如式(1)定义，否则Sij=0.

(1)

式中，t是一个常量。S是对数据空间的局部结构建模，用于测量两个样本点的相似性，同时也描述了数据空间的固有局部几何结构。

3) 定义fr=(fr1,fr2,…,frm)T，I=(1,1,…,1)T，D=diag(SI)，L=D-S.其中，fri代表了第i个样本的第r个特征；I表示m维的单位向量；矩阵L为拉普拉斯矩阵。为了避免某些维数据之间的差异很大而支配近邻图的构造，对每个特征去均值处理，如下：

(2)

4) 第r个特征的拉普拉斯分值Lr计算如下：

(3)

式中，Var(fr)为第r个特征的估计方差。将这些特征按照LS从低到高排序，最重要的特征排名在最前面。

3 鲸鱼算法优化的支持向量机

3.1 支持向量机

支持向量机 (support vector machine,SVM)的计算原理简单描述如下[14]。

将输入空间中线性不可分离的训练样本映射到新空间，转换为线性可分的数据加以分类。对于分类问题，SVM成为以下双重优化问题：

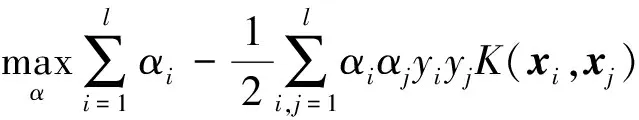
(4)

式中：α是对应的拉格朗日乘数；C为惩罚参数。

3.2 鲸鱼优化算法

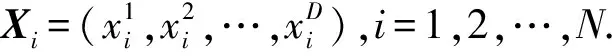
1) 包围猎物。鲸鱼可以确定猎物位置并包围它们。在WOA算法中，假设当前群体中的最佳位置是猎物，并且种群中的其他个体均向着最佳位置移动。使用式(5)更新位置：

X(t+1)=Xp(t)-A·|C·Xp(t)-X(t)| .

(5)

A=2ar1-a.

(6)

C=2r2.

(7)

式中：r1和r2是[0，1]之间的随机数；α称为收敛因子。

2) 泡网攻击。收缩包围机制：随着收敛因子α的减小，用公式(5)实现了收缩包围机构。螺旋更新位置：使用以下公式(8)模拟鲸鱼捕捉猎物的螺旋运动：

X(t+1)=D′eblcos(2πl)+Xp(t) .

(8)

式中：D′=|Xp(t)-X(t)|代表猎物与第i条鲸鱼之间的距离；b定义了对数螺旋形状，l为[-1，1]的随机数。鲸鱼不仅在猎物的收缩环周围游动，而且沿着螺旋路径运动。

3) 搜寻猎物。鲸鱼可以根据彼此的位置随机进行搜索：

X(t+1)=Xrand(t)-A·|C·Xrand(t)-X(t)| .

(9)

式中，Xrand是随机选择的鲸鱼的位置向量。

鲸鱼优化算法(WOA)的流程图如图1所示。

图1 鲸鱼优化算法(WOA)流程图Fig.1 Flowchart of the WOA

4 故障诊断流程

基于LS和WOASVM的滚动轴承故障诊断的流程图如图2所示，其具体步骤如下：

1) 将原始振动信号分类，分别提取各个类别中前文介绍的时域、频域和时频域的特征，形成一个15维的初始特征集。

2) 将初始特征集按照LS值从小到大的顺序排序，并选择前若干个特征形成特征矩阵。

3) 将新的特征矩阵中的前60个样本作为训练样本，后90个样本用于测试。

4) 设置WOA的初始化参数，计算相应的适应度函数，得到最优的惩罚因子和核参数的值。这里所使用的适应度函数与粒子群寻优所使用的适应度函数类似，设定为搜索到的惩罚因子和核函数代入SVM训练后得到的识别精度。最优的惩罚因子和核函数的值，最终可得到最优的识别精度。

5) 使用得到的最优参数进行训练，然后对测试样本的特征矩阵进行诊断，从而实现对滚动轴承故障的诊断。

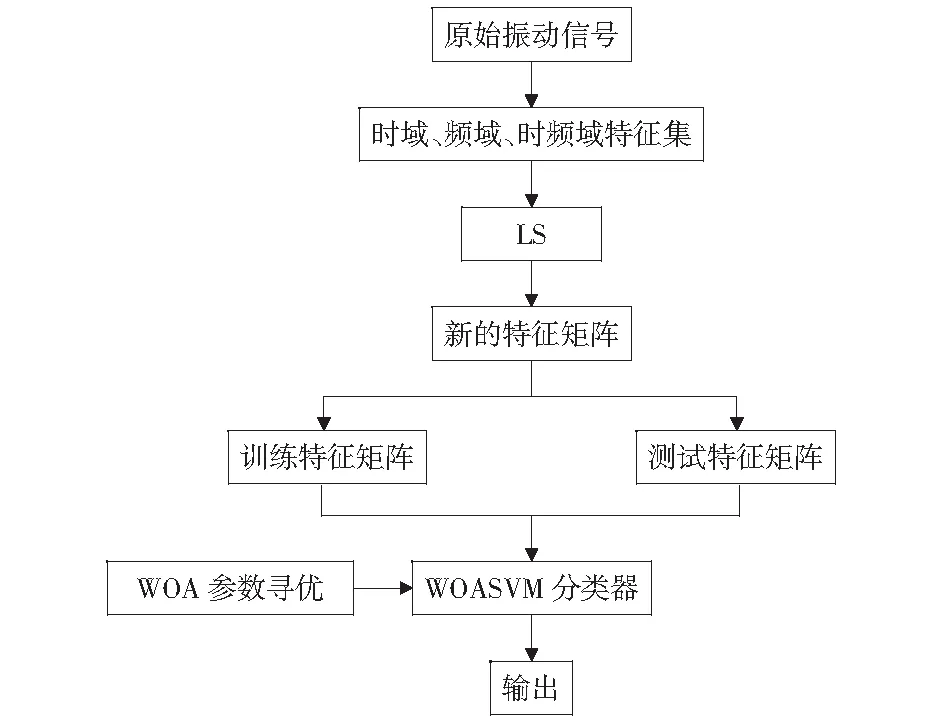
图2 故障诊断流程图Fig.2 Flow chart of the fault diagnosis

5 应用实例

5.1 实验数据验证

本文利用Case Western Reserve University提供的滚动轴承试验数据[16]进行了研究。使用的轴承为6205-2RS深沟球轴承，直径为0.177～0.533 mm的单点故障是通过电火花加工的。使用正常滚动轴承、滚动体故障、外滚道故障和内滚道故障4种故障类型的试验数据。在本文中，使用转速1 797 r/min、采样频率12 kHz的驱动端轴承数据。数据的详细分类信息如表1所示。

将以上10组类别的每一类分类类别中各取150个样本，得到1 500个样本。将这1 500个样本分别提取前文所述的时域、频域和时频域特征，共15个，形成一个1 500×15的初始矩阵。

然后LS用于对初始特征进行排序，根据LS新的特征顺序从低到高为：11，7，10，9，6，13，2，3，1，8，4，5，12，15，14.可以看出使用LS方法后，特征顺序完全打乱。其中通过CEEMDAN分解后的第一个本征模态函数的相对能量特征最为重要，包含的信息最多。

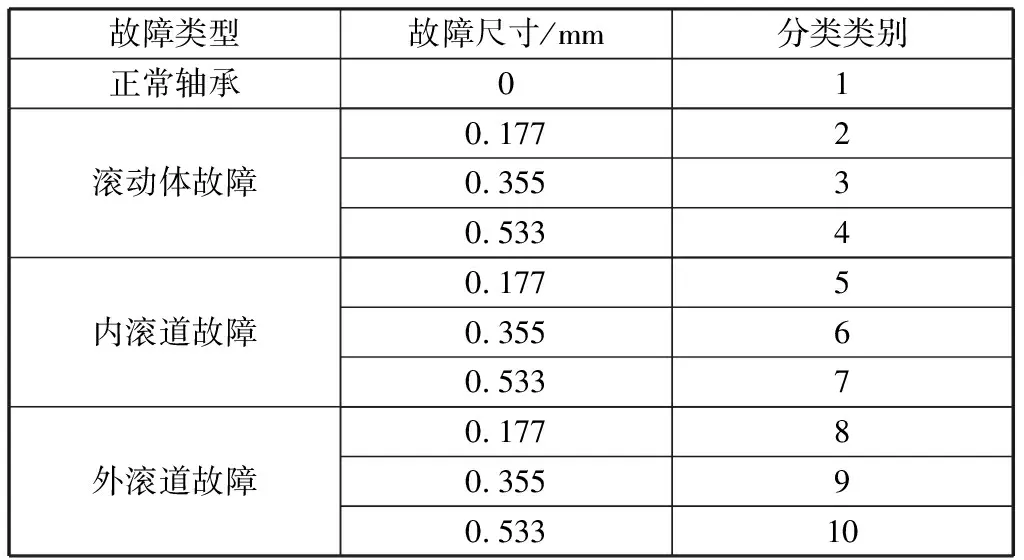
表1 滚动轴承的详细分类信息Table 1 Detailed classification information of the rolling bearing

取LS顺序中的前3个特征元素作散点图，如图3，可以直观地看出，前3个特征元素已经可以将滚动轴承的故障类型完全区分开，甚至故障的严重程度也在一定程度上得到了分离。说明LS选择的特征可以表征最多的故障信息。

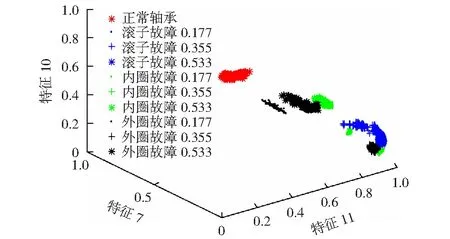
图3 前三个特征元素形成的散点图Fig.3 Scatter plot of the three feature elements

选取LS选择后的前5个特征元素，将每组中的前60个样本输入WOASVM进行训练，其余用于测试。设定WOA算法的鲸鱼种群数目为30，最大迭代次数为100.通过WOA寻找到的最佳惩罚因子为0.633 5，最佳核函数为60.401 1.利用这些参数对测试样本进行测试，可得到如图4的结果。由图可以看出，测试集的识别率达到了98%.

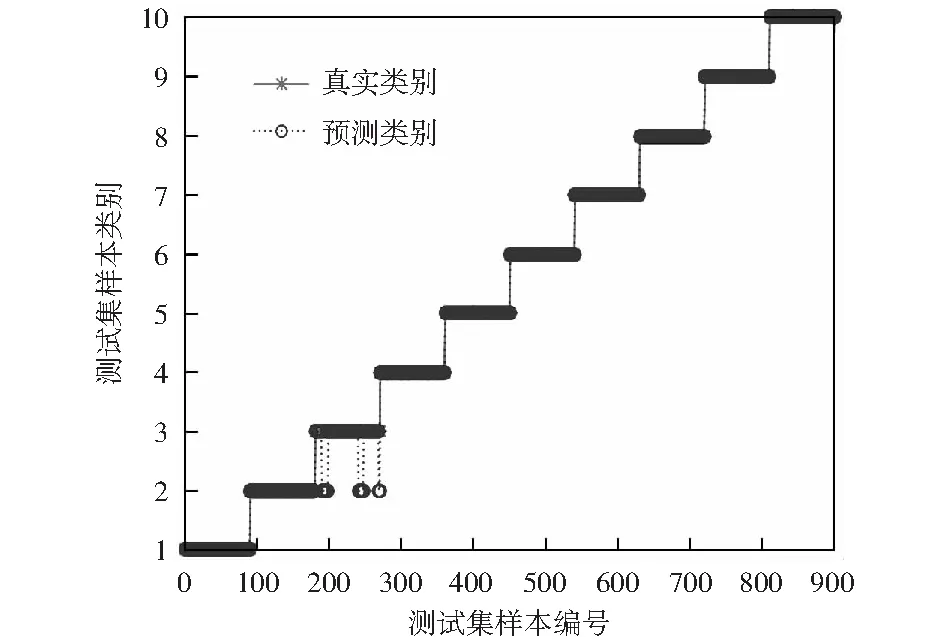
图4 使用所提出的方法后测试样本的输出Fig.4 Outputs of testing samples by using the proposed method

为了进一步验证所选出的特征数的影响，用选择出的不同数目的敏感特征来进行测试，可以得到，前1个特征的识别率为70.56%，使用前3个特征的识别率可达到95.44%， LS重新排序后的前5-6个特征，识别率就可以达到98%左右。之后特征数目越多，识别率反而越低，最终前15个特征的识别率仅能达到89.33%.这是因为，有些特征对滚动轴承的缺陷并不敏感，而特征太多反而使得故障信息产生了冗余，甚至干涉到了敏感信息对于相关故障的分类。所以通过LS对特征进行选择不仅降低了特征太多所产生的计算代价，而且提高了分类精度，更加准确地识别出故障的类型及严重程度。

通过对比来进一步验证本文所提出方法的有效性，应用常见的交叉验证法、网格搜索法、遗传算法、粒子群算法和鲸鱼算法分别对SVM的惩罚因子和核参数进行寻优。同时对这几种方法的初始参数值设置进行了统一，即种群大小设为30，迭代次数为300，搜索空间为[0.1,100]和[0.01,1 000].同样使用上文通过LS选择后的前5个特征进行训练、测试，每组实验进行10组，取其识别率和运行时间的平均值。具体的分类识别率和运行时间见表2.

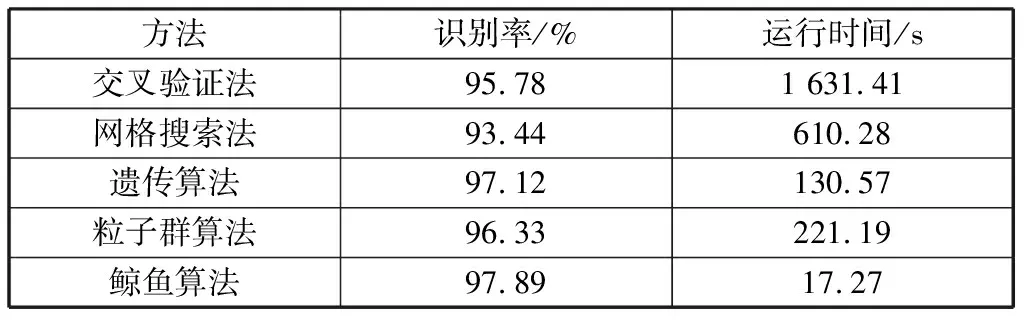
表2 不同寻优算法对SVM的影响Table 2 Influence of different optimization methods on SVM

从表2可知，所有经过寻优算法优化后的SVM都得到了不错的识别率。交叉验证和网格搜索法的识别率是这其中较低的，且交叉验证法的运行时间特别长。启发式算法，如遗传算法、粒子群算法得到的识别率都比较高，但这两者的运行时间都较长。而鲸鱼算法不仅得到了很高的识别率，耗时也是最短的。

5.2 自建试验台数据验证

本文自建试验台的实物图如图5所示。试验的轴承在试验齿轮箱中，为2612圆柱滚子轴承，采用转速为1 420 r/min、采样频率为2 000 Hz的4种状态下轻载和重载时的振动信号。其中故障为宽度0.3 mm的划痕，轻载和重载表现为扭矩的不同，其详细的分类情况参见表3.

图5 自建试验平台的实物图Fig.5 Physical chart of self-built test platform

故障类型故障尺寸/mm加载情况分类类别正常轴承0轻载0重载1外圈故障0.5轻载0.5重载2滚动体故障0.7轻载0.7重载3内圈故障0.3轻载0.3重载4

将每组故障类型同样分别取150个样本且提取时域、频域和时频域的15个特征，形成1 200×15的初始矩阵。计算LS，得到新的特征排序为：8，7，10，11，14，6，9，3，2，4，1，12，13，15，5.通过LS选择后将前3个特征元素做散点图在图6中显示，可以看出每一类的分类类别基本上可以各自聚在一起，滚子故障与其余故障状态分离明显，其余的故障状态基本上可以分离，但交汇处有些干涉。但这只是前3个特征元素所表现的分离效果，选取前若干个特征元素输入SVM后，可以得到准确的分类精度的数值。

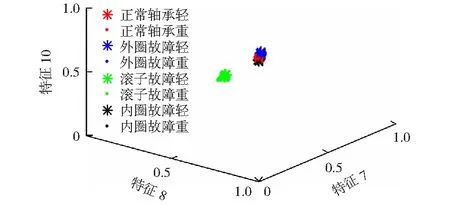
图6 前三个特征元素形成的散点图Fig.6 Scatter plot of the three feature elements

在状态识别过程中，选取的特征数过多会造成计算量过大，选取的特征数过少，又无法全面的表征故障状态。使用不同数目的敏感特征来表征滚动轴承的故障状态，同样运行10次，去平均的故障识别率，具体结果见图7.由图可以看出，随着选择的特征数目的增加，识别率不总是增长的，特征数目在5-7，11-14范围内的识别率总体较高，为后续选择合适的敏感特征数目提供了参考。

图7 不同数目的特征的识别率Fig.7 Recognition rate of different numbers of features

由上，本文选择前5个特征形成敏感特征矩阵来进行分类识别。同样选取60个样本训练，其余90个样本测试，输入WOA优化的SVM中，得到了99.31%的识别精度(最佳惩罚因子为11.13，最佳核参数为86.99)，运行时间仅为3.41 s.再一次证实了本文所提方法的有效性与高效性。

6 结论

本文提出了一种基于LS和WOASVM的滚动轴承故障诊断算法。首先，将原始振动信号时域、频域和时频域中的一些特征参数运用LS进行特征排序，选择敏感特征形成特征矩阵，并将形成的特征矩阵进行模式识别。接着，通过鲸鱼算法对SVM进行参数寻优，通过WOASVM得到最终的识别结果。该方法利用LS方法的保局能力来衡量特征，从而可以有效地选择出包含故障信息较多的特征，同时减少冗余特征，提高故障识别率。同时利用鲸鱼算法优化SVM的参数，构造出最优的故障模式识别分类器，使得其收敛速度和精度均优于其他优化算法。通过实验和对比结果表明本文所提出的方法能够有效地实现滚动轴承故障类型和故障严重程度的诊断。本文提出的方法简单有效，可以为机械传动系统的智能故障诊断提供新的参考。