薄柔H型钢柱抗侧向冲击性能研究

路国运，陈鹏程

(太原理工大学 土木工程学院，太原 030024)

根据力学性能的不同，在以截面分类为基础的钢结构设计规范中，不同截面类别的构件对应着不同的设计准则[1-3]。薄柔截面构件是指不满足钢结构构件截面分类准则中塑性截面要求的板件组成的大宽厚比截面构件。当单位长度质量一定时，相对于普通截面钢构件，薄柔截面钢构件截面形状经济合理，且具有更大的弹性抗弯刚度及屈服弯矩，更满足钢结构节材、节能和环境友好的特点。随着我国城镇化的不断发展，近年来多层钢结构在国内逐步推广，H型钢作为梁柱构件的支撑，其结构稳定性高，适用于承受振动和冲击荷载大的建筑结构，抗自然灾害能力强，特别适用于一些多地震发生带的建筑结构以及桥梁、船舶、起重运输机械、设备基础等[4-5]。据统计，在世界上发生7级以上毁灭性大地震灾害中，以H型钢为主的钢结构建筑受害程度最小[6]。而薄柔H型钢由于其轻质高强的特点被广泛应用于量大面广的住宅、低多层办公楼等民用与公共建筑上[7-10]，在国内建筑行业内引起高度关注。

然而，工程结构在服役期限内不可避免地会遭受意外的爆炸[11]、滚石冲击[12-13]、车辆碰撞[14-16]等极端冲击荷载作用，在进行结构设计时需要考虑这些极端荷载的影响。因此，对冲击荷载下结构构件的动力性能进行研究，进一步对结构进行合理化设计，以提高结构抗连续倒塌能力就显得尤为重要。

针对H型钢柱抗侧向冲击研究，AL-THAIRY et al[17]建立了轴向压力下钢柱受侧向撞击的有限元模型并与前人实验结果对比，验证了模型的有效性。利用该模型进行参数分析，研究冲击位置、冲击质量、设计轴力对H型钢柱破坏失效模式的影响。MAKAREM et al[18]利用新的钢材本构VA[19]建立了轴向压力下HY-100高强H型钢柱受侧向撞击的有限元模型，研究了冲击速度、冲击位置、冲击质量及预加轴力对高强H型钢柱局部破坏的影响。WANG et al[20]利用ANSYS/LS-DYNA建立了钢梁、梁柱连接受横向冲击的有限元模型来模拟钢梁、梁柱连接受意外冲击荷载的撞击，并通过落锤实验验证了模型的有效性。在此基础上，设计了6组有限元模拟工况讨论冲击能量、冲击位置、材料强度、连接板厚度等对H型钢梁、梁柱连接抗冲击性能的影响。

由上可知，关于H型构件抗侧向冲击研究，其截面形式主要以普通截面为主，但针对薄柔H型构件的抗冲击性能研究相对较少。因此，本文对冲击荷载作用下薄柔H型钢构件的动态力学性能进行了研究，为薄柔构件抵抗冲击荷载作用及倒塌提供更为合理的设计建议，有效提高其在建筑中的应用效率，为加速我国钢结构产业化发展及建设做出贡献。

1 有限元模型建立与校核

1.1 模型建立

采用H型截面钢构件在两个方向上的尺寸远大于第三个方向，建模时单元类型选用四节点减缩积分格式的三维壳单元(S4R)，有限元模型对实验结果进行相互校验时，材料强度取钢材拉伸实验实测值。采用有限元模型进行参数化分析时，材料模型采用三折线模型，如图1所示，其中屈服强度取fy=345 MPa，极限强度fu=500 MPa，弹性模量E=2.06×105MPa，强化段切线模量取Eh=E/100=2.06×103MPa，泊松比0.3.落锤采用实体建模，由于冲击过程中落锤变形很小，且轻微变形对计算结果影响很小，所以将其约束为刚体，网格采取扫略划分，单元选取八节点减缩积分格式的三维实体单元(C3D8R)。为了保证计算精度，对着重分析的关键部位做网格加密处理。

图1 钢材材料模型Fig.1 Stress-strain curve of steel used in parametric study

边界条件为一端固支，一端滑动，为了实现构件底端固接的边界条件，采用动态耦合(Kinematic coupling)将柱底截面的所有节点耦合在RP-1上，然后约束 RP-1的所有自由度，这样不但实现了柱底截面的固接，也保证了大变形后，柱底截面依然能够保持原截面。在柱顶截面，通过刚体(Rigid body)将柱顶截面转化成一个刚面，以防止应力集中导致的板件压溃，然后将柱顶截面所有节点的自由度赋予RP-2上，约束RP-2除轴向外所有的位移和转角，即实现了加载端滑动的边界条件。构件模型如图2所示。

图2 有限元网格模型Fig.2 Mesh of finite element model

由于应变率对钢材的屈服强度有显著影响，而C-S本构模型由于概念明确，形式简单，在船舶领域和钢结构抗冲击荷载领域也有较多应用[21-24]。因此，本文模拟选用考虑应变率效应的Cowper-Symonds力学模型，具体表达式如下：

(1)

为真实地模拟柱受侧向冲击荷载下的动态响应，需在钢柱受冲击荷载之前进行轴力的施加，并在冲击过程中保持轴力的稳定。因此，将分析设置为两步：第一步在构件轴向施加轴力，利用ABAQUS中的平滑分析步幅值曲线(Smooth step)在单独的分析步骤中施加轴向荷载，并保证足够的加载时间，减少惯性效应的影响；第二步在柱达到平衡后在冲击部位通过定义初始速度实现冲击载荷的加载。冲击物与柱之间的接触定义为无摩擦的面-面接触，使用动力学接触方法。

1.2 模型校核

由于薄柔H型截面钢柱的冲击实验较少，为保证有限元模型的精确性，本文利用霍静思[26]的各组普通H型截面钢梁冲击实验进行验证，这里选取部分结果来进行说明。图3为冲击力、位移时程曲线对比，图4为试件HR43局部变形对比图，表1为主要数据对比包括冲击力峰值(Fmax)、平台值(Fstable)及跨中最大位移(dmax)，可以看出，有限元结果与实验结果吻合较好。

图4为工况HR43试件的跨中局部变形的实验和模拟对比图。可以看出局部变形主要集中在靠近加劲肋两侧，上翼缘加强板两侧应力较大，钢梁板件保持完好，未发生撕裂破坏。数值模拟结果与实验结果基本吻合。

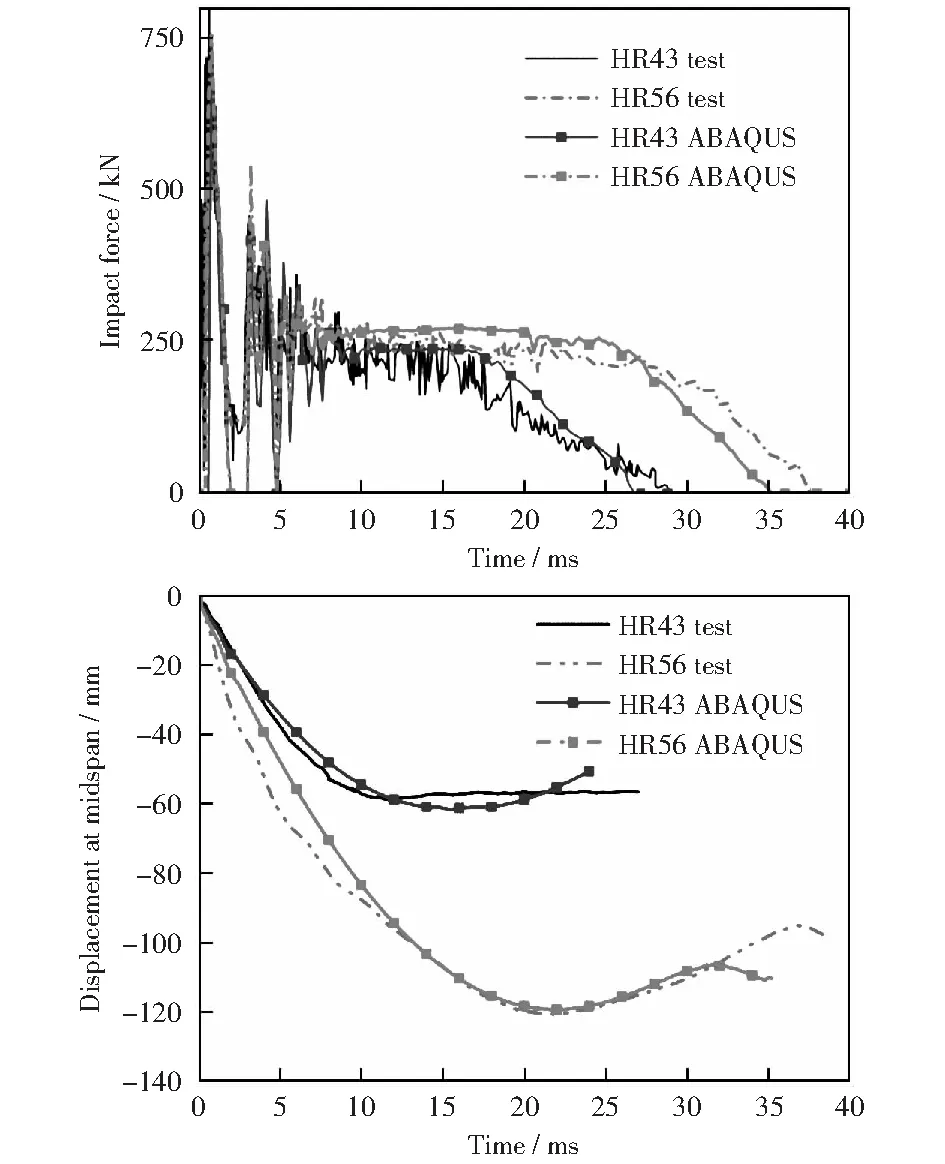
图3 冲击力、位移时程曲线对比Fig.3 Comparision of impact force and displacement between numerical and test data

图4 HR43局部变形对比Fig.4 Comparision of local deformation mode between experimental and numerical

表1 主要数据对比Table 1 Comparision between numerical and test data

综上可知，根据1.1节的方法建立的有限元几何模型及采用的材料模型、单元类型、接触算法、计算控制方法等较为合理，能够较为准确地模拟H型截面钢构件在冲击作用下的破坏过程。

2 参数化分析

2.1 试件选取

试件尺寸：h×b×tw×tf=350 mm×240 mm×8 mm×10 mm，有效长度L=3 000 mm，冲击部位位于试件柱中。冲击质量m=1 t.撞击物截面为矩形，尺寸为360 mm×100 mm.整体模型总单元数为15 868.所选构件符合实际工程应用，且满足各国规范的薄柔截面规定。

2.2 参数设置

本节对影响构件在冲击荷载下力学性能的主要因素，如冲击速度、冲击质量、冲击位置、轴压力等展开详细研究。表2为构件的荷载参数设置。其中，第一组：T1，T2，T3，冲击速度与冲击质量都在变化，但总冲击能量不变；第二组：T4，T5，T6，冲击质量变化，其他参数不变；第三组：T6，T7，T8，冲击速度变化，其他参数不变；第四组：T6，T9，T10，冲击位置变化，其他参数不变；第五组：T6，T11，T12，T13，T14，轴力变化，其他参数不变。

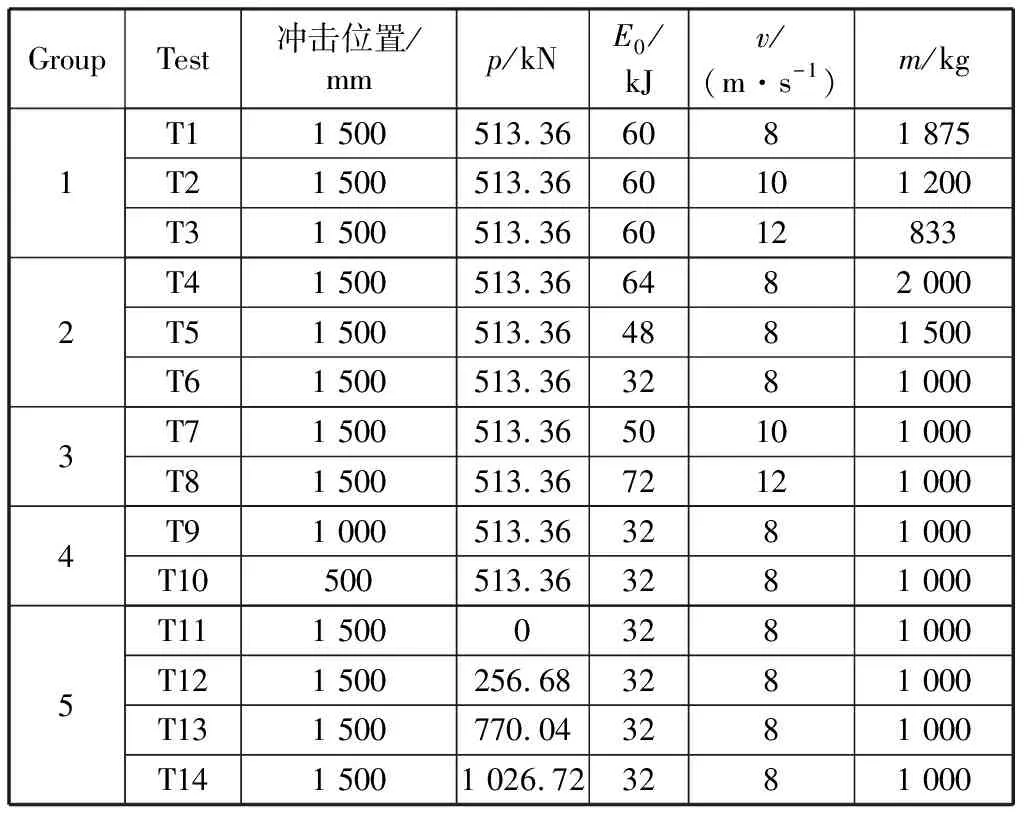
表2 荷载参数设置Table 2 Parameters of load

将模拟得到的主要结果列于表3中。

表3 数值模拟主要结果Table 3 Schedule of numerical simulation

2.3 不同速度与质量对构件的影响

图5为相同冲击能量，不同冲击质量与速度的组合对构件抗冲击性能的影响。可以看出，冲击质量对于构件受冲击作用的时间有明显影响，质量越大，冲击作用时间越长。冲击质量对撞击处位移的影响大于冲击速度。此外，可以看出，在冲击能量一定的情况下，不同冲击质量与速度的组合对构件的耗能及耗能率影响不大，这是由于构件的耗能主要是由初始冲击能量决定的。

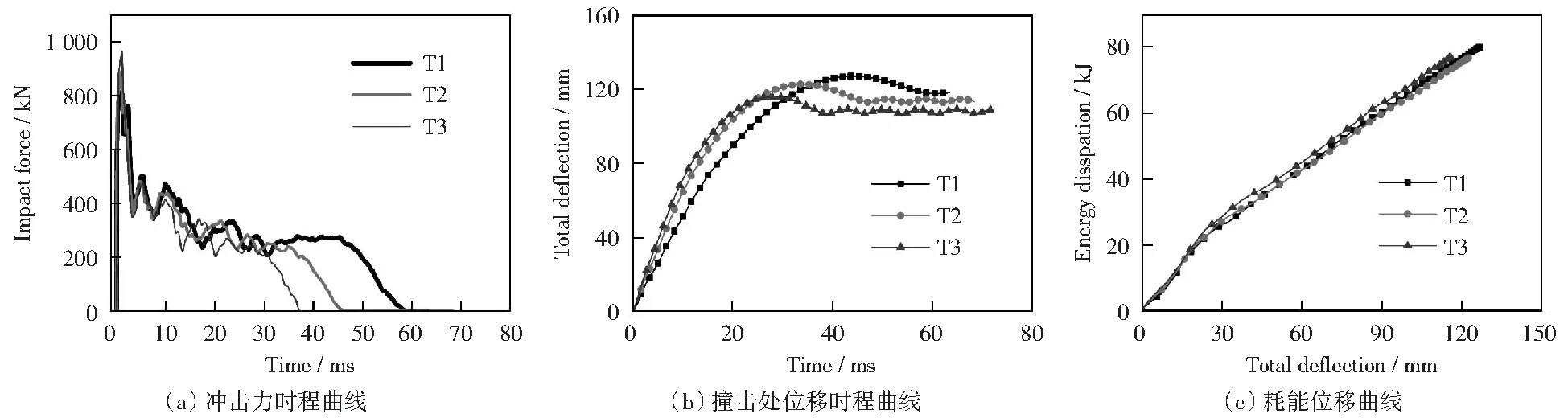
图5 不同的冲击质量与速度对构件抗冲击性能的影响Fig.5 Effect of identical impact energy but different mass and velocity on impact resistance of members

2.4 冲击速度对构件的影响

保持冲击质量不变，通过改变初始冲击速度来实现冲击能量的变化。图6为冲击速度对H型钢构件动态力学性能的影响，可以看出，随着冲击速度的提高，构件冲力峰值增大，冲击力平台值提高，且冲击时间也有所增加，撞击处位移显著增大。这是由于随着冲击能量的增大，构件需要产生更大的塑性变形来消耗能量。还可以看出，随着冲击速度的增大，构件的耗能及单位位移下的耗能在增大，这是由于构件变形速度增大使得材料应变率上升，因而材料强度提高，从而表现出截面抗弯强度的增大。

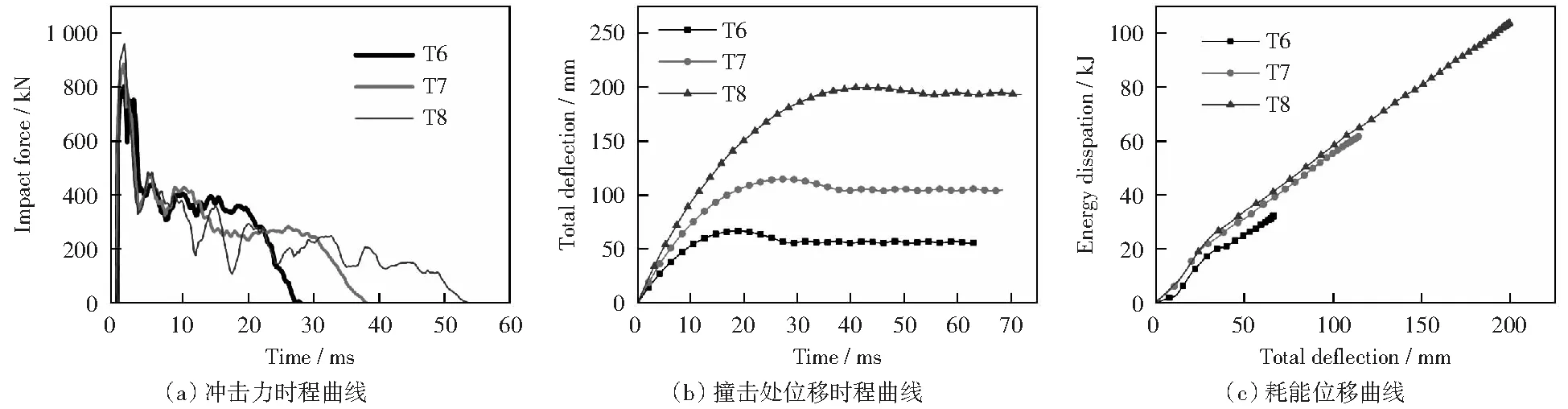
图6 冲击速度对构件抗冲击性能的影响Fig.6 Effect of impact velocity on impact resistance of members

2.5 冲击质量的影响

图7为冲击质量对构件抗冲击力学性能的影响，随着冲击质量的增大，冲击力峰值增长较小，冲击质量由1 000 kg增长到2 000 kg，增长100%，冲击力峰值增长1.4%；但平台值有所降低，冲击持时变长，增长126.5%，说明冲击质量对构件的冲击持时影响较为明显。冲击物质量的增大使得构件撞击处的位移增大，撞击过程中构件的变形速度也有了一定的增大。还可以看出，随着冲击质量的增大，构件消耗能量增大，但单位位移下的耗能几乎不变。

结合图5至7可得，最大冲击力主要由冲击速度决定；质量相同的条件下，速度越大，最大冲击力越大；相同冲击速度下，冲击质量越大，冲击时间越长；但落锤质量对最大冲击力的影响不是很明显；相比最大冲击力，冲击质量对冲击时间影响较大；冲击能量的增加导致钢构件耗能的增加。

图7 冲击质量对构件抗冲击性能的影响Fig.7 Effect of impact mass on impact resistance of members

另外，通过对比可以发现速度对钢构件单位位移下的耗能影响要大于质量。这可能是因为速度的增加导致了应变率的增加，使得钢材的屈服强度提高，进而单位位移耗能提高。

2.6 冲击位置对构件的影响

冲击位置对构件动态力学性能的影响如图8所示。可以看出，随着冲击部位远离柱中，冲击力平台值有所提高，但幅度不明显，冲击时间缩短，而当冲击位置距离柱底1 000 mm时，冲击部位的位移最大，构件耗能最多。因此，距柱底1/3处受到冲击被认为是柱的抗弯能力最差的情况，表明该边界条件下，距柱底1/3处是构件遭受冲击的最不利部位。

图8 冲击位置的影响Fig.8 Effect of impact location on impact resistance of members

2.7 轴压力的影响

构件在不同轴压力下的冲击力时程曲线和撞击处位移时程曲线如图9所示。从图9及表3中可以看出，在峰值阶段，轴力对构件冲击力峰值形状及峰值大小影响较小；对构件撞击处的侧向变形影响也较小，因此在峰值阶段，轴力对构件的耗能影响较小。在冲击力平台段，当n=0.1，0.2时，相比于n=0构件，平台持续时间与冲击力平台值变化不大；当n增大至0.3时，可以看出，冲击平台持续时间较n=0.1，0.2也有所上升；同时，冲击力平台值有明显降低，说明轴力对构件的侧向刚度有了一定影响。当n=0.4时，可以看出，冲击力平台值显著降低，冲击持续时间显著增大。还可以看出，随着轴力增大，构件撞击处的侧向变形持续增大，这是由于轴力的增大使得构件的侧向刚度减弱，而构件变形速度基本不变，说明轴力对构件撞击处的侧向变形速度影响较小。另外，随着轴力增大，构件的耗能逐渐增大，单位位移下的耗能逐渐增大，且轴力对构件耗能的影响主要在冲击力平台阶段。

图9 轴压力对构件抗冲击性能的影响Fig.9 Effect of impact location on impact resistance of members

3 结论

一端固定一端滑动H型钢柱在柱中受冲击荷载作用下的变形模式为：整体弯曲变形与局部变形的耦合，在柱中部位形成塑性铰，冲击部位是构件塑性变形的主要发展部位。钢柱的冲击处局部变形主要表现为：柱中加载区上翼缘有明显的下凹，腹板产生面外变形，随着变形的发展，在靠近边界处的柱顶和柱底部分产生了明显的压曲变形。

冲击能量的增加导致钢构件塑性耗能的增加，最大冲击力主要由冲击速度决定；质量相同的条件下，速度越大，最大冲击力越大；相同冲击速度下，冲击质量越大，冲击时间越长，但冲击质量对最大冲击力的影响不是很明显；相比最大冲击力，冲击质量对冲击时间影响较大。

由于速度的增加导致材料应变率的增加，使得钢材的屈服强度提高，因此速度使得钢构件塑性耗能率提高。相比之下，冲击质量并不能改变其塑性耗能率。

轴压比对构件在侧向冲击下的力学性能有较大影响，随着轴压比的增大，构件冲击力降低，撞击处位移增大；另外，随着轴力增大，构件的耗能逐渐增大，耗能率逐渐增大，且轴力对构件耗能的影响主要在冲击力平台阶段。