《信号与系统》课程“采样定理”的课堂教学设计

张亚周 孙雪丽 钟兆根

【摘 要】采样定理是《信号与系统》课程的重点内容之一。并且由于其理论比较复杂且抽象难以理解，因此也是本课程课堂教学的一个难点。本文通过对采样定理的理论解析，以“提出问题-分析问题-解决问题-深化理解”为主线，综合采用多种教学方法进行课堂教学设计，取得较好的教学效果。

【关键词】信号与系统;采样定理;问题式教学法

【中图分类号】G642.0       【文献标识码】A

【文章编号】2095-3089（2019）24-0010-01

一、引言

信号与系统课程是我校电子信息类各专业的一门重要专业基础课，在专业课程体系中起着承前启后的作用。采样定理是该课程的重要知识点之一，并且在社会生产和日常生活中有着较为广泛地应用。特别是随着数字技术的发展，数字系统迅速得到普及。而我们通常遇到的信号大部分都是连续信号。采样定理则帮助我们在连续时间信号与离散时间信号之间架起了一座桥梁。可以说没有采样定理，就没有数字技术的现代化。

在传统的灌输式课堂教学模式中，往往是由教员首先介绍采样的概念，然后推导采样信号的频谱，最后给出结论。这样的教学模式使得学员就像是被牵着鼻子走，激不起学习兴趣和热情，最终导致大部分学员只是单纯机械地记住了结论，真正理解这个定理的学员却很少，更谈不上应用了。为了有效地增强学员对该采样定理的理解，提高课堂教学质量，本文基于问题式教学法对采样定理的课堂教学过程进行重新设计，以期让学员在问题驱动下，充分发挥学习的主动性，积极思考和探索，从而更加深入、透彻地理解和掌握采样定理的理论知识及应用技能。

二、课堂教学方法

本文提出在课堂教学中把教学内容问题化，遵循“提出问题—分析问题—解决问题—深化理解”的逻辑主线，以问题为导向，通过各问题相互承接，串起各部分教学内容，从而有助于学员循序渐进理解和掌握采样定理的理论知识。

1.提出问题：为什么要进行采样？

通过对这个问题的思考可以帮助学员们认识到采样的重要性和必要性，并且思考采样的目的和意义。在课堂教学过程中，笔者首先从学员熟悉的生活实例，比如手机、电脑、相机等常用设备入手，列举数字设备给我们社会生产和生活带来的巨大改变，来说明采样的重要性。然后以一段视频播放为例，让学员注意观察视频中的每一帧画面实际上都是一个离散的采样值，而当这些画面以不低于24帧/s的速度进行播放时，就构成了连续的图像。这同时也表明了连续信号是可以用离散时间信号来进行表示的[1]。

那么如何才能把连续系统离散化呢？在授课过程中，以一个学员熟悉的波形（比如正弦波）为例，引导学员思考要画出一个正弦波形，取多少点合适？离散点过于分散或紧密是否可行？为什么？从而引出问题：如何进行采样？学员都有以点画线的经验，这样做有助于学员较好地理解什么是采样。

2.分析问题：采样后信号在时域和频域如何变化？

在课堂讲授过程中，从时域和频域两个不同角度引出采样过程中所遇到的问题，以帮助学员理解采样带来信号的实质变化：

频域：（1）采样后信号的频谱是什么样的？与原信号频谱有何关系？

（2）在什么条件下，可以由采样信号的频谱恢复出原信号的频谱？

时域：（1）采样后的信号是否保留了原信号的全部信息？

（2）在什么条件下，可以无失真的恢复出原连续信号？

我们以理想采样为例，从时域和频域两个不同的视角分别进行分析。假设原连续时间信号为f（t），其傅里叶变换为F（jω），采样脉冲为p（t）=∑∞n=-∞δ（t-nTs），对应傅里叶变换P（jω）=ωs∑∞n=-∞δ（ω-nωs）。根据采样的定义可得：fs（t）=f（t）p（t），为减少数学推导，这里不直接求fs（t）的傅里叶变换，而是借助于频域卷积定理直接得出采样后的信号频谱

Fs=（jω）=12πF（jω）*P（jω）=1Ts∑∞n=-∞F[j（ω-nωs）]

这样一来就避免了复杂的数学推导，并且据此可得出结论：理想采样后信号的频谱是原连续信号频谱以为周期的周期延拓。

3.解决问题：采样定理。

虽然现在结论已经有了，但是如果直接通过理论分析两者之间的频谱关系，仍然存在一定的难度，而且学员对这种纯理论分析也感觉枯燥乏味。为此，笔者提出通过借助图形演示这种较为直观、形象的形式，来帮助学员理解频谱变化的具体过程，从而避开了理论分析的难点[2]，并进一步引出本次授课的重要知识点——采样定理。

首先，给出采样前信号的频谱，如图1（a）所示。根据此前的结论

引导学员自己动手画出采样后信号的频谱，如图1（b）所示。

想要无失真的恢复出原信号，必须得到原连续信号的完整频谱。结合上述图形，让学员思考：（1）要想得到原信号的完整频谱ωs，采样频率该如何选择？（2）对原信号的频谱有何要求？（3）在满足采样定理的条件下，如何由采样信号不失真的恢复连续信号，如何恢复？通过让学员直接从图形上分析它们之间的关系，可有效克服复杂的数学推导过程给学员造成的畏难情绪[3]。

至此，学员在教师的引导下，通过逻辑思维，利用已学过的知识和方法进行推导得出采样定理的知识内容，达到了预设目标。

4.深化理解。

为了帮助学员深刻理解采样定理，鉴于Matlab強大的计算能力和绘图能力，通过将MATLAB仿真引入课堂教学，把采样定理中比较抽象难懂的问题放在计算机界面上，直观清楚地观察信号的频谱及其搬移情况，可以帮助学员对所学的理论知识有更清楚、深刻的认识，提高学员学习兴趣并改善课堂教学的效果。

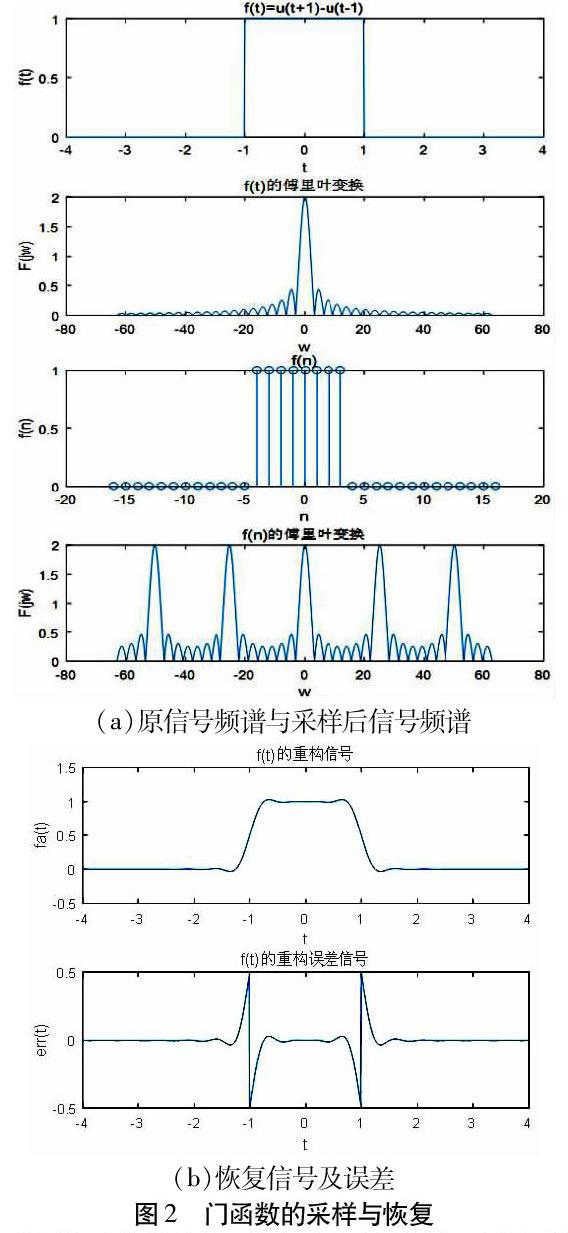
在授课过程中，我们以学员们熟悉的门函数为例进行仿真。首先，给出原信号的时域和频域波形，然后进行采样，给出采样后的时域和频域波形，如图2（a）所示。在讲解过程中可以随时改变采样频率，让学员观察在不同采样频率下恢复出的信号及恢复信号与原信号之间的误差，如图2（b）所示。从而可有效的帮助学员理解采样定理的内容。

此外，我们还以学员们比较熟悉的一段音乐作为原信号，不断降低采样频率来收听音乐效果，让学员直观感受不同采样频率下对信号的影响，从而有助于学员进一步加深对采样概念的理解。

三、结语

采样是数字信号处理的第一步，而采样定理为连续时间信号与离散时间信号的相互转换提供了理论依据[4]。作为《信号与系统》课堂教学的重要内容之一，如何加强学员对该部分理论知识的理解和掌握尤为关键。本文以“提出问题—分析问题—解决问题—深化理解”为主线，用问题串起全部教学内容。实践表明，这种教员引导下的问题式教学法极大地改变了传统“满堂灌”的模式，将学员由被动接受变为主动地参与。无论是学员的学习积极性，还是实际课堂教学效果，均得到了较为明显地提高。

参考文献

[1]曹路，甘俊英，应自炉，等.问题式教学法在《信号与系统》课程教学中的应用——以采样定理为例[J].湖北：长江大学学报（自科版），2015，12（25）：76-79.

[2]张玉珊，范海菊，杨育捷.基于“倒叙”的“采样定理”教学研究[J].北京：计算机教育，2015，5（9）：45-48.

[3]王怀兴.基于LabVIEW的采样定理仿真研究[J].湖北：湖北第二师范学院学报，2012，2（29）：30-32.

[4]邢国泉.采样定理的MATLAB实现[J].湖北：咸宁学院学报，2008，12（6）：39-47.

第一作者简介：张亚周（1979—），女（汉族），山东省平度市人，海军航空大学航空基础学院教师，讲师职称，硕士。研究方向：电子与通信系统工程。