气瓶液压试验进液量分析

危书涛

(1. 合肥通用机械研究院有限公司,安徽 合肥 230031； 2. 合肥通用机械研究院特种设备检验站有限公司,安徽 合肥 230031)

气瓶是用来储存高压气体的压力容器，在工业生产和人民生活中发挥着重要作用，由于其存在压力高、用量大和可移动性等特点，一旦发生泄漏或爆炸，对国民经济和人民生命财产将造成重大损失，因此对气瓶的质量控制较为严苛【1】。液压试验(一般用水作为液压介质，故通常称水压试验)是气瓶质量检验的重要环节，而液压试验进液量是表征气瓶整体结构塑韧性程度的重要指标。在气瓶液压试验和疲劳脉冲试验装置设计选型时，需要根据气瓶在试验压力下的实际进液量估算液压泵的流量和试验周期，方可保证设计制造出满足需求的试验装置【2】。气瓶液压试验进水量通常依靠液压试验机自带的测试系统，在气瓶液压试验过程中测量得到，增加了时间和经济成本。对于一些有特殊要求的气瓶，液压试验后残留的液压介质还会带来额外干扰。本文针对钢质气瓶，通过理论分析推导出气瓶液压试验进液量的计算公式，经实例试验分析，验证了理论计算公式的准确性，为直接、快速、精确地获取气瓶液压试验进液量提供了有效方法。

1 气瓶进液量的理论分析

液压试验过程中，气瓶由初始常压状态升压至液压试验压力，所需要的进液量容积包含两部分【3】：1)气瓶在内压作用下发生变形而引起体积膨胀所产生的形变增量容积；2)液压介质自身存在可压缩性，填充气瓶内容积的液体和加压过程中泵入的液体都会受内压作用而产生压缩变形，需泵入更多的介质进行补充，由此而产生的压缩量容积。对于气瓶而言，体积膨胀产生的形变增量可细分为直筒段形变增量和两端封头段形变增量。

1.1 气瓶直筒段形变增量容积【4-5】

气瓶直筒段内径为Di(mm)，长度为L(mm)。受压过程中，某一时刻直筒段瓶体轴向应变为εz(με)，环向应变为εt(με)，则此时直筒段瓶体内径和长度分别为：

(1)

直筒段形变增量容积ΔV(mL)为：

(2)

将式(1)代入式(2)，略去高次项，得到直筒段形变增量容积ΔV为：

(3)

1.2 气瓶两端封头段形变增量容积

气瓶通常由无缝管经旋压收口工艺制造而成，两端封头在旋压收口成形过程中会明显增厚【6】，而收口后封头最终形状通常类似于半球形、半椭球形或半尖球形，因此两端封头处的应力水平远低于直筒段，形变量极小。同时考虑到两端封头段长度占气瓶总长度的比例较小，故气瓶两端封头段的形变增量容积可以忽略不计。

1.3 液压介质的压缩量容积

液压试验时，气瓶内液压介质的压缩量为：

ΔVp=(V+ΔV)×p×βt

(4)

式中：ΔVp——压缩量，mL;

V——气瓶容积，mL;

p——试验压力，MPa；

βt——试验介质在试验压力和试验温度下的压缩系数。

由上述分析计算得到液压试验过程中气瓶进液量ΔVi(mL)与应变的关系为：

(5)

式(5)中直筒段瓶体轴向应变εz和环向应变εt可利用式(6)计算得到。

(6)

式中：t——气瓶直筒段平均壁厚,mm；

μ——气瓶材料泊松比；

E——气瓶材料弹性模量,MPa。

将式(6)代入式(5)，得到气瓶进液量与试验压力的关系式为：

×(1+pβt)+Vpβt

(7)

2 实例验证

2.1 试验描述

以某大容积高压钢质无缝气瓶为例，通过对其进行液压试验，验证理论计算公式的正确性。图1为试验气瓶的几何结构， 其主要技术参数如表1所示。以水为液压介质， 采用液压试验系统对气瓶进行液压试验， 试验过程中自动记录系统进水量和试验压力值。在气瓶直筒段中部外壁粘贴应变片， 设置2个应变测点， 沿外壁周向均匀分布。试验过程中， 每升压一定压力间隔， 短暂停机保压， 采集各测点应变值， 直至液压试验结束。本试验所用应变片为某机械研究院生产的B×120-3BA型两向电阻应变计，栅长×栅宽为3 mm×2 mm，灵敏系数为2.08±1%，应变值经UCAM-60B静态数据应变仪读取。

图1 气瓶几何结构示意

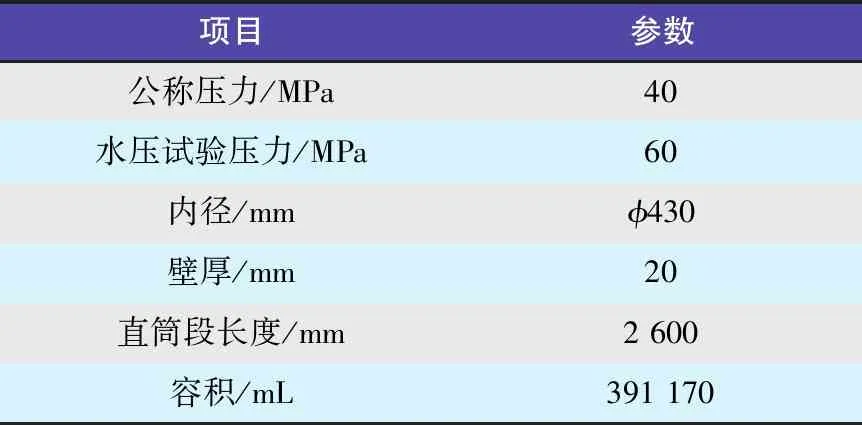
表1 气瓶主要技术参数

2.2 结果分析与讨论

实例以水为液压介质(此时进液量为进水量)，水的压缩系数βt按照式(8)计算【7】：

βt=(K×105-6.8p)×10-7

(8)

式中：K——与温度有关的系数，可通过查文献【7】附表得到。

以2个应变测点测得的轴向应变εz和环向应变εt平均值作为气瓶直筒段的轴向应变和环向应变值，将各参数代入式(5)，得到对应压力下进水量的理论计算值A，将试验压力和气瓶参数代入式(7)得到对应压力下进水量的理论计算值B。进水量的试验值和理论计算值与压力的关系曲线见图2。由图2可以看出，随着进水量的增加，压力线性增加，进水量的理论值A和理论值B均与试验测量值非常吻合，表明了理论计算公式的可靠性。表2分别列出了气瓶在试验压力达到公称压力40 MPa和水压试验压力60 MPa时，进水量试验测量值与理论计算值的误差。由表2可以看出，通过式(5)计算得到的理论值A与试验值的误差值为2.7%和3.3%，通过式(7)计算得到的理论值B与试验值的误差为2.0%和2.3%，误差很小。由图2和表2综合分析表明，尽管随着试验压力的增高，进水量的试验值与理论值A和B之间的差值逐渐增大，但在压力达到气瓶水压试验压力、理论计算值与试验值的误差达到最大时，仅为3.3%和2.3%，误差仍较小，这进一步验证了进水量理论计算公式的准确性。对比理论值A和理论值B与进水量试验值的误差，显然理论值B与试验实测值更为接近，表明经式(7)计算得到的进水量更精确可靠。究其原因，是因为理论值A是根据气瓶外表面的应变值计算得到的，而理论值B是依据气瓶中径处的应变计算值计算得到的，气瓶虽简化为薄壁结构，但实际仍存在一定厚度和径比，误差亦在所难免。就实际操作而言，由于理论值A需要实测气瓶瓶体直筒段外壁的应变，增加了时间和经济成本，而通过式(7)计算进液量更加直接，因此式(7)更适合作为气瓶液压试验进液量的理论计算式。

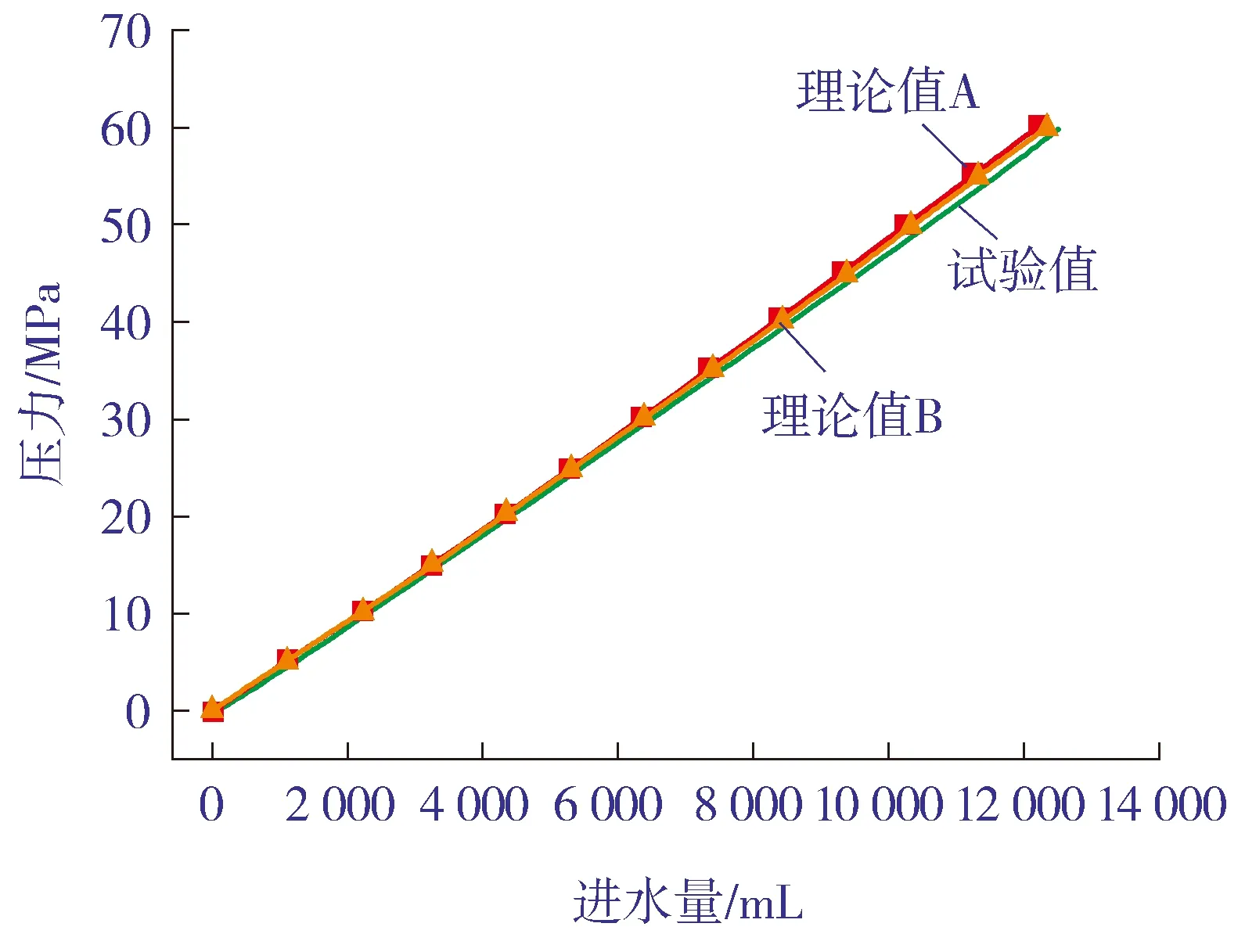
图2 压力-进水量曲线

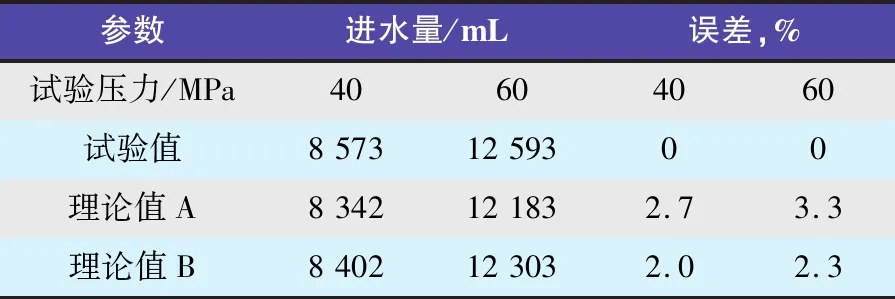
表2 进水量试验值与理论值的误差比较

依据前述理论分析，将式(7)给出的进液量分解为两部分，即气瓶的形变增量ΔV和试验介质——水的压缩量ΔVp。式(9)为分解计算式：

(9)

图3给出了气瓶总进水量及分解部分与压力的关系曲线。由图3可以看出，该气瓶水压试验进水量中，水的压缩量约占总进水量的80%，起主导作用，而气瓶内被压缩的水量中，气瓶初始内容积相比气瓶形变增量容积明显大很多，是导致总进水量较大的主要因素。因此，针对该气瓶，若试图减少气瓶在压力试验过程中的进水量，比如在耐压强度试验或液压疲劳试验时拟依靠减少进水量来降低试验周期、提高试验效率，则需要采取减小气瓶初始有效内容积的措施(如容积填充法【5】)，方可起到较为明显的效果。

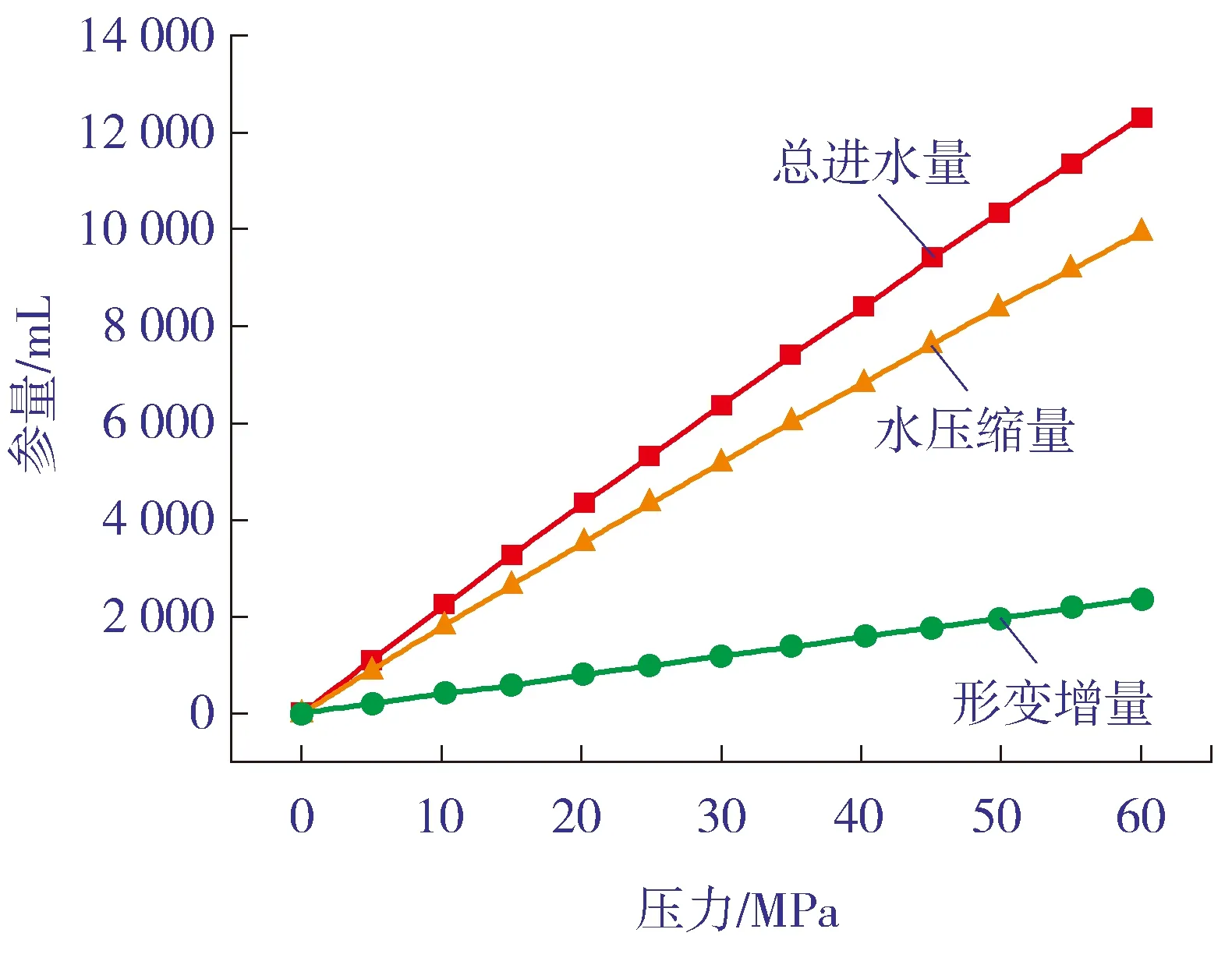
图3 气瓶各部分进水量与压力关系曲线

3 结论

1) 通过理论分析得到了气瓶液压试验进液量计算公式[式(7)]，可在已知气瓶基本参数情况下估算气瓶在一定压力下(限气瓶弹性变形范围内)的液压试验进水量，经实例试验，最大误差仅为2.3%，证明计算公式准确可靠，为获取气瓶液压试验进液量提供了快速有效的方法。

2) 将气瓶液压试验进液量分解为形变增量和试验介质压缩量，并给出了分解公式[式(9)]，为分析进液量的组成占比提供了理论依据。