孔隙介质水泥浆液渗透注浆有效扩散距离试验研究

张玉，郭豪，陈铁林，王荣鑫，程少振，廖晓东

(北京交通大学城市地下工程教育部重点实验室，北京，100044)

注浆技术广泛的应用于边坡工程、地基工程和隧道与地下工程等，在建筑结构补强、岩土文物保护、地质灾害治理、特殊地基改良、地下围岩加固、能源安全开采、固废高效处置、海洋环境修缮等领域有着特殊的作用，为建筑、交通、市政、管道、水利、矿业、能源、环境等工程建设运营安全提供重要保障，属于典型的治水补强兼顾型“非开挖原位加固技术”，拥有防治水和加固两大主要工程功能，具体涵盖防渗堵漏治突补强保久成型驱流减摩阻腐隔气灭火等[1-3]。注浆形式主要包括托底注浆、充填注浆、渗透注浆、压密注浆、劈裂注浆、切割注浆、喷射注浆和搅拌注浆等，对于孔隙介质常采用渗透注浆形式。在浆液满足可注性、流动性和功能性等的前提下，无机颗粒型浆材因成本低强度高污染少等特点而备受青睐，如黏土浆、石灰浆、水泥(细水泥)浆等[2]。然而，颗粒型浆材渗透注浆也面临3 个方面的问题[1-3]：1) 浆液的稳定性差、易产生离析；2) 渗透过程中存在渗滤效应，影响注浆效果；3) 浆液具有黏时变性，流动性随时间逐渐变差。其中，不稳定性和黏时变性问题可通过掺加助剂得以解决，如水泥浆中掺加膨润土可降低其离析率，掺加水玻璃可弱化其黏时变性。而渗滤效应则是难以避免的，只能从本质上对其进行研究，明确其对注浆效果的影响并得出正确的判定计算方法，进而为多孔岩土体或人工填筑层介质注浆工程的科学设计和施工提供依据。扩散距离是渗透注浆的一个重要参数，它和孔隙率、水灰比、注浆压力和注浆时间等影响因素有关，而对于存在渗滤效应的渗透注浆技术，结合工程实践和理论分析[1]，存在一个“有效加固范围”的问题，即涉及“有效扩散距离”的计算，因此，对孔隙介质水泥浆液渗透注浆有效扩散距离进行研究具有一定的工程意义和实践价值。当前，针对考虑“渗滤效应”有效扩散距离计算的研究较少，特别是注浆时间这个因素往往被忽略。HERZIG 等[4]研究得到一种多孔介质中悬浮颗粒沉积堵塞的渗滤系数计算微分方程；ERIKSSON等[5]对过滤和孔径变化影响下的浆液注浆扩散进行了数值预测；BOUCHELAGHEM 等[6]通过足尺试验对饱和孔隙介质中浆液运移—稀释—滤出机制进行了分析；SAADA等[7-8]试验给出水泥悬浊液在孔隙介质中的流动模型和基本的渗滤特性，建立了一维渗透注浆的解析解；MAGHOUS等[9]建立了考虑颗粒渗滤的工程现场注浆模型；CHUPIN等[10]通过试验和模拟得出渗滤效应对砂柱中水泥基浆液注浆有明显的影响；KIM 等[11]考虑浆液的黏时变性和过滤作用，得出渗滤系数与介质粒径、水泥粒径和浆液浓度有关；KIM等[12]建立了模拟细水泥浆液在砂柱中渗滤的颗粒网格模型；陈星欣等[13]通过土柱试验分析了悬浮颗粒粒径和渗流速度对其迁移和沉积的耦合影响；房凯等[14]引入线性滤过定律，给出一种球孔扩散水泥浆液扩散模型；李术才等[1,15]通过数值计算对渗滤作用下的浆液扩散规律进行分析，提出了有效加固范围的概念，建立了砂土介质水泥浆液渗透扩散距离与孔隙直径、浆液颗粒质量分数和注浆压力的函数关系；张玉等[3]对不同扩散形式下考虑浆液黏时变性的渗透注浆理论模型进行了推导等。综上可知，现有研究主要集中在渗滤效应机制、渗滤系数计算和渗滤扩散规律等方面，为后续研究奠定了基础。而对浆液有效扩散距离计算，特别是涉及的浆液稳定性控制、有效扩散距离界定、渗滤效应空间机制等应用研究较少，且渗滤效应对注浆效果的影响过程复杂，无法得到准确的理论模型进行计算和解释，故有必要对孔隙介质水泥浆液渗透注浆有效扩散距离进行试验研究。

1 试验方案

结合试验目的，拟针对浆液在孔隙介质材料中的“一维”或“单向”渗透问题进行研究，并尽可能多地记录和量测可获取的数据，如扩散距离、注浆时间、渗流量、水灰比等。该试验对试验设备的可行性、试验材料的稳定性、试验设计的合理性、试验系统的密封性等要求较高，现分别对其进行说明。

1.1 试验设备

在已有研究[1,15]的基础上，根据试验需要，自主研制“一维渗透有机玻璃分段拼接式注浆管系统”，该系统主要包括注浆设备和模型管道，具体由空压机、调压阀、储浆罐(有机玻璃制)、有机玻璃管、反力架、阀门、压力表、量筒、量杯、输浆管、输气管和秒表等，具有“全段全程可视化”的特点，如图1所示。其中，有机玻璃注浆管由6节相同的短管(内径为10 cm、长为30 cm)通过法兰板连接而成，总长为1.8 m，从下往上依次进行编号，并画出每节的中线。为保证法兰板连接处的密封性、避免注浆口和出浆口被颗粒材料堵塞、方便注浆和拆卸，在注浆管两端和中间标准段连接处分别制作了“硅胶密封隔离垫”。

1.2 试验材料

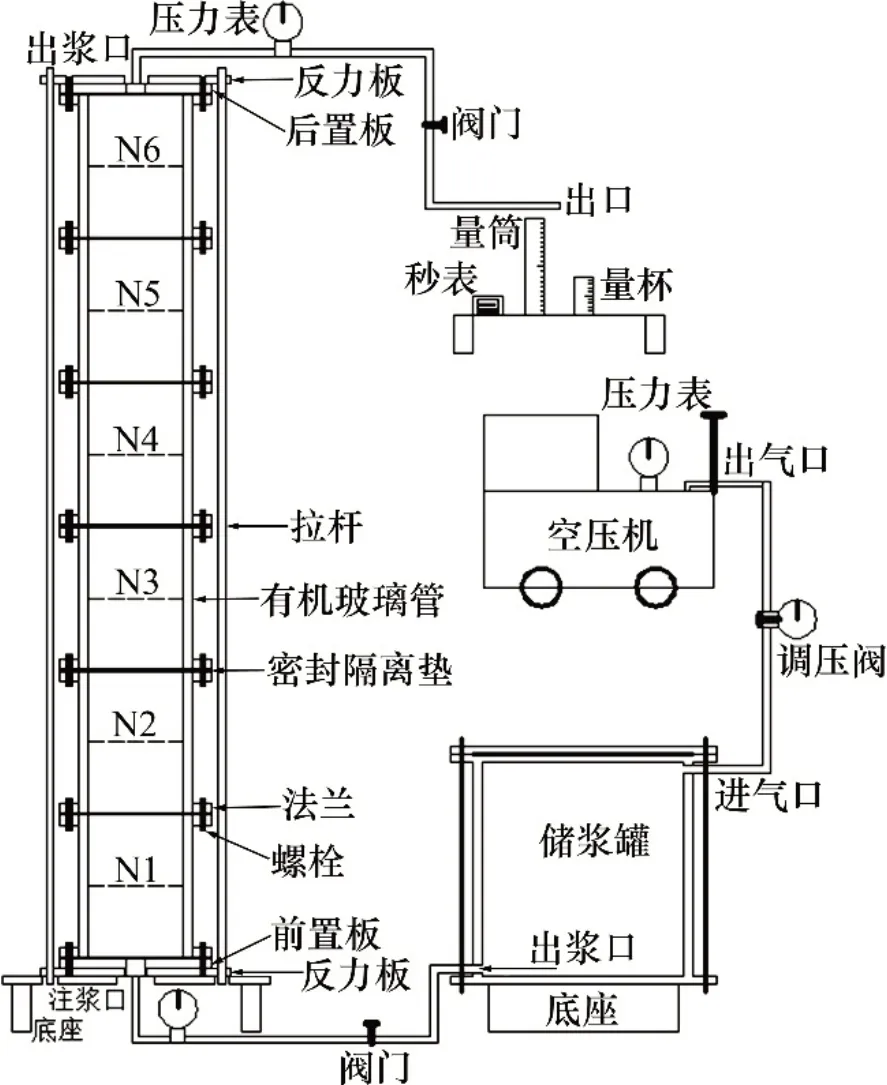
图1 一维渗透有机玻璃分段拼接式注浆管系统Fig.1 Subsection-splicing grouting system by plexiglass for one-dimensional permeation

试验中，孔隙介质材料采用碎砾石，最小直径为2.0 mm，最大粒径为15 mm，相对密度为2.73，颗粒级配如图2所示。碎砾石的颗粒累计质量分数小于10%，20%，30%，50%，60%和95%对应的粒径分别为d10，d20，d30，d50，d60和d95，经计 算，d10=4.812 8 mm，d20=5.874 9 mm，d30=6.694 7 mm，d50=7.998 6 mm，d60=8.551 5 mm，d95=10.192 5 mm，故不均匀系数为1.78，曲率系数为1.09。

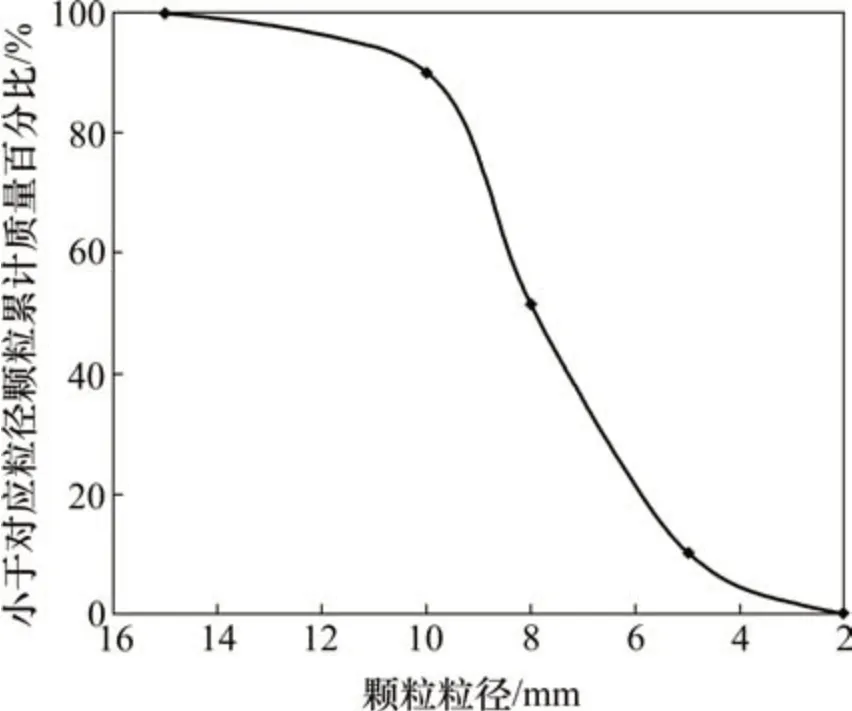
图2 碎砾石的颗粒级配曲线Fig.2 Granule gradation for crushed gravel

水泥选用河北燕新建材有限公司生产的P.O42.5R 普通硅酸盐水泥，相对密度为3.1，颗粒粒径为50～75 μm。膨润土使用钠质膨润土，蒙脱石质量分数为80.0%，莫氏硬度为2.0，密度为2.71 g/cm3，细度为45 μm，最大吸水量为其体积的12倍，体积膨胀倍数最大达20倍，颜色为淡紫红，在试验中用作悬浮剂。

1.3 试验设计

试验中，主要考虑浆液扩散距离受孔隙率、水灰比、注浆压力和注浆时间这4 个因素的影响。为了得到扩散距离和4个因素之间的函数关系，有必要进行正交试验。由于注浆时间无法人为设定，它取决于实际注浆时间，以难以注入或浆液注完为准，故正交试验中暂不考虑注浆时间，而在之后的分析中通过记录实际注浆时间再加以考虑。因此，该试验采用“三因素四水平”模式。

碎砾石的孔隙率取值要同时满足水泥浆液可注性和人工填装程度的要求。试验中，浆液可注性的判定计算式如下[2]：

式中：Ng为可注性参数，Ng≥3；bj为岩土体的孔隙开度，mm；d95为浆液中颗粒累计质量分数小于95%对应的粒径，mm。

岩土体孔隙开度的计算式为[1]

式中：n为岩土体的孔隙率；d10为岩土体颗粒的有效粒径，mm。

通过预装和计算，碎砾石的孔隙率依次取47.04%，43.87%，40.71%和37.23%，即每节有机玻璃注浆管的填装质量依次为3.35，3.55，3.75 和3.97 kg。

试验中，为了使浆液具有较好的流动性，要求水泥浆液流动方程满足牛顿流体，即τ=μγ(其中，τ为剪切力，Pa；μ为浆液的动力黏度，mPa·s；γ为剪切应变，s-1)。根据经验，水灰比(即水与水泥的质量比)大于2.00 的浆液无法保证注浆效果[15-16]，牛顿流体浆液的水灰比不小于1.00[17]，故水灰比依次取1.25，1.50，1.75和2.00。

注浆压力是根据现有设备量程和参考已有研究[1]进行取值，依次为50，100，150 和200 kPa，采用恒压注浆。根据三因素四水平正交试验表，可得出16组不同的试验组合，如表1所示。

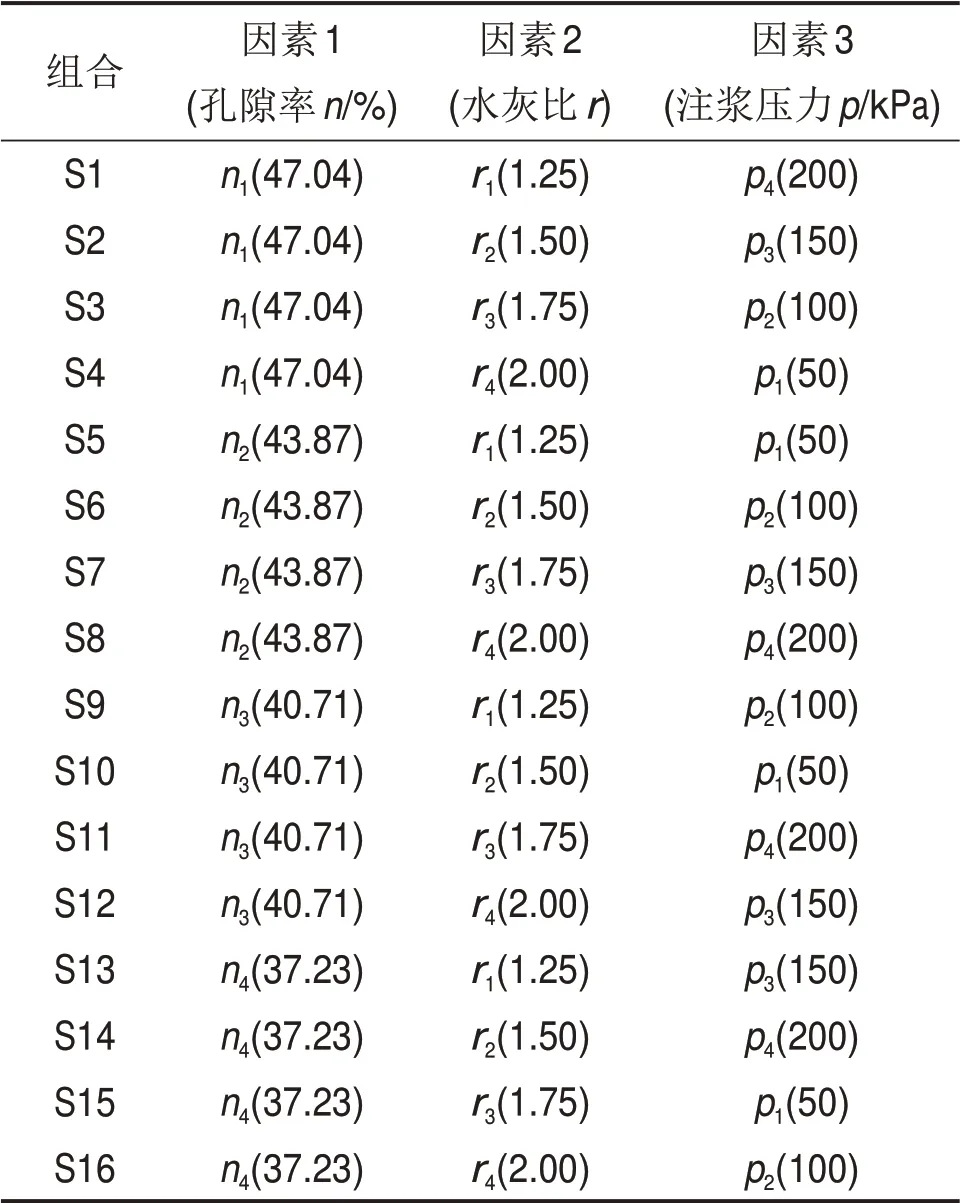
表1 正交试验组合Table 1 Orthogonal experiment combination

2 试验控制

试验按照“配料—填装—压水—注浆—拆卸”的顺序进行，针对水泥浆液的不稳定性、黏时变性、流动性、制浆量和诱导期以及试验系统的密封性等，均需要进行合理控制和计算，以便保证注浆实施效果。

2.1 水泥浆液的不稳定性和黏时变性

水泥浆液具有明显的离析效应，即稳定性差，不利于保证浆液的流动性，且凝结体易发生收缩，有必要对其进行改善。常用的方法有物理搅拌法和化学改性法。物理搅拌法是指注浆过程中使浆液处于动态搅拌状态，可防止其发生离析，该方法对注浆设备有特殊要求，影响系统稳定性，且不能改善水泥浆凝结体的收缩。因此，该试验选用化学改性法，即通过掺加某种助剂(悬浮剂)，使得浆液增稠、形成网架支撑或具备触变性能，以此降低浆液的离析率并改善其收缩性能。试验中使用的悬浮剂为无机钠质膨润土，以P.O42.5R 普通硅酸盐水泥为例，设定以30 min 离析率为5.0%作为控制值[1](30 min是根据水泥浆液初凝和注浆时间需要设定的)，通过多次试验，综合考虑浆液黏度，得到不同水灰比浆液的最佳膨润土质量分数，如图3所示。

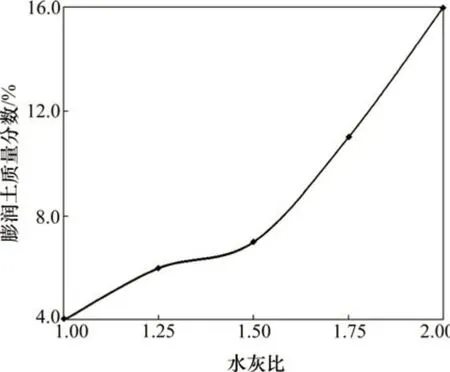
图3 不同水灰比浆液的最佳膨润土质量分数Fig.3 Optimum bentonite mass fraction under different water-cement ratios

由图3可以看出：实际测出的30 min离析率处于4.6%～5.6%之间，平均为5.1%，符合要求。水灰比越大则最佳膨润土质量分数越大。当水灰比大于1.50 时，变化速率突然增高，其原因是当水灰比大于1.50 时，浆液的离析率和离析速率均较大，且离析在30 min 内基本完成，导致膨润土质量分数增加较多。

通过对掺加膨润土水泥浆液的黏度测试，分别得到不同水灰比浆液的恩式黏度-时间关系曲线，如图4所示。

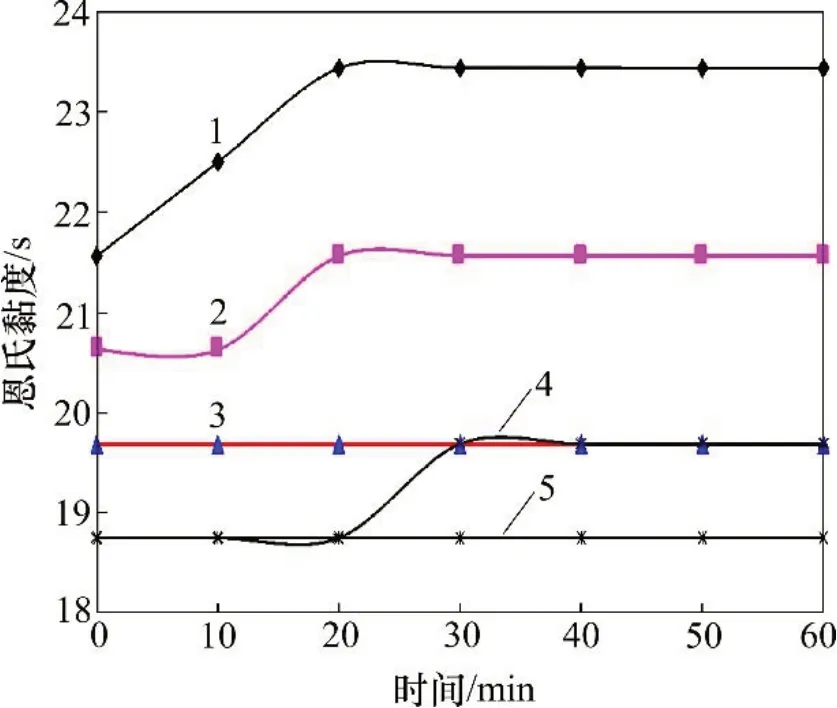
图4 不同水灰比浆液恩氏黏度-时间关系Fig.4 Engler viscosity-time curves under different water-cement ratios

由图4可以看出：掺加膨润土的水泥浆液恩氏黏度在60 min 内随时间基本不变，误差为1～2 s，说明掺加膨润土的水泥浆液不仅稳定性强，且黏时变性好。通过换算，可以得到不同水灰比(1.00，1.25，1.50，1.75 和2.00)浆液的动力黏度分别为2.51，2.19，1.97，1.86和1.76 mPa·s。

2.2 水泥浆液的流动性

试验中碎砾石粒径和孔隙率较大，根据可注性计算和恩氏黏度量测结果可以判定水泥浆液的流动性较好[1]。另外，在将搅拌好的浆液倒入储浆罐时，使用直径为0.25 mm的筛网进行过滤，去除浆液中可能存在的较大絮状物。

2.3 试验系统的密封性

对于有“流体”参与的试验，试验系统的密封性至关重要。试验中，为保证注浆过程中浆液“不渗不漏不突”，注浆前，运用同等的注浆压力先进行压水试验，检测系统的密封性，并用反力架保证系统的整体性和稳定性。若发现渗水问题，则对其进行再次紧固并反复压水直至不渗为止。以孔隙率为37.23%、注浆压力为200 kPa为例，在当前试验条件下，渗流时进水口和出水口压力分别为168 kPa 和118 kPa，饱和时分别为198 kPa 和196 kPa，5 s的渗流量为590 mL。

2.4 制浆量和诱导期

制浆量和诱导期是注浆工程中2 个重要的参数，直接影响施工成本和注浆效果。在实际工程中，制浆量主要取决于岩土体的孔隙率，诱导期主要取决于扩散时间。试验中，最大的浆液量为难以注入时消耗的浆液总体积，考虑到无法事先估算且试验中注浆时间也无需太长，故制浆量统一取储浆罐的体积14.14 L，其中浆液有效体积为11.31 L。因此，试验的停注时间取决于难以注入或浆液注完。

由于浆液在30 min 内的稳定性好、不存在黏时变性，故试验中设定最大注浆时间为30 min。拆卸时间以不影响试验量测且不损坏试验装置为准，试验表明注浆体在凝结5～6 h时已基本成型，若时间超过6 h，则会导致注浆体和有机玻璃内壁黏结，不便于拆卸。

3 试验结果

通过试验，得到不同试验组合浆液的扩散距离、扩散速度、渗流量和时间的关系，以及水灰比和扩散距离的关系。以S10 和S14 试验组合为例，试验过程如图5所示。基本假定为：1)忽略膨润土对浆液密度的影响；2)浆液密度按理论式进行计算；3) 忽略储浆罐浆液自身压力的影响；4)每节有机玻璃管注浆体均匀连续分布；5)忽略碎砾石在注浆过程中发生的极小压缩或移动；6)忽略扩散距离因碎砾石曲折度和接触面粗糙度引起的测量误差。

3.1 真实扩散距离

图5 渗透注浆试验过程Fig.5 Experimental processes of permeation grouting

真实扩散距离指试验中浆液实际能达到的最大扩散距离。通过试验，记录每个试验组合的分段扩散时间，然后得到扩散距离、扩散速度与时间的关系(以S6 和S14 试验组合为例)，如图6所示。最后，以扩散速度为0.1 cm/s(当扩散速度为0.1 cm/s时，试验中认为浆液已难以注入)、注浆时间为30 min 和浆液有效体积为限值，即可计算得到每组试验的真实扩散距离，如图7所示。其中，由于扩散速度为每15 cm距离的平均速度，故在扩散速度计算时扩散时间采用中值。

由图6可以看出：当孔隙率、水灰比和注浆压力一定时，浆液扩散距离随时间不断增加，基本呈对数函数关系，原因是注浆压力的耗散、浆液颗粒的淤积等导致扩散速度随时间不断减小。以S14试验组合为例，孔隙率、水灰比和注浆压力分别为37.23%，1.50 和200 kPa，经计算，真实扩散距离为371.53 cm，用时583.21 s。某些试验组合中，扩散速度并非一直减小，特别是在100 cm 扩散距离内存在一定的波动现象，原因可能是浆液驱使气体流动受到影响[1,15]。

3.2 浆液渗流量和密度

试验中，为了解浆液的渗透性，量测每组试验中浆液的流量，并称其质量。以浆液流出时为0时刻，量测5 s时的流量，间隔时间为30 s，总量测时间根据实际而定。以S6和S14试验组合为例，试验结果如图8所示。

由图8可以看出：随着时间的变化，浆液渗流量不断减小，说明碎砾石渗流系数在不断减小。浆液密度同样随时间不断减小，说明流出的浆液并非制备的初始浆液，而是在渗透过程中发生过滤作用后的浆液。以S14试验组合为例，流出浆液0 时刻的密度为1.36 g/cm3，小于浆液的初始值，而180 s时降低至1.29 g/cm3。因此，碎砾石的孔隙率由于过滤作用不断减小，进而导致渗流系数降低，过滤作用存在明显的时间效应。其中，S6 试验组合由于注浆时间短而只测量到2个数据。

图6 浆液扩散参数与时间的关系Fig.6 Curves of slurry diffusion parameters with time

3.3 有效扩散距离

图7 各试验组合的真实扩散距离Fig.7 Real diffusion distance for every experiment combination

图8 浆液渗流量和密度随时间的变化Fig.8 Curves of slurry seepage quantity anddensity with time

相对于真实扩散距离，符合设计要求的距离可称为“有效扩散距离”或“有效加固范围”，有效扩散距离的判定指标要依据工程的注浆目的而定。注浆技术的工程功能主要包括防治水和加固。作为渗透注浆，一方面能降低岩土体的渗透性，另一方面也能对其进行补强，因此，从防治水和加固2个角度，可列出有效扩散距离的3种判定式如下式所示：

式中：kg为注浆体的渗流系数，cm/s；[k]max为设计允许的注浆体最大渗流系数，cm/s；σc为注浆体的抗压强度，MPa；[σc]max为设计允许的注浆体最小抗压强度，MPa。

式(3)中的判定式分别适用于工程防治水、补强、防治水和补强3种工况要求。试验中，由于注浆后需及时拆卸，而此时注浆体并未完全凝结，未能实现渗流系数和抗压强度的准确测量，考虑到渗流系数与孔隙率有关[18]、抗压强度和水灰比有关[15]，拟选用等价的判定式进行置换，如下式所示：

式中：nr为注浆体的剩余孔隙率；r为浆液的水灰比。

由于水泥浆液中掺加了钠质膨润土，稳定性好且具有一定的膨胀性，所以，当1.00≤r≤2.00 时注浆体的剩余孔隙率可忽略不计。因此，可通过注浆体中浆液的实际水灰比来综合判定浆液的有效扩散距离。

3.3.1 有效扩散距离的计算

注浆体中浆液的实际水灰比可通过注浆体质量增加量、 初始孔隙率和密度计算式反算得到，如式(5)所示。注浆后6 h即可进行拆卸，然后称量每节注浆体的“质量增加量”，计算其浆液密度，然后反算浆液的实际水灰比。

式中：ρs为浆液的密度，g/cm3；mi为注浆体的“质量增加量”，kg；Vv为注浆体的初始孔隙体积，cm3；ρc为水泥颗粒的密度，取3.1 g/cm3；ρw为水的密度，取1.0 g/cm3。

式(5)中的水灰比计算式为理论公式，经试验计算，水泥浆液的理论密度和实测密度基本相等，后者略微偏小，这是由于实际浆液中含有少量气泡。通过计算，可得到水灰比-扩散距离关系曲线，以S6和S14试验组合为例，水灰比-扩散距离关系曲线和凝结体实物状态分别如图9和图10所示。以水灰比2.00 为临界值，以真实扩散距离为限值(若有效扩散距离计算值大于真实扩散距离，则按真实扩散距离取值，即le≤lr(le为浆液的有效扩散距离，cm；lr为浆液的真实扩散距离，cm)，计算得到不同试验组合的有效扩散距离，如图11所示。由于浆液水灰比为每节注浆体30 cm距离的平均值，故在计算时采用扩散距离中值。

由图9可以看出：随着扩散距离的增大，浆液的水灰比不断增加，基本呈线性增加趋势，同样说明了渗滤效应的作用及其明显的空间效应，同时也验证了“有效扩散距离”的存在。值得注意的是，在大部分试验组合中，注浆口附近一定距离内的注浆体水灰比小于浆液的初始水灰比，以S6 试验组合为例，在扩散距离100 cm 内，注浆体中浆液的水灰比小于1.50，这是由于注浆口附近一定距离内的渗滤效应更为明显。三峡工程水泥浆液注浆施工中，经常遇到吸水不吸浆、失水回浓和吸水多吸浆少的工程现象[16]，可能与水泥浆液渗透的“渗滤效应”有很大关系，因此，有必要对渗滤效应机制进行深入研究，明确渗滤效应作用下渗流系数的变化规律，以便更好地进行浆液水灰比“动态设计”和“材料复合型”分步注浆，同时建议浆液的设计水灰比适当提高0.1～0.2，不仅便于注浆，同时节省材料。另外，根据不同扩散距离的浆液水灰比差值和变化规律可以看出，浆液水灰比的变化不存在突变，故取每节注浆体30 cm长是合理的，不存在显著的跨度效应。

图9 水灰比与扩散距离的关系Fig.9 Curve of water-cement ratio with diffusion distance

图10 凝结体实物状态Fig.10 Actual statuses of grouting body

由图10可以看出：从注浆体成型或凝结的角度，在同等条件下，首节到末节依次由致密变为松散，密实性和黏结性越来越差。从注浆体颜色的角度，在同等条件下，首节到末节依次由深灰色逐渐变为黄灰色。说明孔隙介质水泥浆液渗透注浆过程中渗滤效应的存在和对注浆效果的影响。因此，由于浆液渗透过程中的过滤作用，使得浆液沿渗透方向分布不均匀，主要体现在浆液水灰比的变化，距离注浆口越远水灰比变得越大，注浆效果达不到工程设计要求。其中，S6 试验组合中注浆体上的裂缝是人工拆卸所致，S14试验组合中注浆体尚未基本成型的原因是拆卸时间相对过早。

结合浆液渗流量和密度、注浆体中浆液水灰比的变化规律，可以看出，渗滤效应具有明显的时空效应，不仅与渗流时间有关，也与扩散距离有关。在垂直于渗透方向上，渗流系数随时间不断减小；在平行于渗透方向上，水灰比随扩散距离逐渐增大。

3.3.2 真实和有效扩散距离的对比

为了直观地了解有效扩散距离和真实扩散距离，明确它们之间的区别和关系，现将各试验组合的扩散距离结果进行对比，如图12所示。

由图12可以看出：有效扩散距离与真实扩散距离之比为0.52～1.00。因此，水泥浆液渗透注浆工程中要考虑渗滤效应的影响，特别是注浆孔间排距的设计要参照有效扩散距离。

图11 各试验组合的有效扩散距离Fig.11 Effective diffusion distance for every experiment combination

图12 扩散距离的对比Fig.12 Comparison of diffusion distance

3.3.3 有效扩散距离的计算式

有效扩散距离主要受孔隙率、水灰比、注浆压力和注浆时间等因素的影响，为了实现定量计算，现根据试验结果建立有效扩散距离和4个影响因素的函数关系：

式中：le为浆液的有效扩散距离，cm；pg为注浆压力，kPa；t为注浆时间，s。

基于渗透注浆经典马格理论，一维、二维和三维渗透下的注浆半径计算式[3]分别如式(7)～(9)所示。

式中：H为注浆压力水头，cm；h0为孔隙压力水头，cm；r1为注浆半径，cm；k为浆液的渗流系数，cm/s；r0为注浆管或浆泡的半径，r0≪r1，cm；K为土体的渗流系数，cm/s；η为浆液与水的运动黏滞系数的比值。

由式(7)～(9)可以看出：注浆半径与孔隙率、浆液运动黏度、注浆压力和注浆时间均呈幂函数关系，而浆液运动黏度和水灰比也呈幂函数关系[3]，故设定有效扩散距离计算式符合幂函数数学模型，如下式所示：

式中：a为常系数；x1，x2，x3和x4为指数常数。

通过对数变换可得到其对数形式：lnle=x1lnn+x2lnr+x3lnpg+x4lnt+ lna，将试验结果代入式(10)求最优解可得到有效扩散距离的对数形式计算式，如下式所示：

现将式(11)的对数形式计算结果和试验结果进行对比，如图13所示。

图13 le对数形式计算结果和试验结果的对比Fig.13 Comparison between logarithmic calculating and experimental results ofle

由图13可以看出：有效扩散距离的自然对数计算结果和试验结果比较接近，波动范围为±5.0%，平均偏大0.08%，说明计算结果较为可靠。因此，有效扩散距离的计算公式如下：

将式(12)的有效扩散距离计算结果和试验结果进行对比，如图14所示。

由图14可以看出：有效扩散距离的计算结果和试验结果整体上比较吻合，平均偏大2.1%，但在部分试验组合中相差较大，波动范围为-24.28%～28.59%。为偏于保守设计，使计算结果整体上更接近或小于试验结果，建议对式(12)赋予1 个折减系数。通过试算，以10.0%为波动上限，折减系数的取值范围为0.77～0.86，以0.86 和0.77为例，有效扩散距离的计算式如式(13)所示，计算结果和试验结果的对比如图15所示。

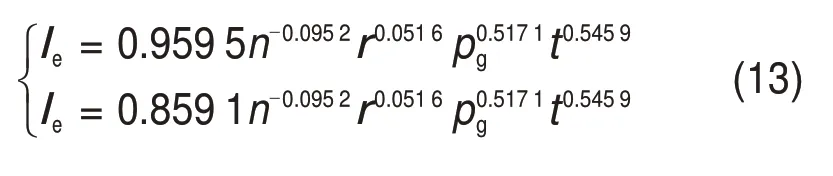
根据试验结果和有效扩散距离计算式，通过极差和极值综合分析[19-21]得到了有效扩散距离的影响因素敏感性，显著程度从大到小依次为孔隙率、水灰比、注浆压力和注浆时间。

3.3.4 不同计算模型的对比

一维渗透注浆浆液扩散距离的计算模型主要有基于达西定律的不考虑和考虑渗滤效应的2个模型[3]，计算式分别如式(7)和式(14)所示。

式中：k(t)为浆液的实时渗流系数，cm/s；K(t)为岩土体的实时渗流系数，cm/s。

在式(7)和式(14)中，渗流系数K可通过室内常规实验或固结反演法进行量测。为了计算方便，也可采用既有成熟的经验计算方法，如土体渗流系数等效计算方法太沙基模型[18]，如下式所示：

式中：e为岩土体的孔隙比；λ为无效孔隙比与有效孔隙比(或无效孔隙体积与有效孔隙体积)的比值。土体一定时，该值为常数。对于粗粒土，λ=0。

由于渗滤效应的影响，土体的渗流系数随时间变化，主要体现在孔隙率的变化，如下式所示[1,4,11]：

图14 有效扩散距离计算结果与试验结果的对比Fig.14 Comparison between calculating and experimental results

图15 有效扩散距离折减计算结果与试验结果的对比Fig.15 Comparison between reduced calculation and experimental results

式中：σ为t时间内渗滤的水泥浆液颗粒体积，cm3；β为水泥颗粒的膨胀系数，一般取2.0～3.0；α为水泥浆液的渗滤系数，其值与滤过速率和滤过系数有关，s-1；ω为水泥浆液中水泥颗粒的质量分数；V为岩土体的总体积，cm3；n(t)为岩土体的实时孔隙率。

将式(16)代入式(15)，令λ=0，即可得到粗粒土渗滤效应作用下的渗流系数计算式，如下式所示：

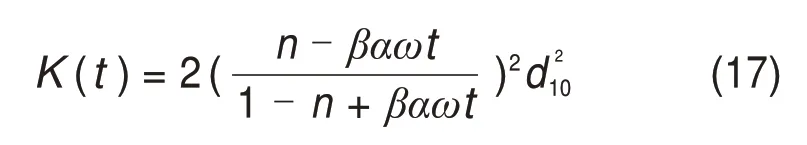
分别联合式(15)和式(7)、式(17)和式(14)，即可求得不考虑和考虑渗滤效应的浆液扩散距离理论结果。将2种模型的理论结果与有效和真实扩散距离试验结果进行对比，如图16所示。其中，在考虑渗滤效应时，β取1.0，即认为水泥浆液渗流过程中不发生膨胀效应。根据文献[4]，当浆液颗粒粒径为4～125 μm、多孔介质粒径为700～2 000 μm时，渗滤系数为1.6×10-2～4.0×10-2s-1，故按照线性插值取渗滤系数α为15.1×10-2s-1。

由图16(a)可以看出：不考虑渗滤效应的理论计算结果小于真实扩散距离，但整体上又大于有效扩散距离，平均偏大6.1%，波动范围为-32.32%～46.58%。由图16(b)可以看出：考虑渗滤效应的理论计算结果小于真实扩散距离(除S11，S13和S14这3个异常点外)，且小于不考虑渗滤效应的理论计算结果，但整体上大于有效扩散距离，平均偏大5.1%，波动范围为-32.55%～28.39%。考虑渗滤效应的理论计算模型存在误差和异常点的原因在于受渗流系数计算方法和渗滤系数取值等的影响。因此，相对于真实扩散距离，理论模型计算结果均偏小，而对于有效扩散距离，理论模型计算结果均偏大，故基于试验的有效扩散距离计算结果相对比较合理，可为注浆工程设计提供参考。

图16 扩散距离理论计算与试验结果的对比Fig.16 Comparison between theoretical and experimental results of diffusion distance

4 渗滤效应影响机制分析

由试验结果可以看出，渗滤效应是指浆液渗透过程中，由于孔隙介质的过滤作用，使得浆液颗粒偏离其运动轨迹，不断停滞、沉淀、吸附、淤积，进而占用空间减小孔隙开度，改变孔隙介质的渗透性，直至最后堵塞渗透通道，引起浆液水灰比的变化，具有明显的时空效应。

根据浆液渗流量和密度、注浆体中浆液水灰比随时间的变化规律，现通过直观的形式对渗滤效应机制进行探讨。首先，将渗滤过程分为2个部分：1)渗滤进行。由于浆液颗粒渗滤的形成需要一定的时间，在此之前，认为浆液主要发生渗透，而渗滤效应尚未完成；2)渗滤完成。浆液渗透一定时间后，浆液颗粒完成了渗滤，此时过滤作用开始启动。因此，完整的渗滤过程是浆液渗透和渗滤完成的循环过程。根据试验结果，渗滤进行和完成的长度可取为30 cm，即单节有机玻璃注浆管的长度。现以4节有机玻璃注浆管为例，分析浆液渗滤效应的形成过程，如图17所示，图17中黑粗线条代表渗滤沉淀的浆液颗粒，但位置和粗细并不代表其真实状态和数量比例。

由图17可以看出：浆液颗粒的渗滤是逐步完成的，前一节渗滤后的浆液流入下一节继续渗滤，依次循环。横向上，浆液颗粒沉淀数量随时间不断增加；纵向上，浆液颗粒沉淀数量随扩散距离发生变化，且依次相对减少。浆液颗粒沉淀数量的增大直接导致孔隙率和渗流系数的减小，故渗滤效应影响下的“变渗流系数”是时间和扩散距离的函数，和试验结果分析相一致。

图17 渗滤效应形成过程Fig.17 Forming processes of percolation effect

孔隙体积一定的情况下，浆液颗粒沉淀数量的变化代表水灰比的变化，而水灰比也是有效扩散距离计算的重要判定指标。因此，浆液水灰比的变化是渗滤效应的重要体现。现以水灰比为研究对象，分析其变化过程和特点。由于浆液渗透是循序渐进的过程，为了表达方便，现使用矩阵形式进行描述，建立浆液渗透过程的“水灰比变化矩阵”，如下式所示:

式中：i和j分别为浆液渗透到的注浆管节数和注浆管自身所在节数；i≥1；j≥1。

由式(18)可以看出：r11即为浆液的初始水灰比，且ri1≤r11，rij≤ri(j+1)≤ri(j+2)≤…≤ri(j+m)≤…，m≥1。因此，浆液经过渗滤作用后，水灰比沿渗透方向不断增加，距离注浆口较近处的水灰比小于初始水灰比，造成“近端水灰比小渗流系数小、远端水灰比大渗流系数大”的矛盾现象，与试验结果相一致。因此，渗滤效应不仅影响注浆效果，也会导致后期注浆困难，不利于注浆工程的顺利实施。

5 渗滤效应理论模型探讨

试验研究和机制分析结果共同表明，渗滤效应作用下的浆液“变渗流系数”不仅随注浆时间变化，而且随扩散距离发生变化，而式(16)中只考虑了变量t，尚未考虑扩散距离的影响，这也可能是导致理论模型计算结果偏大的原因之一。因此，对于孔隙介质渗透注浆来说，有必要考虑渗流系数和注浆时间、扩散距离的关系。现基于达西定律，根据渗流量和孔隙体积的等量关系，建立一个可能存在的一维渗透理论计算模型：

由式(19)可以看出：若已知函数f(t)和f(r1)的表达式，则可进行求解，而这2个表达式只能通过大量室内试验分析得到。结合式(15)和式(16)，获取k(r1,t)等价于获取K(r1,t)和n(r1,t)，即

另外，注浆口近端水灰比小，渗流系数小，它对浆液渗透起着关键性作用，特别是决定着难以注入时间，现联合式(1)，(2)和(16)，可以得到考虑渗滤效应的浆液可注性判定计算式，如下式所示:

由于分析的是注浆口近端的影响，故不考虑扩散距离的影响。通过式(21)即可计算得到浆液的难以注入时间。

6 结论

1)当孔隙率、水灰比和注浆压力一定时，浆液扩散距离随时间不断增加，基本呈对数函数关系。随着时间的变化，浆液渗流量和密度不断减小，过滤作用存在明显的时间效应。

2)有效扩散距离的判定指标分别是渗流系数和抗压强度。随着扩散距离的增大，浆液的水灰比不断增加，基本呈线性趋势，过滤作用存在明显的空间效应。建议进行浆液水灰比“动态设计”和“材料复合型”分步注浆，设计水灰比可适当提高0.1～0.2，不仅便于注浆，同时节省材料。

3)渗滤效应具有明显的时空效应，不仅与渗流时间有关，也与扩散距离有关。在垂直于渗透方向上，渗流系数随时间不断减小；在平行于渗透方向上，水灰比随扩散距离逐渐增大。距离注浆口较近处的水灰比小于初始水灰比，造成近端水灰比小渗流系数小、远端水灰比大渗流系数大的矛盾现象。注浆口一定距离内的渗滤效应更为明显，对浆液渗透起着关键性作用，特别是决定着难以注入时间。因此，渗滤效应不仅影响注浆效果，也会导致后期注浆困难，不利于注浆工程的顺利实施。水泥浆液渗透注浆工程中要考虑渗滤效应的影响，特别是注浆孔间排距的设计要参照有效扩散距离。

4)有效扩散距离与孔隙率、水灰比、注浆压力和注浆时间这4个影响因素的函数关系符合幂函数数学模型。为了使得计算结果整体上更接近或小于实际值，建议赋予1个0.77～0.86的折减系数。影响因素敏感性显著程度从大到小依次为孔隙率、水灰比、注浆压力和注浆时间。相对真实扩散距离和有效扩散距离，理论模型计算结果分别偏小和偏大，基于试验的有效扩散距离计算结果比较合理，可为注浆工程设计提供参考。

5)考虑注浆时间和扩散距离这2个变量的渗流系数计算模型可能更适用于渗滤效应的理论计算。