循环荷载下无砟轨道-桥梁结构体系刚度退化性能

李龙祥，周凌宇，黄戡,2，张燕,4，赵磊

(1.中南大学土木工程学院，湖南长沙，410075；2.长沙理工大学土木工程学院，湖南长沙，410114；3.广西交通设计集团有限公司，广西南宁，530029；4.中铁上海设计院集团有限公司，上海，200070)

高速铁路无砟轨道-桥梁结构体系是一种竖向多层的空间结构，无砟轨道结构的服役期一般要求达到60 a，在高速列车荷载长期的高频振动和冲击以及温度循环作用下，加之各层结构材料性能的非一致性和边界约束的复杂性，将引起多层结构变形不协调，结构产生初始伤损，作为主要承重结构的钢筋混凝土材料损伤会不断累积。这些累积损伤将导致无砟轨道-桥梁结构体系协同工作性能退化，整个结构体系刚度降低，从而影响其平顺性和稳定性，从长远角度来看，会严重影响轨道结构的耐久性。结构体系在服役期内不会出现疲劳破坏[1]，为了保证无砟轨道-桥梁结构长期服役的稳定性及耐久性，研究列车荷载作用下无砟轨道-桥梁的疲劳损伤引起的刚度退化问题以及刚度退化后结构体系的受力性能变化问题具有非常重要的现实意义。对于混凝土材料以及无砟轨道结构的研究，国内外研究者采用有限元软件与疲劳累积损伤理论相结合的方法分析了双块式无砟轨道道床板在高速列车通过时的疲劳寿命[2-5]，并在对CA 砂浆疲劳与耐久性能试验研究的基础上，根据不同应力比下的疲劳寿命，得出CA砂浆在不同温度下的疲劳回归方程[6-8]。上述研究均是将轨道板及CA砂浆单独作为研究对象来分析其疲劳特性，没有考虑轨道系统作为一个整体结构时，各结构层协调工作下的结构疲劳损伤问题，同时，也未考虑列车荷载的周期性及随机性对轨道结构疲劳损伤的影响。为此，本文作者以CRTSⅡ型板式无砟轨道-简支梁桥结构体系为研究对象，建立3跨32 m双线简支箱梁+两端长30 m路基段的空间有限元模型，基于已有的材料疲劳损伤累积研究成果，对高速铁路桥梁在实际运营过程中疲劳累积损伤引起的结构体系刚度退化、荷载再作用时结构性能的变化规律进行研究。

1 有限元模型的建立

采用有限单元法，建立如图1所示的包括钢轨-扣件系统-轨道板-CA 砂浆层-混凝土底座-桥梁等主要结构的CRTSⅡ型板式轨道梁-体模型。钢轨视为弹性点支承梁，采用CHN60 轨，弹性模量取2.1×1011Pa，泊松比取0.3，容重取7 850 kg/m3，用空间梁单元模拟。其他构件的具体力学参数见表1。

扣件系统采用非线性弹簧单元模拟，根据“铁路无缝线路设计规范”[9]中关于WJ-8型扣件纵向阻力的限值规定反推出各方向刚度。目前关于混凝土与CA砂浆层界面性能的试验研究较少，本文根据刘学毅等[10-11]以及德国博格公司进行的推板试验，计算用于模拟界面间黏结性能的非线性弹簧的纵横向刚度。“两布一膜”滑动层摩擦因数取为0.2，同样用非线性弹簧模拟。

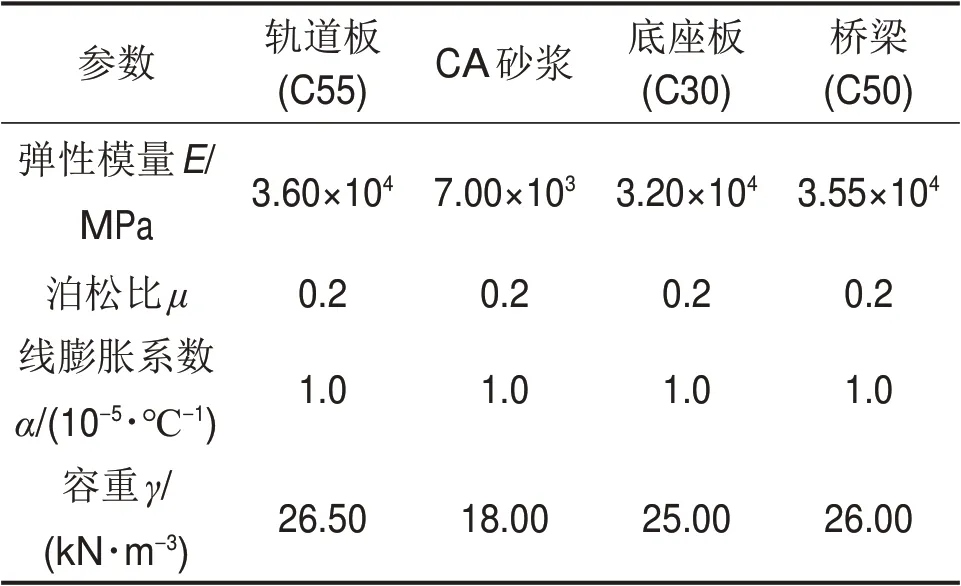
表1 CRTS II型轨道结构计算参数Table 1 Calculation parameters of CRTS II track structure

图1 有限元模型示意图Fig.1 Diagram of finite element model

2 结构刚度退化分析方法的确定

2.1 荷载模式与循环作用次数的确定

2.1.1 荷载工况分析

对于自然环境中的无砟轨道结构体系而言，除了列车循环荷载外，温度影响十分显著[12-14]，因此，对结构体系施加温度荷载或列车荷载或同时施加温度荷载和列车荷载。温度荷载包括竖向非线性温度梯度与整体降温，列车荷载仅考虑竖向静荷载，按规范[15]选取。本文所采用的竖向非线性温度梯度为戴公连等[16]研究得到的我国中部地区桥上CRTSⅡ型轨道结构温度梯度荷载模式，即

式中：θ1为距轨道板顶面不同距离处的温度；y为距轨道板顶面的距离。

结合式(1)对结构体系中轨道板顶施加正温度19.45 ℃，轨道板底施加正温度10 ℃。考虑到CA砂浆厚度较小，因此，CA砂浆整个厚度上均施加温度10 ℃；底座板顶与CA 砂浆黏结，所以，同样施加10 ℃；底座板底与简支梁桥面施加正温度5 ℃；桥梁顶板下表面施加2 ℃，桥梁顶板以下范围保持初始状态的0 ℃。结构体系在整体降温情况下，钢轨温度为-50 ℃，轨道系统温度为-30 ℃，桥梁温度为-20 ℃，暂不考虑桥梁与底座板材料因收缩而等效的降温幅度。

根据TB 10621—2014“高速铁路设计规范”，列车竖向活载按ZK 标准活载加载，且仅单线加载。

考虑温度作用和列车循环荷载3类作用因素的影响，本文主要计算以下4 种工况：工况1，正温度梯度；工况2，整体降温；工况3，单线列车荷载；工况4，整体降温+单线列车荷载。

2.1.2 循环作用次数的确定

对列车循环作用次数计算时，假设运营中该桥每10 min通过1个班次，则1 d(按20 h计算)内可以通过120班次。由于高速铁路无砟轨道的设计使用年限为60 a，故本文将每间隔10 a作为1个服役期节点计算结构体系在一定次数循环荷载作用后的受力性能，在设计年限内，不同服役期累积的循环荷载作用次数见表2。

由于每天中不同时刻的气温不同，因此，作用于桥梁上的温度梯度也因时而变。为了偏于安全计算，将任意时刻作用于结构体系上的温度梯度均按最大值加载，所以，本文计算中，将温度加载的频率等于列车荷载作用频率。循环荷载作用次数同样按照表2加载。

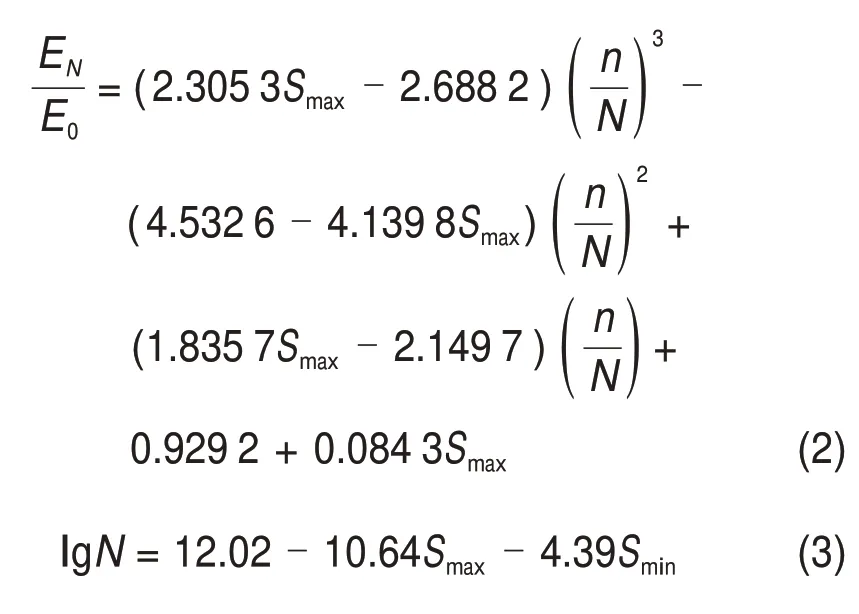
式中：Smax和Smin分别为最大和最小疲劳加载应力；n为循环荷载作用的次数；N混凝土的疲劳寿命；EN为混凝土加载N次后剩余割线弹性模量；E0为混凝土初始弹性模量。

表2 设计时间内不同服役期累积的循环荷载作用次数Table 2 Number of cyclic loads accumulated during different service periods during design time

2.2 循环荷载作用后材料剩余刚度的计算

国内外研究者在大量试验研究基础上给出了众多受压混凝土的疲劳方程，这些疲劳方程与试验环境、材料性能、混凝土配合比等条件密切相关。而构件刚度的退化程度主要由混凝土的剩余弹性模量表征，混凝土弹性模量随疲劳次数增加的衰减规律与其强度退化规律类似，宋玉普[17]通过对试验中混凝土加载N次后剩余割线弹性模量及泊松比随加载次数增加的变化规律进行总结，将混凝土割线弹性模量3个阶段的变化规律用回归公式表示，见式(2)与式(3)。

由式(2)与式(3)可计算出混凝土材料在整个疲劳寿命内弹性模量的退化规律。混凝土在循环荷载作用下其刚度退化在整个寿命阶段分为3 个阶段：第1阶段占疲劳寿命的10%左右，第2阶段占75%左右，第3阶段占15%左右。循环荷载作用次数N按照表2取值，取荷载共同作用(正梯度温度作用+列车竖向静活载)1次静力加载时结构各部位的应力。但考虑到结构各区域的应力并不一致，为了简化计算，将每跨简支梁分为3 段，见图2。由于结构的对称性，故将其编号为①号段和②号段，每段内的最大应力与最小应力均取该段内的应力平均值进行计算。由每段内的平均应力计算各段材料的疲劳寿命。基于以上分析可以得出混凝土剩余弹性模量与循环荷载作用次数的关系，见图3与表3。

图2 结构体系分段示意图Fig.2 Division of structure system

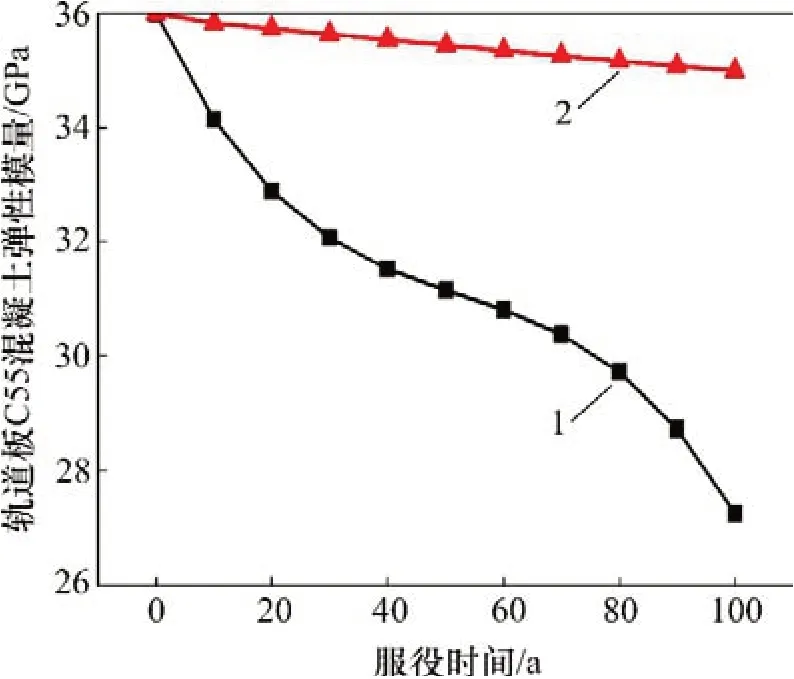
图3 C55混凝土剩余弹性模量与服役时间关系曲线Fig.3 Relationship between residual elastic modulus and service time of C5 5 concrete

基于上述分析可计算出简支箱梁在列车竖向静荷载与正温度梯度作用下的疲劳寿命N为7.8×109次。此寿命N的数量级非常大，可认为桥梁在100 a 的服役期内，在此荷载作用下并不会发生疲劳破坏，因此，本文在计算分析时不考虑32 m 简支梁的C50混凝土材料弹性模量随时间的变化。同时，假设CA砂浆材料的剩余弹性模量下降规律与混凝土的变化规律一致。不同服役期内轨道结构混凝土与CA 砂浆的剩余弹性模量计算值见表3。由表3可看出：1)结构支座附近受力较大，材料剩余弹性模量比跨中部位的小；2)结构跨中部位受力较小，材料寿命较大，因此，弹性模量变化较小。

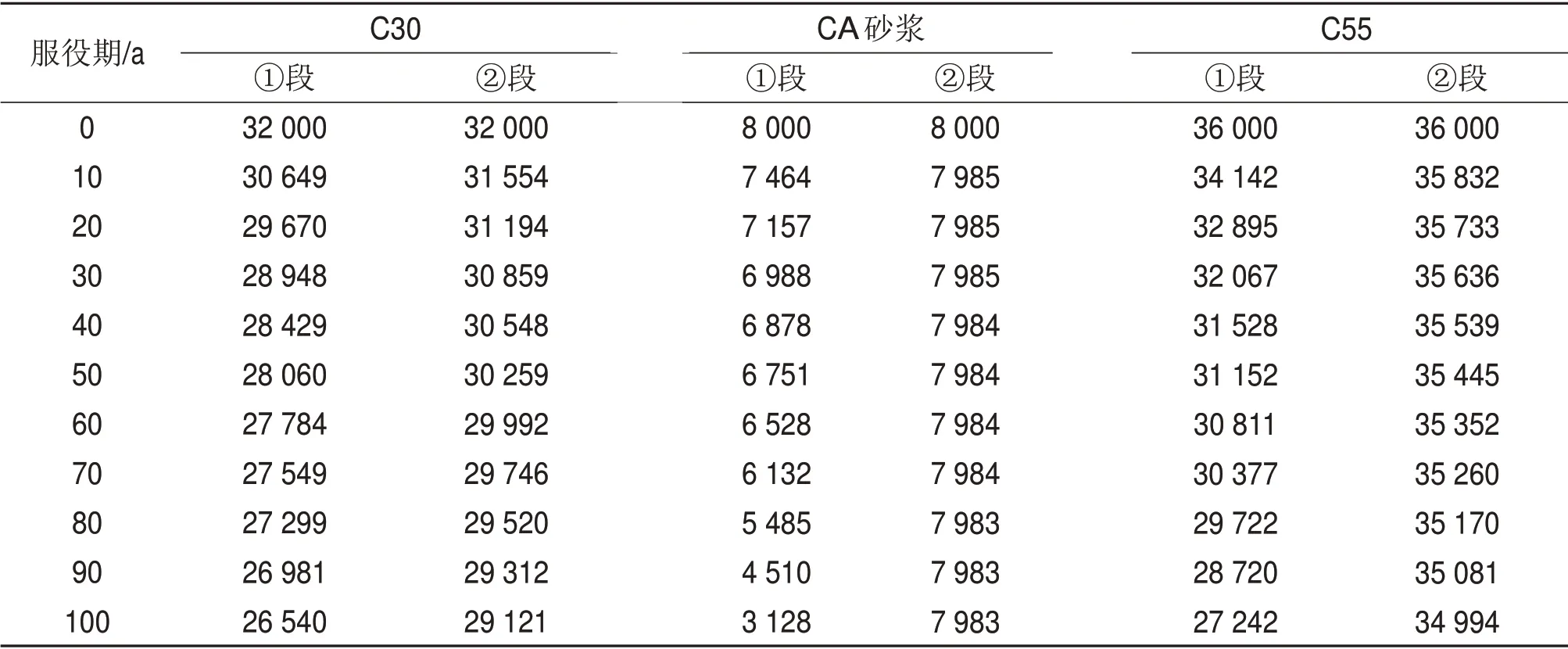
表3 材料剩余弹性模量计算结果Table 3 Calculation results of residual elastic modulus of material MPa

2.3 研究思路

首先，计算1 次静力(结构自重、预应力、正梯度温度与单线列车荷载共同作用)加载时整个结构体系各部位的应力水平；然后，确定出材料刚度退化曲线并根据不同服役期时的荷载作用次数构造出N次循环加载后的等效静力计算模型；最后，分别计算不同服役期时不同荷载工况下无砟轨道-简支桥梁结构体系的受力性能，从而得到结构体系在整个服役期内的经时性能演变规律。计算分析流程见图4。

图4 本文研究思路及分析流程Fig.4 Research idea and analysis processes

3 刚度退化后结构体系受力性能分析

3.1 正梯度温度作用下的结构受力分析

3.1.1 结构各层应力分析

图5所示为轨道板纵向压应力随结构服役时间的变化曲线。可见，轨道板在服役初始时纵向最大压应力为5.58 MPa，整体上，随着结构服役时间的增加，压应力逐渐减小，到结构服役100 a 时轨道板压应力减小到4.51 MPa；梁端处与跨中处应力稍有不同，但整体变化趋势相同。压应力变化可分为3 个阶段：第1 阶段为结构服役0～20 a，钢轨拉应力下降较快，占设计服役使用年限的20%；第2 阶段为结构服役20～80 a，占设计服役使用年限的60%，此阶段应力变化缓慢；最后阶段为结构服役80～100 a，应力再次快速下降。与材料疲劳作用下剩余刚度曲线变化规律保持一致。

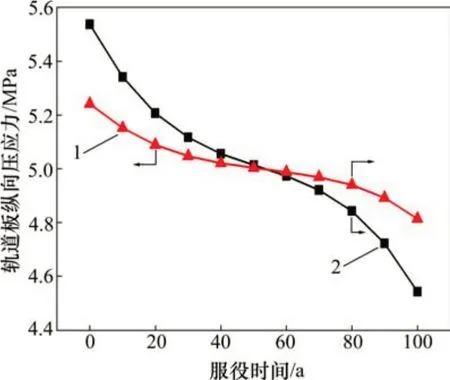
图5 正温度梯度作用下轨道板纵向压应力变化曲线Fig.5 Curves of longitudinal compressive stress of track plate under positive temperature gradient

CA砂浆与底座板的应力变化见表4。从表4可见：梁端处CA 砂浆压应力变化较跨中应力变化快，结构服役后期纵向压应力最大值出现在跨中位置，梁端压应力变化率为56.80%，跨中变化率为12.76%，可见CA砂浆在梁端处受力复杂，应力变化幅度较大，是结构易出现损伤破坏的位置。底座板应力同样不断减小，相比于CA 砂浆应力，其变化率较小。

3.1.2 结构各层变形分析

图6所示为轨道系统纵向位移变化曲线。从图6可见：每跨简支梁上轨道系统梁端1/4 跨范围内结构刚度退化较快，跨中范围内刚度变化较缓慢。在正梯度温度作用下，轨道系统受热膨胀使得中部结构在纵向上向两边延伸，因此，轨道系统的纵向位移变化可分为左右两侧，左侧位移随服役时间增加而继续向左移动，表现为位移减小，而结构右侧的位移刚好与之相反，位移改变速率明显可分为3个阶段。

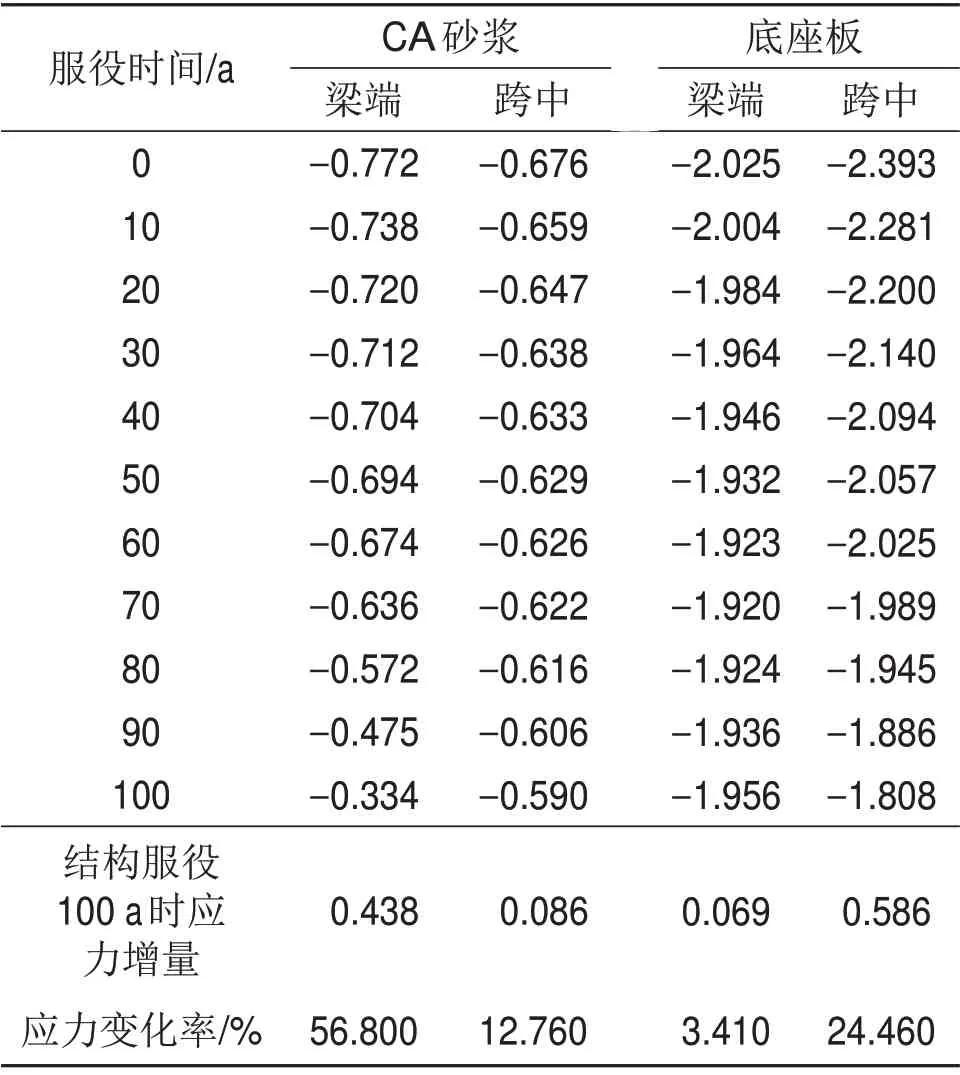
表4 CA砂浆与底座板不同服役期时的压应力Table 4 Compressive stress of CA mortar and base plate in different service periods MPa

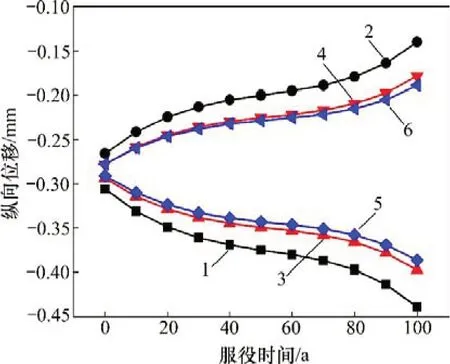
图6 正温度梯度作用下轨道系统纵向位移变化曲线Fig.6 Longitudinal displacement curves of track system under positive temperature gradient

图7所示为结构各层跨中位置竖向位移变化曲线。由于正温度梯度作用下结构将发生上拱变形，因此，结构产生向上的位移，轨道3层结构的位移相差不大，变化规律保持同步，仍遵循3阶段变化规律。从图7也可以明显看出结构体系服役80 a后，结构变形的速率显著增大。

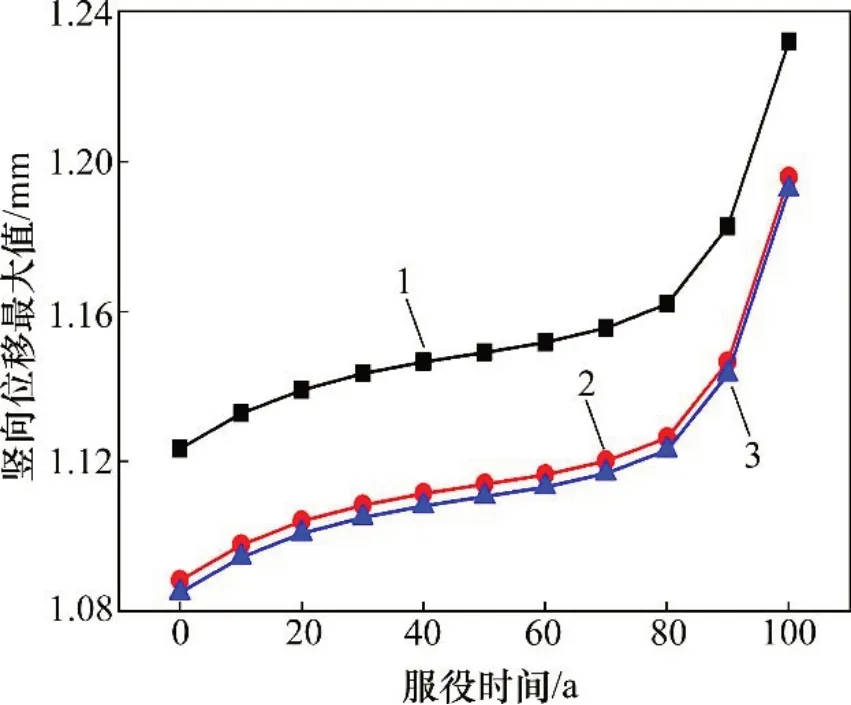
图7 正温度梯度作用下轨道系统竖向位移变化曲线Fig.7 Vertical displacement curve of track system under positive temperature gradient

3.2 整体降温作用下结构应力分析

轨道系统在整体降温下各层的应力变化见图8。从图8可见：轨道板在降温工况下，初始状态所受拉应力约10.79 MPa，在桥长范围内变化不大，超过轨道板材料C55 混凝土的抗拉强度3.3 MPa；而在轨道板的实际形状中其上表面存在假裂缝，在有限元计算分析中，通常认为在结构降温工况下，轨道板的假裂缝开裂，而不影响轨道板主体的横向断裂。故本文通过计算认为轨道板在降温工况下暂时不会开裂。

而CA砂浆的纵向拉应力在梁端处与其他各层有明显不同，其原因主要是简支梁梁端处受力较复杂，在结构体系服役的前60 a内，CA砂浆拉应力变化下降量很小，此后，该位置处的拉应力迅速减小，相应地，此处CA砂浆位移与相对位移迅速增大，轨道系统将面临损坏的可能。

本次研究表明，治疗组患者治疗后在心率、舒张压、收缩压水平等方面明显低于对照组，且治疗组在治疗过程中未出现肝脏和血液的毒副现象。这说明比索洛尔在降低患者心率及血压方面有显著效果，在治疗老年高血压伴心功能不全方面有积极作用，具有临床推广价值。

底座板纵向拉应力同样随服役时间的增加不断减小。不同之处是底座板跨中拉应力变化幅度较两端处拉应力变化幅度大，而轨道与CA砂浆在梁端处的拉应力变化幅度较跨中处的大。

3.3 单线列车荷载单独作用下结构受力分析

3.3.1 应力分析

单线列车荷载下轨道系统纵向应力变化曲线如图9所示。由图9可见：单线列车荷载作用下轨道板顶面的纵向应力有拉应力和压应力，有载侧轨道板在梁端转角处受拉，最大拉应力为0.56 MPa，跨中部分受压，最大压应力为0.28 MPa；无载侧最大拉应力为0.34 MPa，最大压应力为0.152 MPa；轨道板的拉压应力均随结构服役时间的增加有减小的趋势，有载侧的最大拉压应力减小量分别为0.08 MPa 和0.04 MPa，而无载侧的应力变化量很小，仅为0.004～0.008 MPa；对于应力变化速率，图9(a)中轨道板4个不同位置的应力变化曲线均可分为3阶变化阶段。

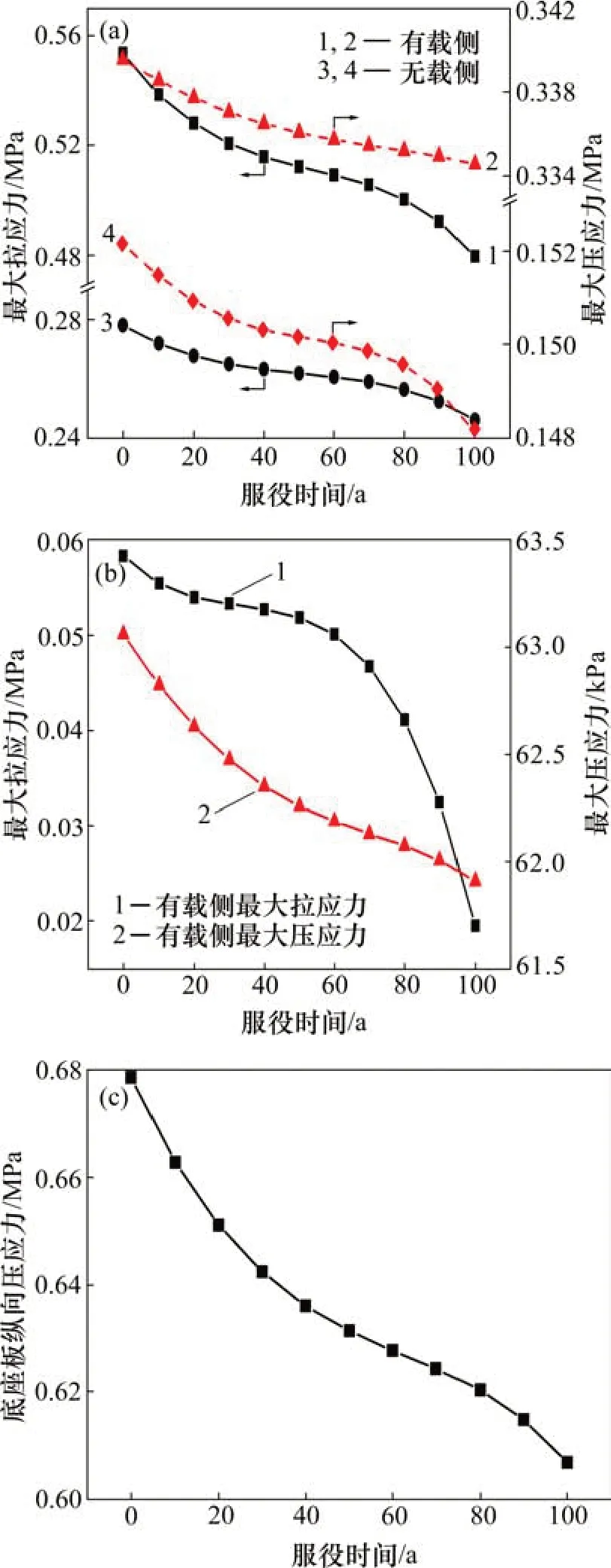
图9 单线列车荷载下轨道系统纵向应力变化曲线Fig.9 Longitudinal stress curve of track system under single train load

CA砂浆的纵向应力变化与轨道板的纵向应力变化较相似，梁端部分受拉，跨中部分受压，最大拉应力为0.060 MPa，最大压应力为0.063 MPa；最大拉应力随结构服役时间的变化量为0.040 MPa，变化率为67.67%；最大压应力同样减小，减小量为0.001 MPa，变化量很小。CA 砂浆的纵向应力随结构服役时间的变化曲线与其他工况下的曲线相似，在变化速率上与轨道板和底座板略有不同，仍呈3阶段变化，但第3阶段的开始时间提前至服役60 a时，此时CA砂浆的应力减小速率突然增大。

底座板的纵向应力与轨道板和CA砂浆的分布不同，底座板顶面以受压为主，跨中部分压应力较小几乎为0 MPa，并向桥梁梁端延伸逐渐增大，最大压应力为0.680 MPa；最大压应力不断减小，减小量为0.075 MPa，曲线3个阶段变化不太明显。

3.3.2 变形分析

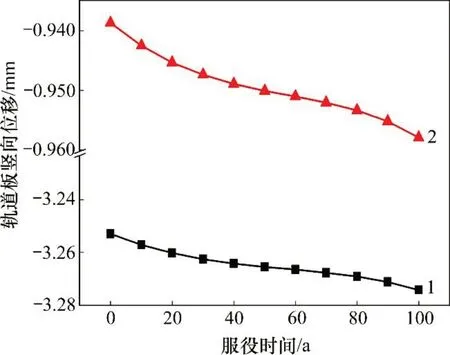
图10 单线列车荷载下轨道板竖向位移变化曲线Fig.10 Vertical displacement curve of track plate under single train load

3.4 列车荷载与整体降温作用下结构受力分析

3.4.1 应力分析

轨道板在结构服役初期有载侧与无载侧的应力相差不大，梁端拉应力稍大，跨中应力稍小，有载侧、无载侧最大拉应力分别为11.28 MPa 和11.04 MPa。随结构服役时间增加，结构拉应力不断减小，其中梁端处应力变化量最大，跨中处应力变化量最小。服役终态有载侧与无载侧轨道板的应力同样相差不大。由图11(a)也可看出梁端处应力变化曲线相互平行，跨中处应力变化曲线相互平行，且梁端处的应力变化量较跨中处大，4个不同位置的应力变化曲线均可分为3个阶段。

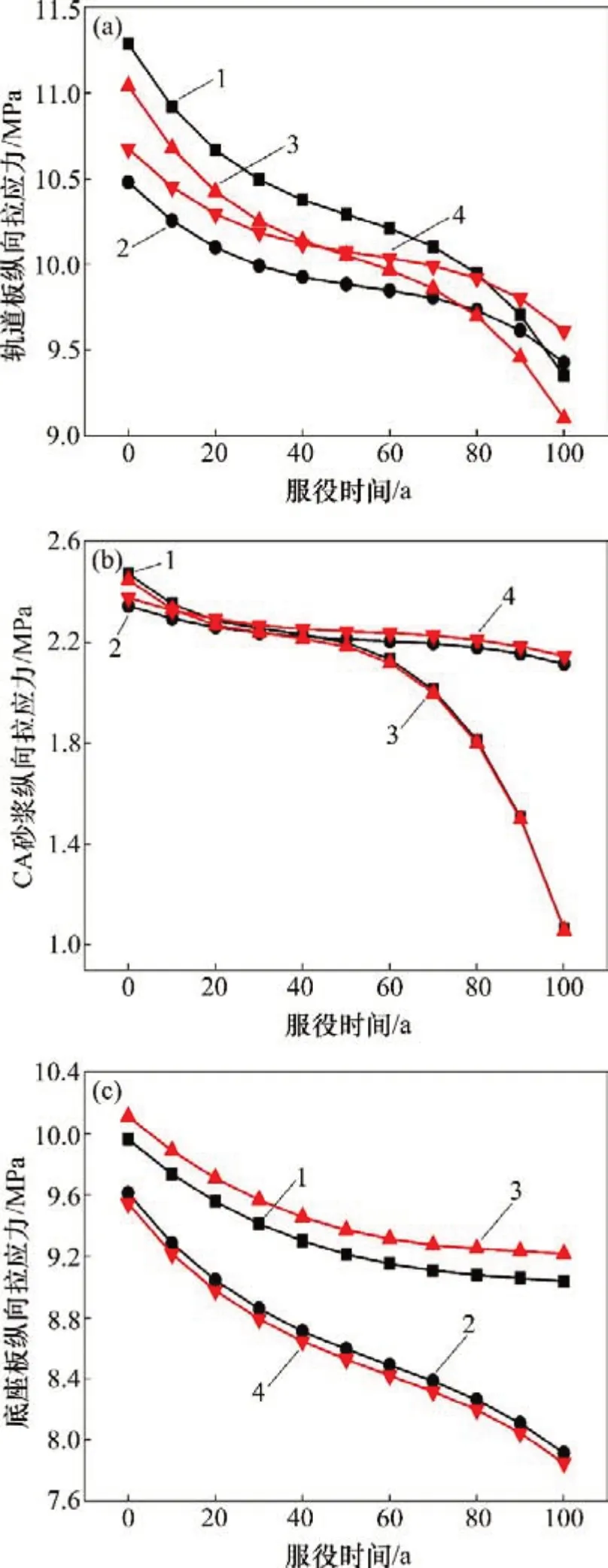
图11 荷载共同作用下轨道系统应力变化曲线Fig.11 Stress change curves of track system under multiple loads

CA砂浆的应力变化与轨道板应力变化稍有不同，有载侧与无载侧的应力几乎没有区别且随时间同步变化，梁端应力变化最大，跨中应力变化相对较小。在轨道系统的3 层结构中，CA 砂浆梁端处的应力变化率最大。由图11(b)可明显看出结构服役60 a后CA砂浆的应力快速变化，而跨中处应力仍按3个阶段缓慢减小。

底座板的应力与其他2层稍有不同，底座板跨中处应力变化比梁端处应力变化量大，跨中处应力仍按3 阶段曲线变化，梁端处应力变化稍有不同，先快速变化后趋于稳定。

对比分析3层结构的应力变化可知：结构体系在整体降温与列车竖向荷载共同作用下，各层结构在有载侧与无载的应力区别很小，说明温度作用比列车荷载对结构的影响大。对比结构整体降温作用时结构受力，在荷载共同作用下，结构的纵向应力仅有微小增大，可见荷载共同作用时单线列车荷载对结构应力变化的贡献几乎可以忽略。

3.4.2 变形分析

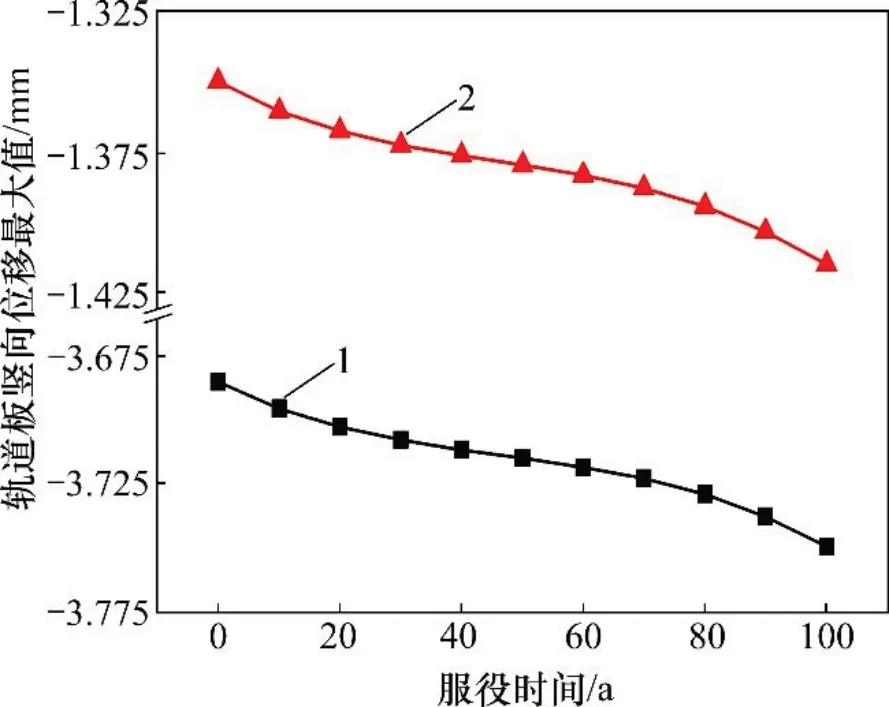
图12 荷载共同作用下轨道板竖向位移变化曲线Fig.12 Vertical displacement curves of track plate under multiple loads

经计算，结构体系在有载侧与无载侧的竖向位移差别较明显，有载侧钢轨的最大位移在集中力作用处的位移为-5.56 mm，轨道其他层的最大位移为-3.68 mm，无载侧最大位移仅-1.35 mm。图12所示为荷载共同作用下轨道板的竖向位移变化。从图12可见：竖向位移与其他有单线列车竖向荷载作用时的基本一致，竖向位移随结构刚度的退化稍有减小且减小变化曲线按变化速率均可分为3个阶段，两侧变化曲线保持平行，竖向位移增量相同。可见单线列车荷载的存在仅影响结构初始状态的变形，结构体系左右侧受力性能在刚度退化过程中的变化几乎保持同步。

4 结论

1)结构体系在正梯度温度作用与列车荷载单独作用下，轨道各层结构纵向以受压为主，在整体降温作用下，轨道各层结构纵向以受拉为主；随服役时间增加，轨道体统各层应力有所减小；结构各层的纵向位移在两侧1/4 位置处变化较敏感，随结构服役时间增加，纵向位移在1/4跨处不断增加或减小，竖向位移在跨中处最大且不断增大。

2)随结构服役时间增长，结构应力、位移变化较小，但在其变化曲线上可明显看出其变化速率多数可以分为3个阶段：第1阶段为结构服役初期的0～20 a，结构应力和位移变化较快；第2 阶段为结构服役20～80 a，结构应力和位移仍保持原来趋势但变化速率均匀缓慢；最后阶段为服役80～100 a，结构应力和位移再次快速增大。这与材料弹性模量下降曲线的3个阶段变化规律基本一致。而CA 砂浆层的纵向应力稍有不同，在服役60 a时应力将快速变化直至服役结束。

3)结构体系在整体降温与列车竖向荷载共同作用时，在同一个服役时间点，轨道系统在有载侧与无载侧的纵向应力相差不大，轨道系统的纵向应力随时间不断减小。结构体系在有载侧与无载侧的初始变形差别较大，单变化趋势始终保持同步。