基于区间二型模糊终端滑模控制的飞行器姿态控制*

马飞越，韩吉霞，牛 勃，佃松宜

0 引 言

四旋翼无人机具有垂直起降、操作灵活、控制方便、机动性高等优点[1-4]，因此被广泛应用在农业种植、林业资源调查、海洋巡检及城市航拍等诸多方面[5-8].四旋翼无人机系统为非线性动力学系统，本质是多变量的欠驱动系统[9]，其飞行控制系统是保障稳定飞行的核心，因此控制问题成为主要的技术难点.

近年来，许多学者提出不同的方法对四旋翼无人机进行控制.文献[10]提出传统PID的方法对无人机系统进行控制，设计结构简单，不依赖对象模型且参数整定有规律，但是系统的反映速度较慢且动态性能较差；传统模型预测的方法需要被控对象提供精确的数学模型[11]，但是抗干扰能力较差，当系统存在未知扰动时，效果较差；滑模控制对系统输入响应迅速[12]，且具有较好的鲁棒性，但存在抖振，不利于控制器的控制.

本文提出将区间二型模糊控制与非奇异终端滑模控制结合的方法.利用滑模的快速响应特性，令系统在有限时间快速收敛至平衡状态并抵抗干扰，通过设计区间二型模糊控制，增强对干扰的适应能力并再次提高系统的收敛速度且削弱抖振，使四旋翼系统拥有更加优良的飞行性能.

1 四旋翼动力学建模

1.1 坐标系定义

建立地面坐标系E(OeXeYeZe)和机体坐标系B(ObXbYbZb)，如图1.

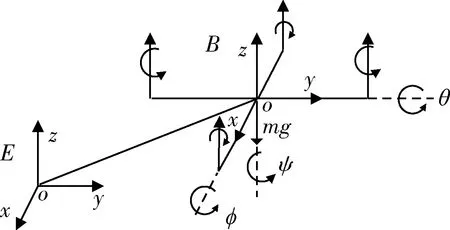
图1 地面坐标系与机体坐标系Fig.1 The ground coordinate system and the body coordinate system

定义地面坐标系原点为四旋翼起点，OeXe轴指向四旋翼飞行方向，OeZe轴垂直水平面向上，OeYe轴垂直OeXeZe平面且与其他两个坐标轴满足右手螺旋定则，OeXeYe平面为水平面.

定义机体坐标系的原点为四旋翼的质心，ObXb轴指向机体平面的正前方，ObZb轴垂直机体平面竖直向上，ObYb轴垂直ObXbZb平面且与其他两个坐标轴满足右手螺旋定则.

1.2 建立动力学模型

本文所设计的四旋翼飞行器在室内理想环境下进行姿态运动，飞行速度较小.建立其动力学数学模型时，可进行合理简化，假设：

1) 四旋翼飞行仿真器为刚体模型，结构均匀对称；

2) 当飞行器处于悬停状态，具有较小摄动时，其欧拉角(θ，φ，ψ)约等于转动角速度在机体坐标系中的投影(ωx,ωy,ωz);

3) 忽略空气阻力且不考虑旋翼的转动惯量；

4) 旋翼产生的升力与电机转速成正比；电机转速与电机电压成正比.

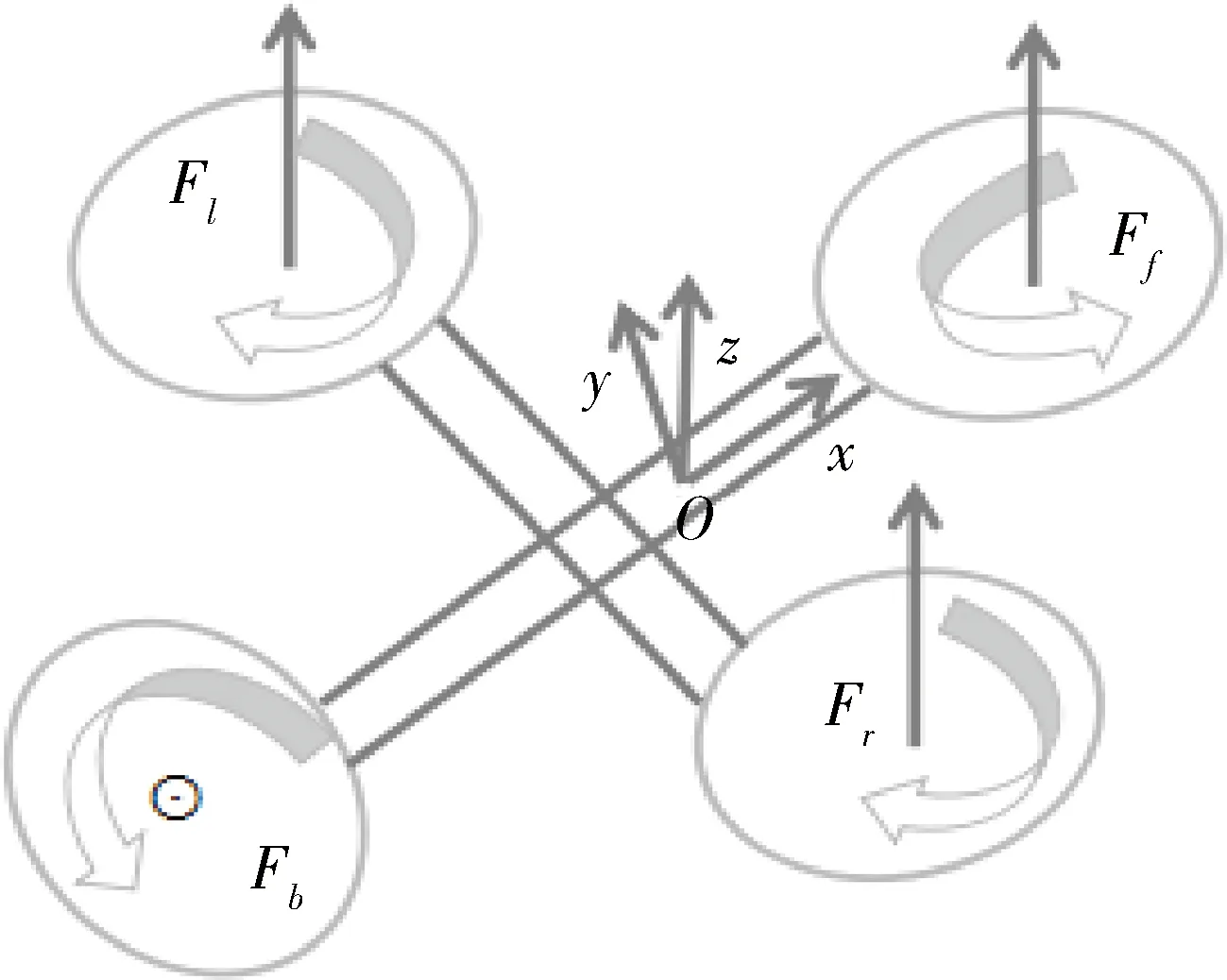
图2 四旋翼飞行器实验平台坐标系与受力分析Fig.2 Coordinate system and force analysis for experimental platform of four-rotor aircraft

四旋翼飞行器在某一时刻的姿态转动，可假设为其沿着该时刻角速度方向的瞬时转轴转动.转动方向随时间变化时刻改变，根据假设(1)，将四旋翼的姿态运动简化为刚体绕质心的定点运动.

四旋翼的机体坐标系沿机身惯性主轴，则取其惯性矩阵I为:

(1)

其中，Ix，Iy，Iz是四旋翼绕机体坐标系主轴的三个转动惯量.

飞行器对其质心角动量P表示为：

P=Pxi+Pyj+Pzk

(2)

其中，i,j，k为跟随刚体旋转的单位向量.

i,j，k与机体坐标系下转动角速度ω的关系如下：

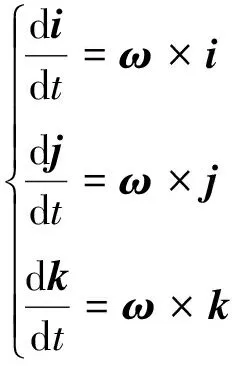
(3)

根据角动量定理，求得四旋翼系统综合力矩M为：

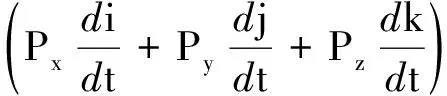
(4)

将式(3)代入到(4)中，得到：

(5)

将ω×P分解:

ω×P=(ωyPz-ωzPy)i+(ωzPx-ωxPz)j+

(ωxPy-ωyPx)k

(6)

将式(6)代入(5)中，得到角动量在机体坐标系的投影为:

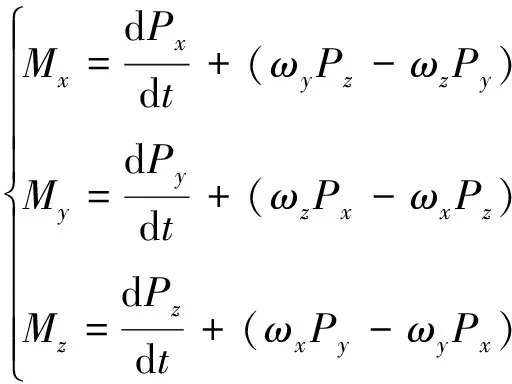
(7)

将(1)代入到(7)中，得到，

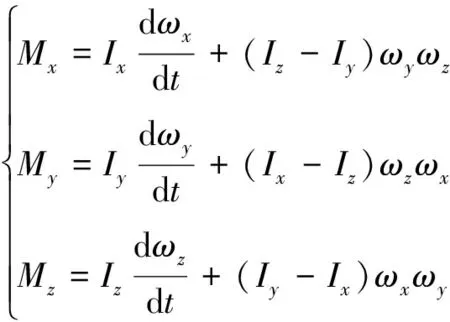
(8)

根据刚体绕定轴转动规律，建立俯仰角通道、滚动角通道及偏航角通道力矩平衡方程：

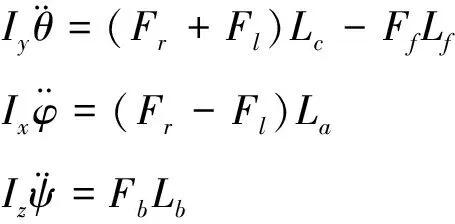
(9)

其中，Fr，Fl，Ff，Fb分别是四旋翼左侧、右侧以及前向、后向螺旋桨产生的升力.综合式(9)，将式(8)变为：

(10)

其中，Vr，Vl，Vf，Vb分别是四旋翼左侧、右侧以及前向、后向电机电压值，La，Lb，Lc分别为左右旋翼中心到Ox轴、Oy轴和Oz轴的力臂长，Kfa为旋翼电机电压与旋转升力相关系数.

根据假设式(2)，则式(10)可整理为:

(11)

所以，四旋翼动力学模型可表示为：

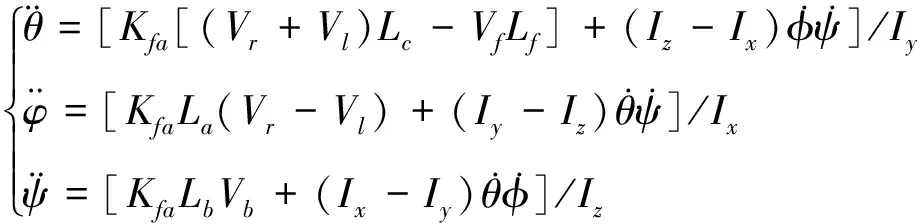
(12)

1.3 状态方程

X=[x1x2x3x4x5x6]T

(13)

其中：

(14)

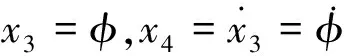
(15)

(16)

由式(11)可知，四旋翼俯仰角通道与滚动角通道存在耦合，而四旋翼前向电机与左右电机存在如下耦合关系[13]:

Vr+Vl=Vf

(17)

根据俯仰通道、滚动通道和偏航通道选择如下控制输入：

U=[u1u2u3]T

(18)

其中：

(19)

结合式(11)，(12)和(18)得到四旋翼系统的状态方程为：

(20)

2 非奇异终端滑模面设计

设俯仰角通道、滚动角通道以及偏航角通道的的理想输入信号分别为x1d,x3d,x5d,跟踪信号分别为x1,x3,x5.则可定义俯仰角、滚动角及偏航角跟踪误差为:

(21)

俯仰角速度、滚动角速度及偏航角速度跟踪误差:

(22)

其中，e1,e3，e5为俯仰角、滚动角及偏航角跟踪误差.e2,e4,e6为俯仰角速度、滚动角速度及偏航角速度跟踪误差.

为使俯仰角、滚动角及偏航角跟踪误差有限时间收敛，提高系统的跟踪速度，设计如下非奇异终端滑模面:

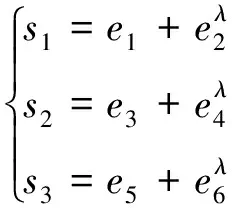
(23)

其中，λ=p/q,p,q均为正奇数，满足1

对滑模面求导，得到：

(24)

设计指数趋近律：

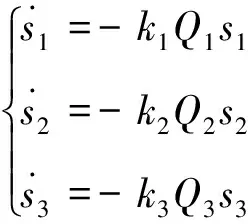
(25)

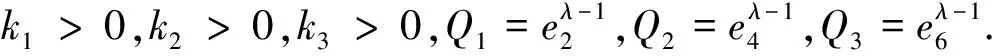
根据式(24)和(25)，可得控制律为：

(26)

3 区间二型模糊调节滑模趋近律

模糊控制是一种不依赖被控对象精确模型的无模型控制器，它对不确定性具有良好的处理能力.与一型模糊控制相比，二型模糊具有更好的对不确定性的处理能力.下面先介绍一些二型模糊控制的基本概念.

3.1 区间二型模糊控制器

通常，区间二型模糊控制器由五部分组成，即：模糊器、模糊推理机、规则库、降型器和解模糊器.如图3所示.

1) 模糊器：模糊器是区间二型模糊控制的前件，通过隶属函数将精确输入转成模糊输入.通常选择三角形函数、高斯型函数等作为上隶属函数(UMF)、下隶属函数(LMF).

2) 模糊规则：区间二型模糊的模糊规则可表示为：

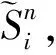
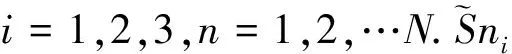
3) 模糊推理机：对于输入si和前件，点火区间Fn,表示为：

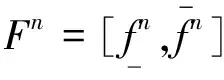
(27)

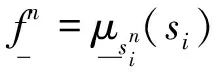
(28)

(29)

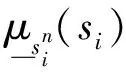
4) 降型器：本文选择集的中心法降型，表述为：

(30)

(31)

Ycos=[kl,kr]

(32)

5) 解模糊：通过解模糊，我们可得到最终输出，中心解模糊表示为：

(33)

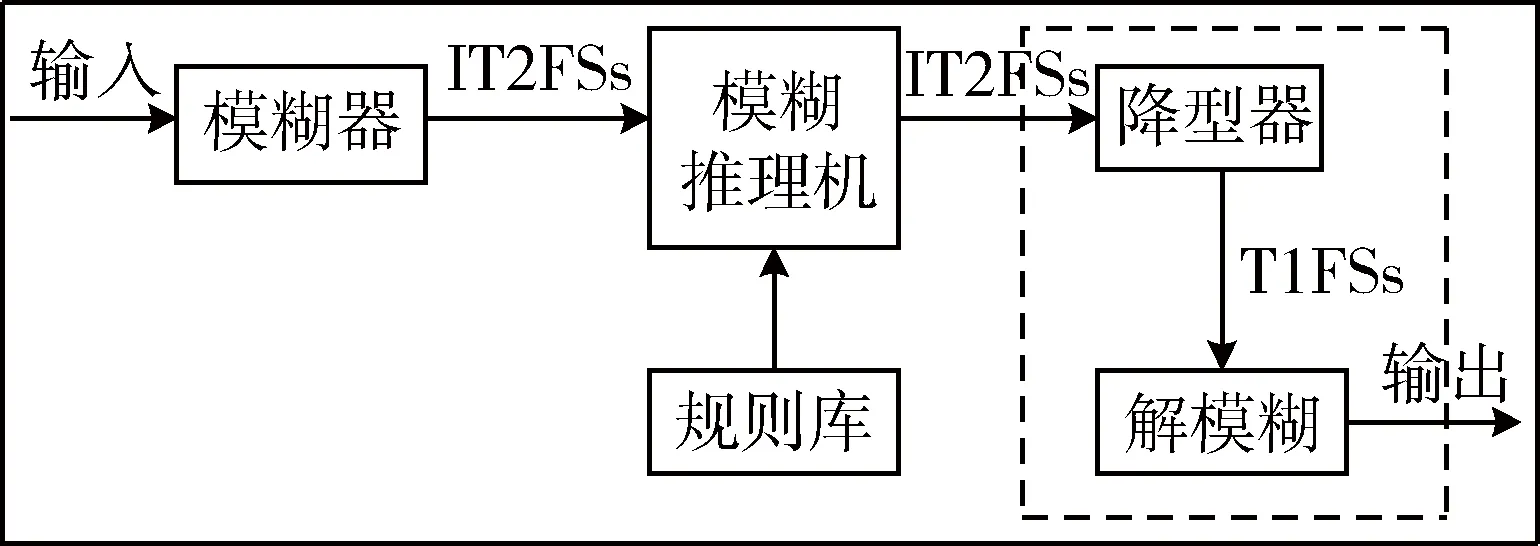
图3 区间二型模糊逻辑结构框图Fig.3 Structure diagram of interval type-2 fuzzy logic

3.2 IT2FLC调节趋近律

基于IT2FLC和NTSMC的四旋翼俯仰角、滚动角及偏航角角度跟踪框图如图4所示.

图4 基于IT2FLC和NTSMC的四旋翼俯仰角、滚动角及偏航角角度跟踪框图Fig.4 Tracking block diagrams of pitch angle, rolling angle and yaw angle of Four-rotor based on IT2FLC and NTSMC control methods

滑模控制因其变结构特性，具有很强鲁棒性，但参数的选择对其有较大影响.本文采用IT2FLC的方法动态调节滑模趋近律参数，使滑模具有更好的适应能力和抗干扰能力，在有限时间内快速收敛至平衡状态.

本文设计了三个模糊控制器分别控制俯仰角速度、滚动角速度及偏航角速度跟踪误差参数.模糊控制器输入分别为s1、s2和s3.输出变量分别为k1、k2和k3.模糊域分为四个模糊集IT2FSs，记为正大(PB), 正中(PM), 正小(PS)及零(ZR).上隶属函数和下隶属函数选择高斯型函数.

根据控制经验，当|s|>1时，应增大s1,s2,s3趋近律增益，让四旋翼俯仰角、滚动角及偏航角从初始位置快速趋近滑模面；当0<|s|<1时，应减小趋近律增益的值，降低四旋翼各角度趋近速度，削弱系统自身抖振.

IT2FLC规则表如表1所示.

表1 模糊控制规则Tab.1 Fuzzy control rules

4 仿真证明

本节的控制对象如式(12)，俯仰角、滚动角及偏航角控制律如式(26).取理想角度指令为：xid=sint,各角度的外部扰动为：d1=0.1×cost,位置初始值为：[0 0 0].为了更好显示本文方法(IT2FLC-NTSMC)的有效性，将本文方法与T1FLC(一型模糊控制)-NTSMC与NTSMC两种方法进行对比.仿真结果显示如图.

图5、6和7分别为外部扰动为d1=0.1×cost时的俯仰角、滚动角及偏航角角度跟踪情况.由图所示，本文采用的IT2FLC-NTSMC方法对理想角度具有最快最好的跟踪效果.

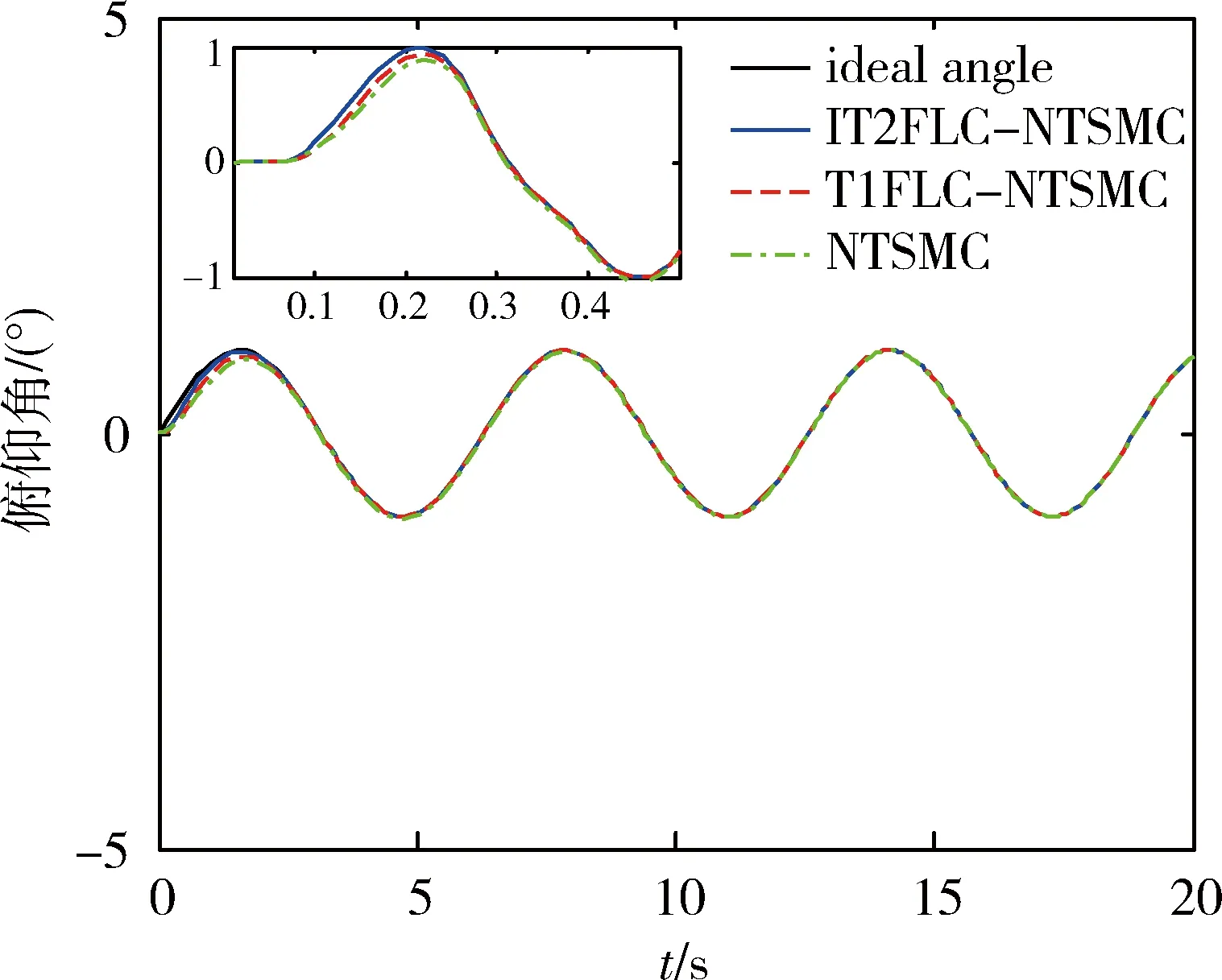
图5 外部扰动为d1=0.1×cost的俯仰角角度跟踪Fig.5 Pitch angle tracking with external disturbance of d1=0.1×cost

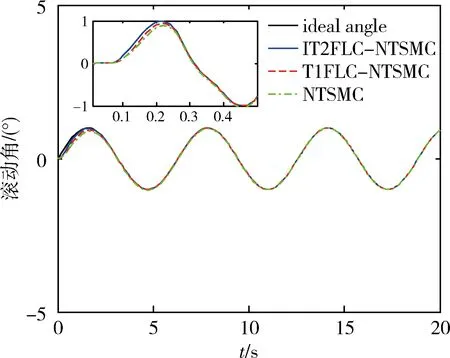
图6 外部扰动为d2=0.1×cost的滚动角角度跟踪Fig.6 Roll angle tracking with external disturbance of d2=0.1×cost

图7 外部扰动为d3=0.1×cost的偏航角角度跟踪Fig.7 Yaw angle tracking with external disturbance of d3=0.1×cost

图8、9和10分别为外部扰动为d1=0.1×cost时的俯仰角、滚动角及偏航角角度跟踪误差情况，如图跟踪效果显示的具有更加明显.本文提出的方法跟踪误差最小，且最快收敛至0.

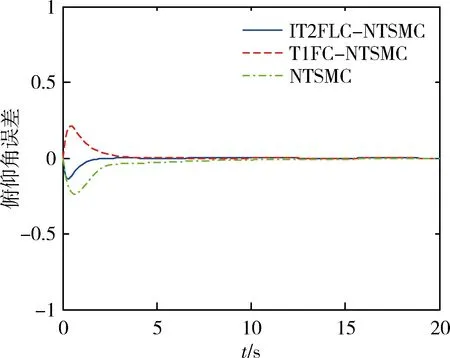
图8 外部扰动为d1=0.1×cost的俯仰角角度误差Fig.8 Pitch angle error with external disturbance of d1=0.1×cost

图9 外部扰动为d2=0.1×cost的滚动角角度误差Fig.9 Roll angle error with external disturbance of d2=0.1×cost

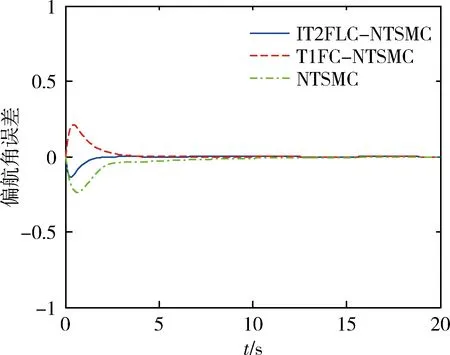
图10 外部扰动为d3=0.1×cost的偏航角角度误差Fig.10 Yaw angle error with external disturbance of d3=0.1×cost

图11、12和13分别为外部扰动为d1=0.1×cost时的俯仰角、滚动角及偏航角角度控制器.如图所示，本文提出的方法控制输入振荡最小，使四旋翼飞行器具有更加平稳的性能.

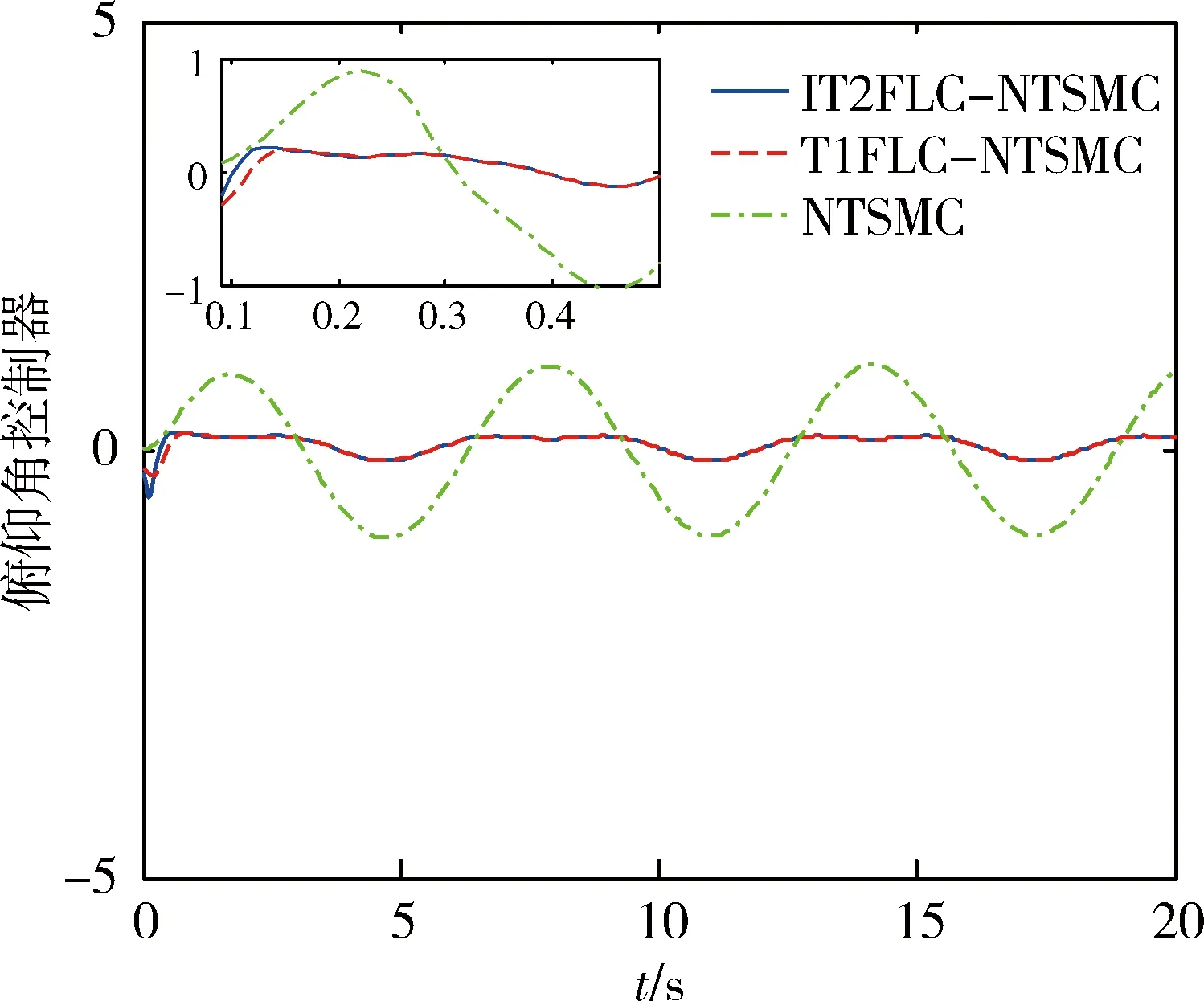
图11 外部扰动为d1=0.1×cost的俯仰角角度控制器Fig.11 Pitch angle controller with external disturbance of d1=0.1×cost

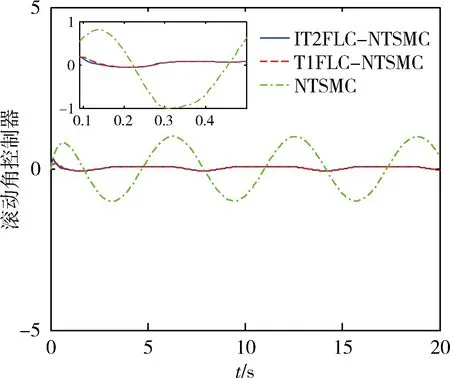
图12 外部扰动为d2=0.1×cost的滚动角角度控制器Fig.12 Pitch angle controller with external disturbance of d2=0.1×cost

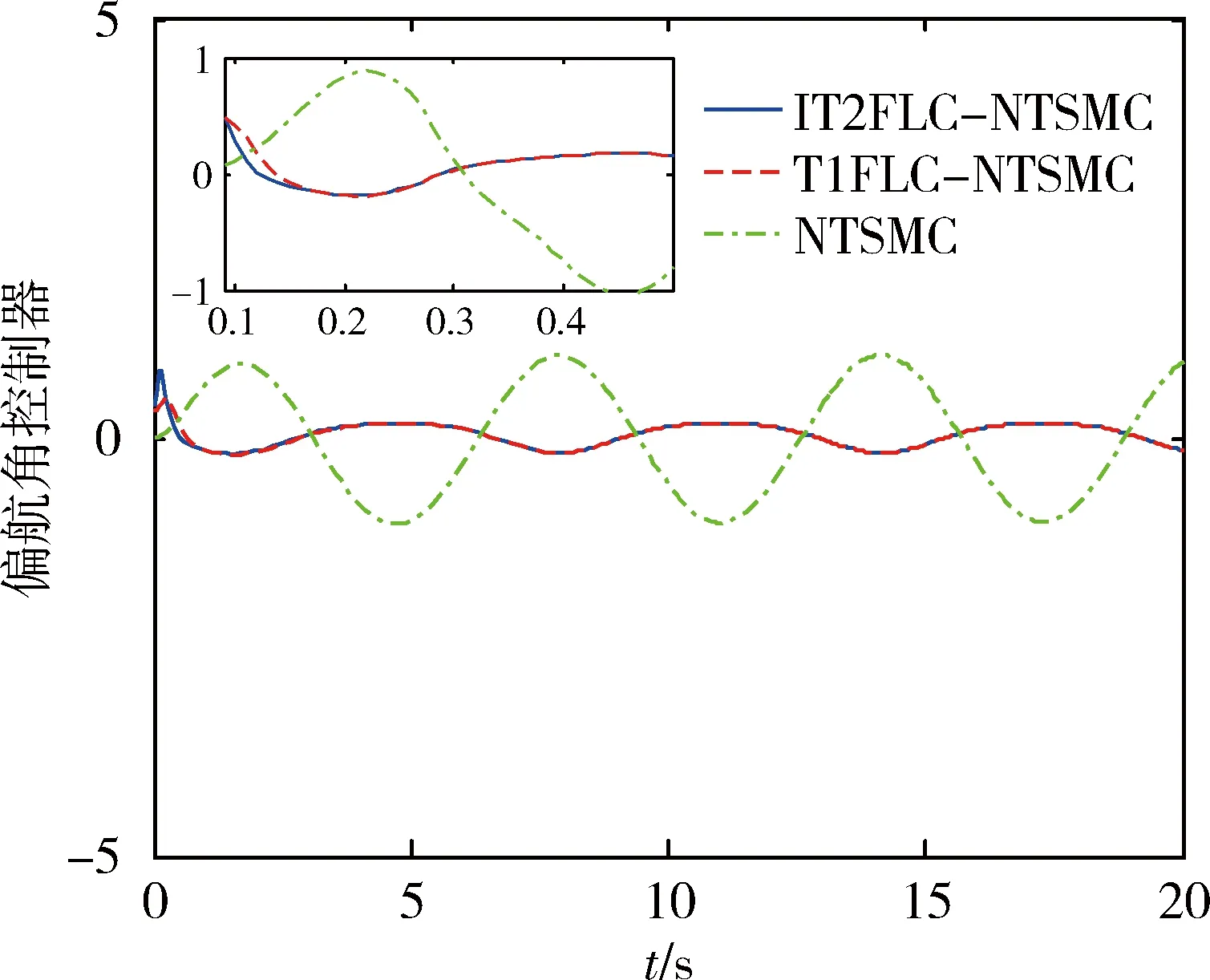
图13 外部扰动为d3=0.1×cost的偏航角角度控制器Fig.13 Yaw angle controller with external disturbance of d3=0.1×cost

5 结 论

本文提出了基于IT2FLC和NTSMC的四旋翼飞行器跟踪控制方法.俯仰角、滚动角及偏航角各设置一个控制器，均采用非奇异终端滑模控制的方法，利用滑模控制强鲁棒性，令系统在有限时间内快速收敛.采用IT2FLC控制器对各角度趋近律动态调节，加强对随机扰动的适应能力并削弱滑膜输入的抖振.最后，将本文提出的方法与T1FLC-NTSMC和NTSMC两种方法在四旋翼的跟踪效果上进行对比，仿真结果显示出本文所提出方法的有效性.