基于静电力平衡的石英挠性加速度计

张心悦，马官营，刘吉利，刘燕锋

0 引 言

加速度计作为敏感、测量运动物体加速度的传感器，是惯性测量和导航系统的主要惯性元件之一.随着航天技术的飞速发展，对加速度计的各项指标都提出了更高的要求[1-3].在电推进轨道转移过程中，卫星的加速度一般约为2～10 μg，考虑测量误差为推力的5%左右，则要求加速度计量程较小，分辨率需达到0.1 μg甚至更高[4-5].国内目前已有的石英挠性加速度计精度约为10 μg左右，不足以满足测量需求[6].针对提高石英挠性加速度计稳定性问题的研究，目前现有的方案大多是从对磁路稳定性的分析角度出发进行改进设计.文献[7]选择用剩磁和矫顽力温度系数小的磁钢材料来改善磁性能损失造成的磁场稳定性问题；文献[8-9]设计优化了磁路结构，使工作气隙磁场更均匀；文献[10]改进磁钢和磁极片的尺寸，改善了标度因数的时间稳定性.但由于磁场强度本身受温度、时间、环境磁场影响而发生非重复性变化，难以通过电磁屏蔽、温补等方式从根本上消除其不良影响，现有方案对于提高石英加计的稳定性仍存在很大的局限性.

针对上述问题，为了满足对空间加速度的测量需求，本文提出一种基于静电力平衡的新型石英挠性加速度计方案.采用静电力反馈，取代传统石英挠性加速度计中电磁力反馈的方式，实现闭环平衡控制.相较于电磁力，静电力不存在时间稳定性问题，且受温度影响相对小[11-12].此方案通过调节反馈电压大小可以改变反馈静电力强弱，提高了力反馈精度，以满足对小量程、高稳定性加速度计的空间应用需求.

1 工作原理

静电力平衡式加速度计系统结构主要由表头和控制系统组成.表头中摆片与上下极板构成两组差动电容器，加速度沿敏感轴输入使得摆片相对位置发生改变，从而引起电容值变化，经由电容检测电路检出，校正环节分析比较后产生反馈电压叠加到驱动电容上，利用电容产生的静电吸引力将摆片拉回到平衡位置.静电力平衡式石英加速度计系统结构如图1所示.

图1 静电力平衡式石英挠性加速度计系统结构图Fig.1 Structure of quartz flexible accelerometer system based on electrostatic force balance

图中，Vb为施加在摆片驱动电极上的恒定直流电压；Vf为力平衡反馈电压，施加在差分驱动电极上的力平衡反馈电压大小相等，方向相反；Cs1，Cs2为检测差动电容器;Cd1，Cd2为驱动差动电容器.

2 表头结构

静电力平衡式石英挠性加速度计表头结构主要由表芯、密封盖、密封环部件、抽气嘴、壳体以及底座等部分组成.

将加速度计表头结构简化后的示意图如图2所示.

其中，表芯部分为“三明治”式结构，由敏感摆片和一对固定电极板构成.摆片采用的是熔融石英材料，是由整块熔融石英平板加工形成的挠性敏感元件，摆片与上下极板间通过安装螺母螺钉进行组装，摆片可动部分(摆舌)即在两极板间隙活动.摆片上镀有金属镀层，两个固定电极板的镀层的位置以及尺寸上与摆片相对应，分别组成圆形结构的差分检测电极和圆环结构的驱动电极.

图2 静电力平衡式石英挠性加速度计表头示意图Fig.2 Diagram of quartz flexible accelerometer header based on electrostaic force balance

表芯部分安装于底座上，采用了单端引线的方式进行信号传输，由密封环部件上引出接线柱，与上极板引线对应连接.抽气嘴用于对表头进行抽真空处理，抽气嘴与密封盖之间进行锡焊连接，壳体与底座、壳体与密封环、密封环与密封盖之间通过激光焊接的方式进行连接.

上述基于静电力平衡的石英加速度计表头结构简单，采用差分电容替代传统石英加速度计的磁体和线圈，在一定程度上降低了结构的复杂程度.同时，为了降低机械热噪声对于加速度计表头的影响，采取对表头进行抽真空处理的方式，令表头阻尼近似为0.整个表头结构除表面镀层外全部采用石英材料，有助于提高加速度计的稳定性.

3 控制系统设计

3.1 总体方案

静电力平衡式石英挠性加速度计的控制系统主要包括电容检测电路、阻尼补偿、校正以及低通滤波等环节.基于新型加速度计表头为被控对象，建立闭环控制反馈回路，控制系统和表头之间的信号转换关系情况如图3所示.

图中，Vs为电容检测电路输出电信号，Mf为再平衡反馈力矩.

3.2 表头模型

表头作为加速度计控制系统的被控对象，是整个闭环控制系统设计分析的基础，因此需要首先进行表头模型的建立.设测量加速度为a，摆片转动角度为θ，敏感摆片的动力学微分方程为：

(1)

式中，设摆片质量为m，摆片质心距离(相对悬臂梁固定端)为L，则摆性P=mL；J为摆片的转动惯量；Kh为摆片的转动刚度，其中，刚度仅考虑了机械刚度，暂未考虑静电力负刚度；δ为摆片的转动阻尼，当表头处于高真空度时，δ≈0.

则表头系统的传递函数即为：

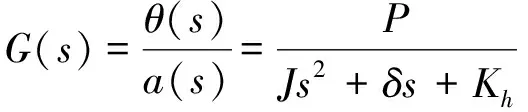
(2)

图3 加速度计控制系统与表头之间信号转换关系图Fig.3 Signal conversion diagram between accelerometer control system and header

3.3 控制系统参数设计

当有加速度输入时，摆片发生摆动，其相对上下两固定极板间距发生改变，两个检测电容器出现电容差值.由于摆片上不同位置处电容间隙变化不均匀，所以电容值大小也不等，产生的电容变化量也不相同.因此，检测电容值实际大小需通过积分计算得到.由图2知检测电极板形状设计为圆形，设检测电极板半径为r,介电常数为ε,检测电极相对极板面积为As,初始间隙为d0,以摆片位于平衡位置时的质心为原点建立直角坐标系，如图4所示.

当摆片位于平衡位置时，初始检测电容大小相等，即：

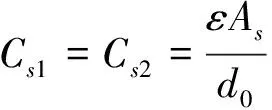
(3)

当摆片如图4所示相对平衡位置摆动一个角度θ,设摆片上相对质心距离为x位置处在y轴方向上的位移为Δd，则：

(4)

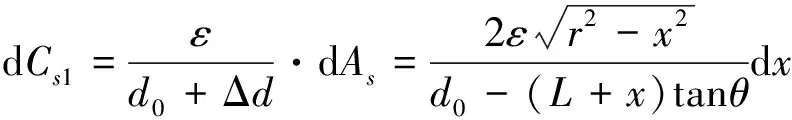
(5)

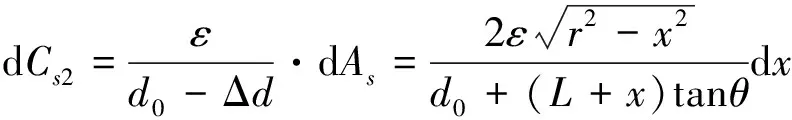
(6)

dΔC=d(Cs1-Cs2)=

(7)

对式(7)在(-r,r)上进行积分运算，即得到检测电容变化量：

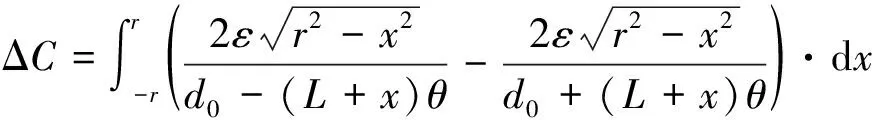
(8)

对式(8)的积分进行运算处理，将结果以图像化形式呈现，得到ΔC与θ关系特性曲线如图5所示.

图4 摆片位置状态示意图Fig.4 Diagram of pendulum state

图5 差动检测电容变化量与摆动角度关系Fig.5 Variations of static capacitance change and pendulum angle

对上述仿真曲线在θ为零值附近进行线性拟合，拟合曲线如图中红线所示.可以看出，当转动角度很小时，检测电容的变化量ΔC与摆动角度θ之间可以近似成线性关系.

根据前文所述的静电力平衡石英加速度计工作原理可知，加速度计一般工作在力平衡闭环条件下，摆片受再平衡力矩的作用始终工作在平衡位置附近，摆片转动角度非常小，因此，加速度计摆片的摆角θ与检测电容变化量ΔC可以成比例关系进行转换，其二者存在关系：

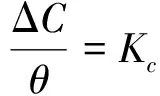
(9)

其中，Kc为常数.

电容检测电路采用环形二极管电容检测电路[13]，在闭环系统中将电容变化量转换为电压信号，并进行比例放大后输出.分析可知，输出电压信号Vs与ΔC存在非线性关系,在ΔC=0处将其简化为线性模型：

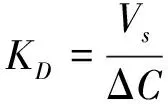
(10)

则由式(9)和(10)可以得到检测电路的输出电压信号Vs和摆角θ之间存在关系：

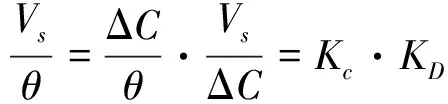
(11)

加速度计采用差分式电容驱动，设驱动电容的相对极板面积为Ad,根据图2表头结构可知，驱动电极与检测电极初始间隙相同，则在平衡位置处的初始驱动电容值为：

(12)

当摆片状态如图4所示，施加在驱动电容极板上的反馈电压大小相等，方向相反，反馈电压产生的等效平衡力矩作用于摆片，将摆片控制回平衡位置.设电容器Cd1，Cd2电容存储能量分别为W1和W2,对摆片产生的静电驱动力矩分别为M1和M2,表头结构中驱动电极为圆环，内环半径为检测电极圆面半径r,设外环半径为R,则：

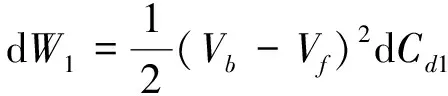
(13)

其中，

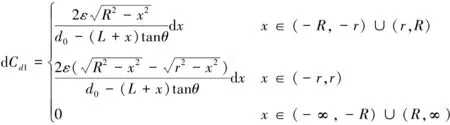
(14)

将式(14)代入式(13)中，得到：

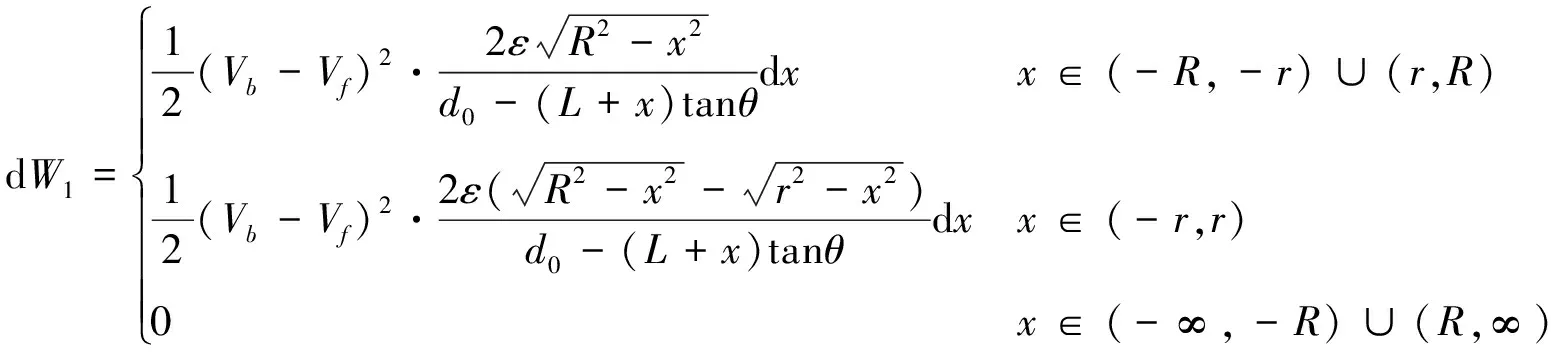
(15)

进而可以得到：

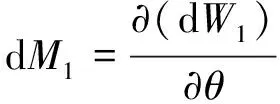
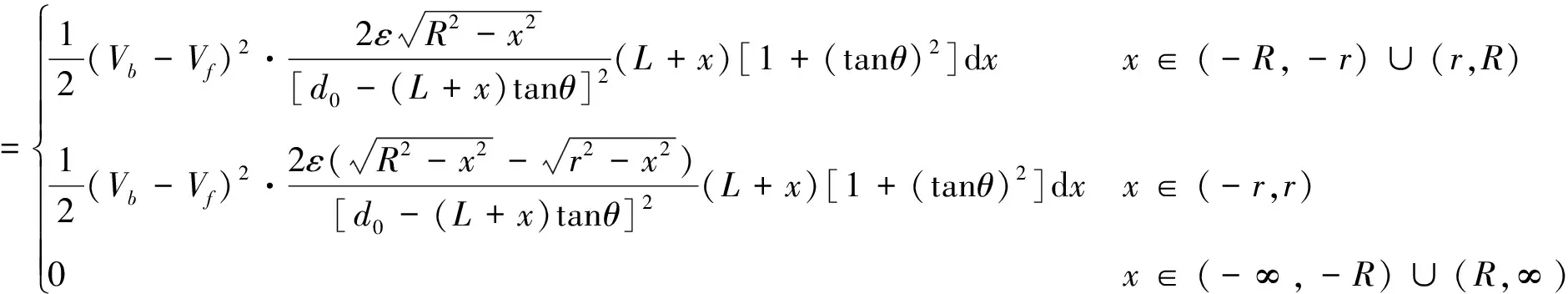
(16)

则得到电容器Cd1产生的静电驱动力矩：

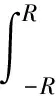
(17)

同理可以得到M2，则摆片受到的等效平衡力矩为：Me=M1+M2，由于摆片始终工作在平衡位置附近，所以在θ近似为0条件下，将等效平衡力矩线性化，得到反馈电压与平衡力矩之间的关系曲线如图6所示.

图6 反馈电压与静电平衡力矩关系曲线Fig.6 The relationship curve between feedback voltage and electrostatic balance torque

4 控制系统仿真分析

基于3.1中对控制系统结构的各变量之间的转化分析，建立静电力平衡式石英加速度计闭环控制系统的结构框图如图7所示.

图中，闭环控制系统由一个内环回路和一个外环回路构成，内环回路加入电阻尼环节作为高真空度表头的等效阻尼项，在此基础上，设计校正网络与内环回路组成加速度计控制系统的闭环结构.

由表头结构知，静电力平衡式石英加速度计表头为高真空状态，空气阻尼δ近似为0，则敏感摆片的传递函数由式(2)可改写为：

(18)

表头在低频处会出现振荡特性，其幅频特性曲线如图8所示.

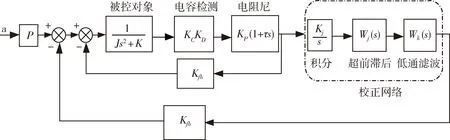
图7 闭环控制系统结构原理图Fig.7 Structure schematic diagram of closed-loop control system

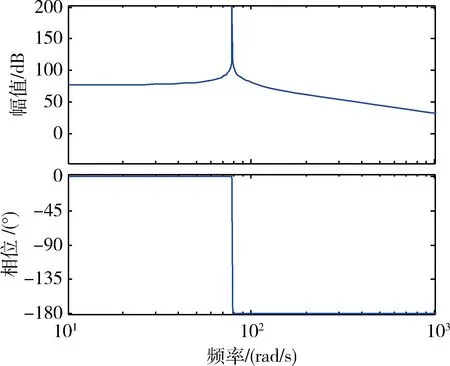
图8 高真空度表头振荡特性Fig.8 Oscillation characteristics of high vacuum gauge head

低频振荡会对整个系统的稳定性造成非常不利的影响，由于振荡频率在所要求的带宽以内且易受环境等因素而变化，采用常规的零极点对消的方式难以解决.因此，在闭环控制系统中引入电阻尼补偿环节，避免系统在谐振频率处振荡.在控制电路中增设一个含有比例微分环节的内环回路，KP(1+τs)作为等效的阻尼项，加入电阻尼后，内环回路等效传递函数为：

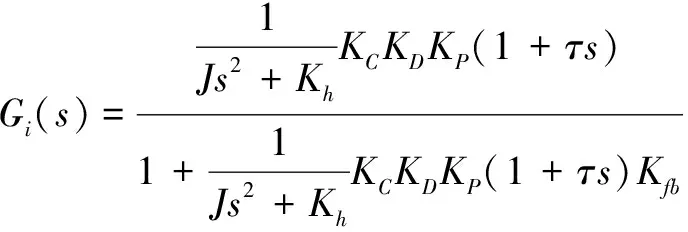
(19)

内环回路的幅频特性曲线如图9所示.加入电阻尼后可以看到避免了上述表头在谐振频率处震荡的现象，其幅频特性得到明显改善.

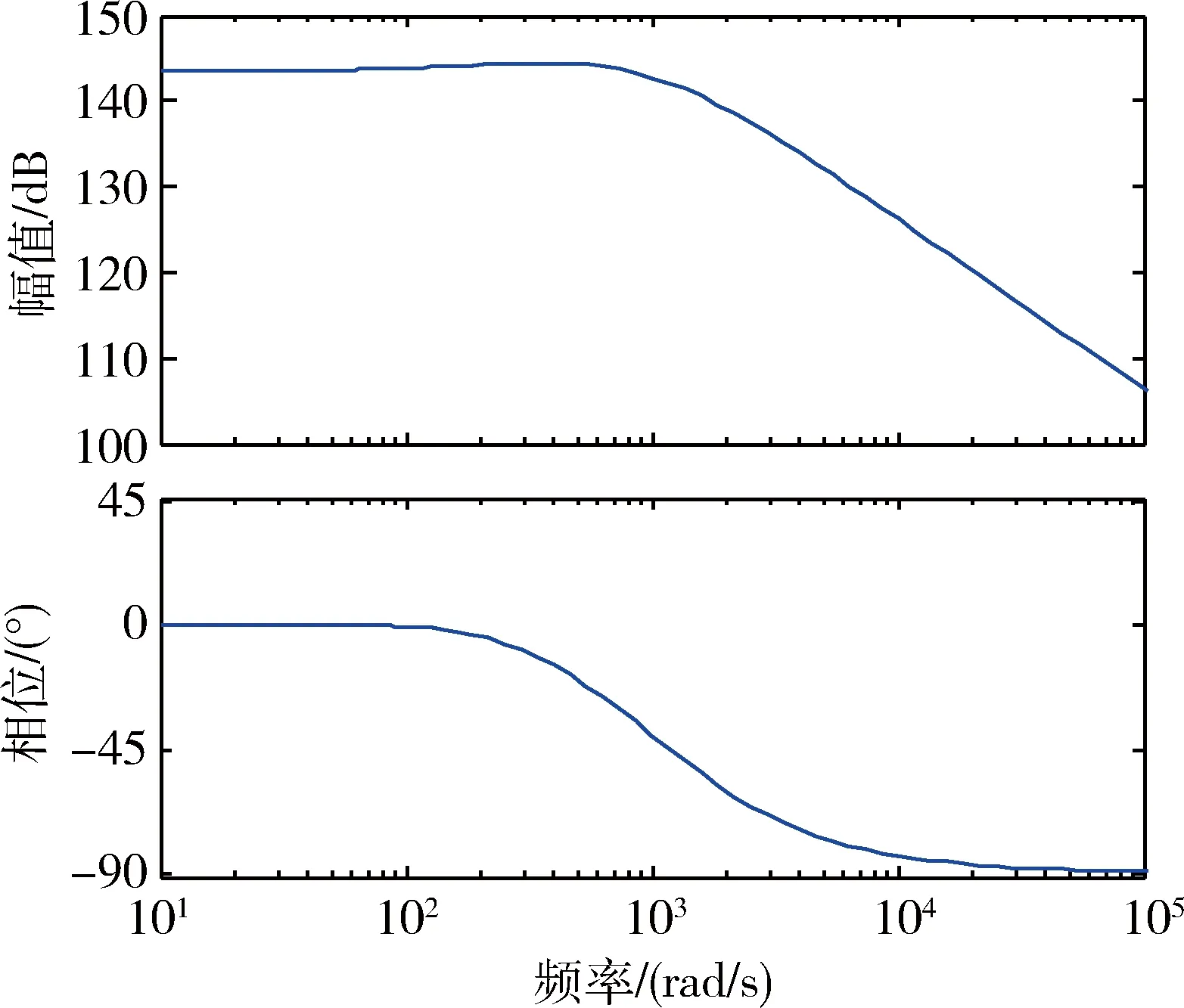
图9 加入电阻尼后系统幅频特性曲线Fig.9 Amplitude-frequency curve of system after adding resistor

由式(19)可知，Gi(s)是0型系统，当闭环系统输入阶跃信号，即u(t)=c·1(t)时，系统存在一阶静态误差，闭环系统的稳态误差为：

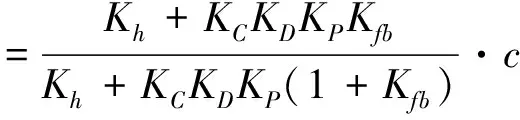
(20)

将表头的实际相关参数代入，选取Kj=1,在此基础上，设计了基于PID控制的超前滞后校正环节Wj(s),使系统具有更加优良的动态性能.同时，在闭环回路中加入低通滤波环节Wk(s),经过多次的计算及仿真，确定其表达式如下：

(21)

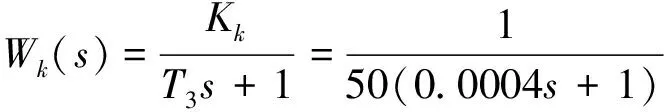
(22)

得到校正后的系统开环传递函数：

G0(s)=G01(s)·Wj(s)·Wk(s)·Kfb

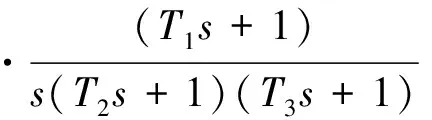
(23)

校正后的系统开环幅频特性曲线如图10所示.

图10 校正后的开环幅频特性曲线Fig.10 Open-loop amplitude-frequency characteristic curve of corrected system

从图10可以得到加入校正环节后系统的剪切频率为7.58×103rad/s，相角裕度约为89.3°，满足系统稳定性条件.加速度计系统带宽为267 Hz，闭环系统的单位阶跃响应如图11所示，得到系统的超调量为4.6%，调节时间为5 ms.当输入加速度为1 g，输出电压为75.5 V.

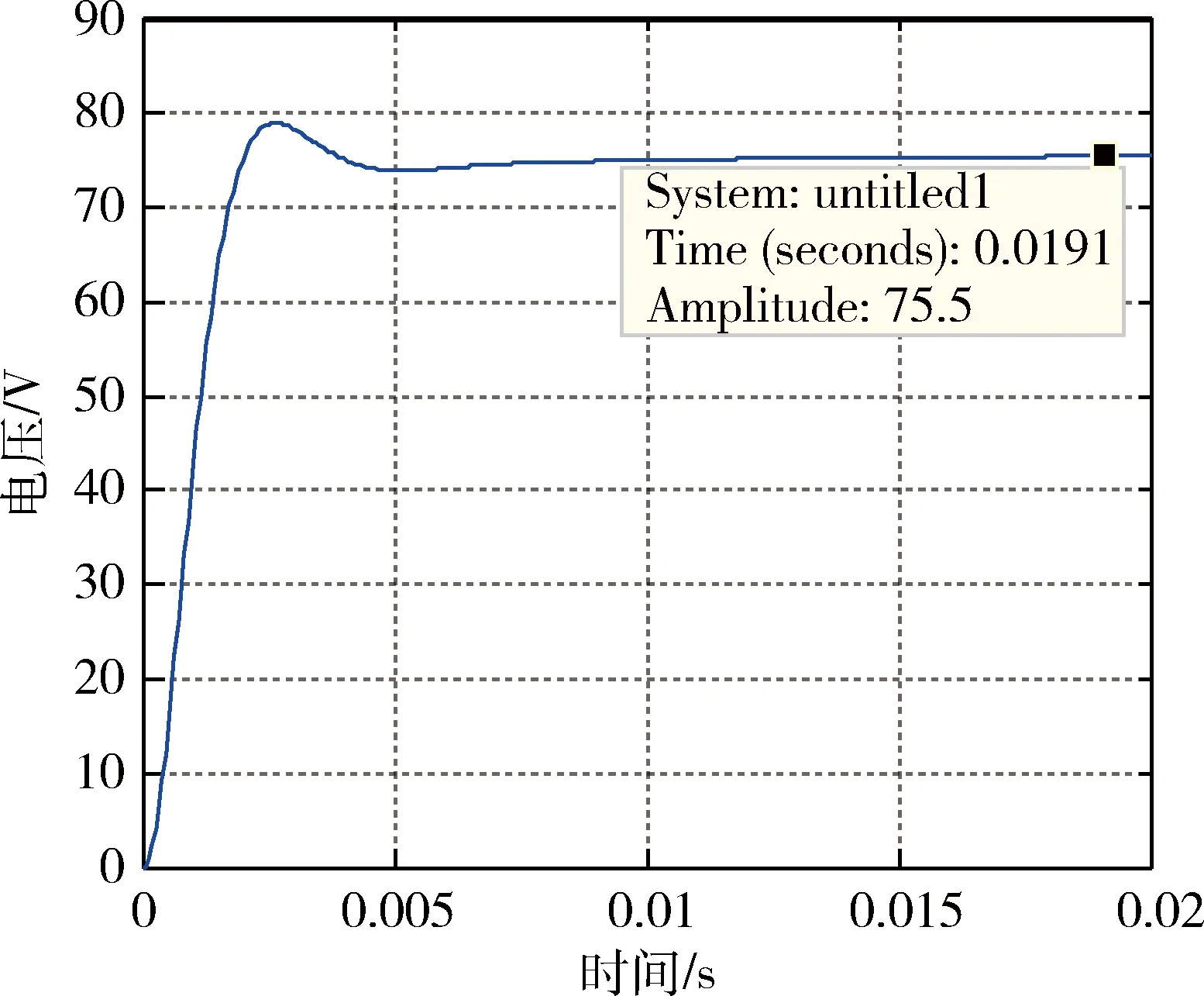
图11 系统阶跃响应曲线Fig.11 step response of system

5 测试验证

5.1 测试系统组成及测试方法

本文选用实验室的分度头作为实验平台对静电力平衡式加速度计进行性能测试，测试系统主要包括分度头、万用表、安装夹具、阻容测试仪、示波器、加速度计工作和测量时所需的交、直流电源设备等.

将加速度计通过卡具安装在分度头的转盘台上，令加速度计的输入轴平行于铅垂平面为初始状态，并与运算放大电路及控制电路板对应接口正确连接.如图12所示.通过手柄改变输入加速度值的大小，观察对应输出电压的变化.

图12 加速度计测试系统Fig.12 Accelerometer testing system

5.2 测试内容及结果

5.2.1 量程和标度因数测定

通过分度头旋转不同的角度使加速度计敏感不同的重力加速度,不同的加速度输入，得到对应的输出电压值.根据表头结构的实际参数，得到输出饱和电压值为±10 V左右.在此范围内，每间隔约90 s改变一次输入的加速度大小，共取得15组输出电压信号数据.将得到的电压数值与对应输入加速度进行一次曲线拟合，得到其二者之间呈线性关系，如图13所示.得到加速度计的量程可以达±0.12g，标度因数为75.56 V/g，与前文中闭环系统的时域仿真结果一致.

图13 输出电压与输入加速度的关系Fig.13 The relationship between output voltage and input acceleration

5.2.2 零偏稳定性测定

通过对稳定后的加速度计进行静态性能指标测试，标定出加速度计的零偏稳定性.零偏稳定性是指在无加速度输入的情况下，加速度计输出量围绕其均值的离散程度.在规定时间内，零偏稳定性采用算法如式(24).

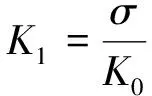
(24)

式中，K0为标度因数，σ为标准方差，K1为零偏稳定性.

新型加速度计在正常试验条件下，对输出电压数据进行采集，平均大约每4 s钟测得一个点数据，共测得近6000余组电压输出值，计算得出加速度计在此实验时间每1小时的标准方差，共7组数据，根据式(24)，结合前文中计算出的标度因数结果，得到静电力平衡式加速度计的零偏稳定性测试结果如表1所示.

表1 加速度计零偏测试结果Tab.1 Accelerometer bias test results

根据表1中测得结果可以得到此新型石英加速度计的零偏稳定性约为1.51 μg.与目前现有石英加速度计的零偏稳定性指标相比，水平有所提高，多次测量结果表明基于静电力平衡的闭环力反馈结构具有较高的稳定性，在一定程度上有效提高了石英加速度计的精度水平.

6 结 论

本文针对小量程、高精度的加速度计空间应用需求，设计了一种基于静电平衡式的新型石英加速度计.建立了加速度计的表头结构模型和摆片数学模型，基于对各变量转换关系分析，设计了基于静电力作为反馈要素的闭环控制系统，并对该控制系统进行了仿真分析.同时以高精密分度头作为实验平台，测得新型加速度计样机的量程为±0.12g，零偏稳定性约为1.51 μg.实验证明了本文提出的静电力平衡式加速度计结构的正确性和有效性，也为今后工程应用提供了理论依据.而所提出的静电力平衡式结构尚未充分考虑到温度、气流扰动等对控制系统稳定性的影响，下一步工作将在此基础上考虑加入温控等环节，从而进一步提高表头结构的稳定性.