有限域子集上的Hermite 判别法及推广
郭 异,张起帆
(四川大学数学学院,四川 成都610064)
在数论研究中,关于有限域的研究占据了相当重要的地位.有限域在现代数学及计算机科学的多个领域都有着重要的应用.令Fq为q 元有限域,其中q=pr,我们自然对Fq上的函数及其性质感兴趣.特别地,对Fq上的双射函数,自19 世纪以来,已有学者进行了大量研究,重要的成果包括Hermite[1],Dickson[2],Cohen[3],Wan[4],Turnwald[5]及Zieve[6-7].
尽管关于有限域Fq上的双射已有不少重要成果,关于有限域Fq上子集的函数却缺少相关研究.本文研究重点将集中于有限域Fq上子集,通过引入有限生成代数的观点,说明对于有限域Fq上子集也有类似有限域上Hermite 判别法的结论成立,且可将一些基于有限域Fq上Hermite 判别法的研究成果平行地推广到子集上.
1 相关背景回顾
本节主要回顾本文将会用到的已有研究成果与结论.由于任意一个Fq到Fq上的函数,都可唯一表示为Fq上次数小于q 的多项式g,对于有限域上的双射函数自然转化为对置换多项式的研究.置换多项式的研究已有相当长的历史.这一方面的早期结果,参见Lidl and Niederreiter[8].

定理1.1 (Hermite 判别法)
由于对有限域Fq,有正交性:
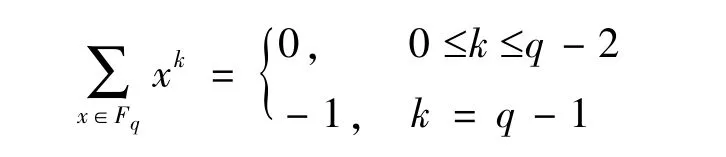
因此,对Fq上多项式g(X),由gmod Xq-X 的q-1 次项决定.进而,对k ≤q-2,f 满足前k个Hermite 条件等价于fkmod Xq-X 的次数小于q-1,即有常见版本的Hermite 判别法:
定理1.2 (Hermite 判别法,经典形式)
f(X)是置换多项式⇔下列两个条件成立:
1)f(X)在Fq中恰有一个零点.
2)fkmod Xq-X 的次数小于q-1,其中1 ≤k ≤q-2.
置换多项式,虽然定义简单,但却难于研究.为此,人们引入了例外多项式的概念来帮助研究置换多项式.例外多项式(最早由Davenport and Lewis[9]提出),基于几何性质定义,更易通过较为深刻的几何工具来帮助研究;基于Lang-Weil 估计[10]可知,次数远小于q 的置换多项式均为例外多项式.另一方面,由Davenport and Lewis[9]猜测,并由S.D.Cohen[3]证明了下列重要定理:
定理1.3 (Cohen,1970) Fq上例外多项式都是置换多项式.
进一步的,M.Zieve 等人[6-7]于2010 年几乎完全刻画了有限域上例外多项式,取得了对有限域上置换多项式的结构刻画的重大进展.
S.D.Cohen[3]给出的证明大量利用了群论工具,这使得证明稍显复杂.其后多人改进/拓展了这个证明,下面列举一些有代表性的相关成果:
K.S.Williams[11-12]利用Newton 公式,对大特征情形给出了一个非常简洁的证明.他得到:
定理1.4(Williams,1968). 有限域Fq上多项式f(X)是置换多项式,当且仅当存在正整数m <p,使得
1)f 满足前m 个Hermite 条件.
推论1.5 有限域Fq上多项式f(X)是置换多项式,如果存在正整数m <p,使得
等价地,有
等价描述若有限域Fq上次数为d 的多项式f(x)不是置换多项式,那么对任意满足的正整数m,f 的值集大小.特别地,f 有值集大小上界
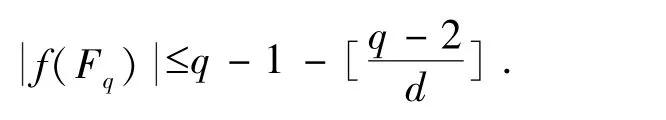
这个上界对于q=p 的情况相当好,但对于一般情形,Newton 公式可能失效,因而不适用于小特征情形.1991 年,万大庆[4]注意到推论1.5 中条件(1)包含了比定理1.4 中更多的信息.充分利用这个条件,万大庆成功将Williams 的证明提升到了Newton 公式适用的p-adic 数域上,从而克服了小特征障碍,给出了Cohen 定理的一个新的完整证明.事实上,他得到了以下结论:
定理1.6(Wan) 有限域Fq上多项式f(X)是置换多项式,如果存在正整数m,使得
等价地,我们有
等价描述若有限域Fq上次数为d 的多项式f(X)不是置换多项式,那么对任意满足的正整数m,f 的值集大小.特别地,f 有值集大小上界

最近,张起帆利用线性代数理论推广了Hermite 判别法.张起帆注意到,在有限域上Hermite 判别法恰好可以看作Newton 公式的补充.在Williams 的证明中使用Hermite 判别法取代Newton 公式,就可以规避小特征障碍,从而改进了Williams[12]的结果,并得到了一个完全线性代数化的初等证明.事实上,他得到了
定理1.7(Zhang) 有限域Fq上多项式f(X)是置换多项式,当且仅当存在正整数m,使得
1)f 满足前2m-1 个Hermite 条件.
定理1.8 有限域Fq上多项式f(X)是置换多项式,当且仅当存在正整数m,使得
1)f 满足前m-1 个Hermite 条件.
2)f 在Fq中有(q-m)个单簇点.
其中,称a ∈Fq为f 的一个单簇点,若f(X) =a 在Fq中有唯一解.
推论1.9 有限域Fq上多项式f(X)是置换多项式,如果存在正整数m,使得
等价地,我们有
等价描述设有限域Fq上次数为d 的多项式f(X)不是置换多项式,若存在正整数m,使得f 满足前2m-1 个Hermite 条件,那么f 的值集大小.特别地,
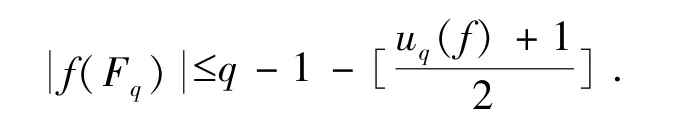
其中uq(f)为f 满足前k 个Hermite 条件的最大的k ≤q-2,而且万大庆与张起帆的结果均可导出Cohen 定理1.3.
2 一些预备工作
首先介绍一下所要用到的有限生成代数相关知识(详细参见文献[13-14]).令K 为一个域,称A 为域K 上(有限生成)n 维代数,若A 既是域K 上n 维向量空间,本身又是环,且满足
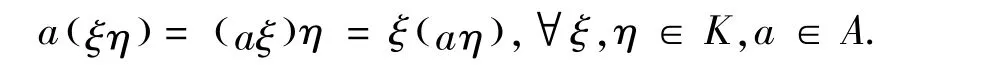
对∀ξ ∈A,存在自然的线性变换Tξ:

自然对线性变换Tξ,可以定义(线性代数的)迹Tr(Tξ),从而也可以定义A 中元素ξ 对于A/K 的迹为Tr(Tξ);进一步地,设线性变换Tξ在取定的某组基(ξ1,…,ξn)下有变换矩阵M(ξ),对应特征值为λ1,…,λn,则ξ 对于A/K 的迹还可写作:

特别地,令K=Fq,设Fq[x]为Fq上全体函数的集合,则易验证知Fq[x]构成域Fq上的q 维代数,且有同构成立:

对于Fq[x]中函数f:x |→f(x),直接记为f(x)或f;特别地,Fq上恒等函数I dFq记作x.

利用上述的结果,我们也可重述Hermite 判别法为:
定理2.1 (Hermite 判别法,迹形式)
同理,令S 为有限域Fq上一个给定的n 元子集.设AS为S 到Fq上的所有函数全体构成的集合,则AS也构成Fq上(有限生成)的n 维代数,且有自然的同构:
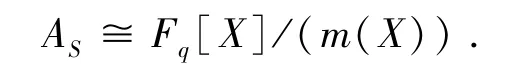
之后讨论中,若无特别注明,均将AS中函数f 对于AS/Fq的迹略写为Tr(f).
3 主要定理与推论
定理3.1 对S 到Fq上函数f(x),有
这里右侧等式中x 指S 上的恒等函数
证明 必要性显然,只需证明充分性.事实上,令g ∈Fq[X]为满足下列条件的多项式函数:

那么在此定义下,g(x)至少有(q-n)-n=q-2n 个单簇点,且有

由定理1.8,g 必然是Fq上的置换多项式,从而f 必然是S 到S 上的双射.
如果S=Fq,那么定理3.1 自然导出Fq上经典形式的Hermite 判别法,因而定理3.1 确为Hermite 判别法在子集上的推广.
进一步地,利用类似方法,有
定理3.2 对S 到Fq上函数f(x),f(x)是S 上双射当且仅当存在正整数m,使得
1)Tr(fk) =Tr(xk),k=0,1,…,2m-1.
特别地,限制f 为S 到S 上函数,则f(x)是S 上双射当且仅当存在正整数m,使得
1)Tr(fk) =Tr(xk),k=0,1,…,2m-1.
证明同定理3.1 一样构造多项式函数g(x),迹等式条件自然成立;只需再注意到
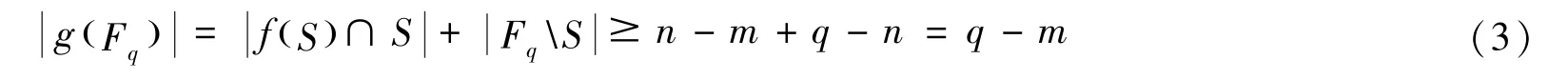
由定理1.7 即知g 必然是Fq上的置换多项式,从而f 必然是S 到S 上的双射.
现在考虑次数推论的推广;考虑f 的Lagrange 插值多项式f0(X),我们有
推论3.3 对S 到Fq上函数f(x),f(x)是S 上双射,如果存在正整数满足
其中Uf是使得Tr(xk) =0,1 ≤i ≤k 成立的最大的k ≤n-2.
特别地,限制f 为S 到S 上函数,则f(x)是S 上双射,如果存在正整数m,使得
其中Uf是使得Tr(xk) =0,1 ≤i ≤k 成立的最大的k ≤n-2.
证明注意到有自然的多项式表示,从而可由x 的不超过kdeg f0次幂的迹线性表出,而所给条件表明对0 ≤k ≤2m-1,这些迹均为0,从而Tr(fk)和Tr(xk)均为0,满足迹等式条件,从而由定理3.2 得证.
最后,同置换多项式的情况类似,如果S 到Fq上函数f 在S 上不满,且f 满足前一些迹等式条件,那么f(S)不能包含太多S 中的元素(否则依前述,f 为双射,矛盾).由此,我们可以将Fq中多项式上界估计推广到子集上.事实上,我们有
推论3.4 假设函数f:S →Fq,f(S)S.如果存在正整数m 使得Tr(fk-xk)=0,k=0,1,…,2m-1,那么f(S)不能包含多于n-1-m 个S 中的元素.特别地,

若限制f 为S 到S 上函数,则函数f 值集大小有上界估计

其中u(f)是使得Tr(fk-xk) =0,1 ≤i ≤k 成立的最大的k ≤n-2.
4 .特殊子集上的讨论
μn上所有函数的集合Aμn显然构成Fq上有限生成n 维代数,进一步有自然的同构:
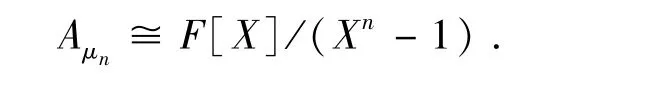
对子集μn,有
定理4.1

证明 对S=μn,应用定理3.1,有f(x)为μn到μn上的双射Tr(fk) =Tr(xk),k=0,1,…,2n-1
注意到n 次单位根群μn是循环群,即μn=(ξ0),其中ξ0为n 次本原单位根,从而只需验证前n 个迹等式条件成立.时,,从而

而k=0 时Tr(xk)=Tr(fk)=Tr(1)=n 自然成立,从而第一个等价条件成立.又对插值多项式f0(X)=,有

即知第二个等价条件成立.
进一步地,我们有推论
推论4.2 对μn到μn上函数f(x),f(x)是μn上双射当且仅当存在正整数m,使得
1)Tr(fk) =0,k=1,…,2m-1.
等价地,我们有
等价描述假设函数f:μn→μn不是双射,如果存在正整数m 使得Tr(fk) =0,k=1,…,2m-1,那么f(μn)取值个数不能多于n-1-m.特别地,函数f 值集大小有上界估计
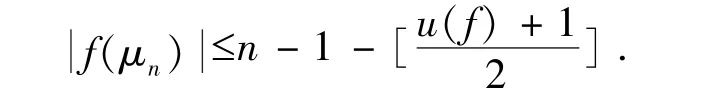
其中u(f)是使得Tr(fk) =0,1 ≤i ≤k 成立的最大的k ≤n-2.
最后,若插值多项式f0无常数项且次数足够小,那么可以导出与万大庆类似的结果:
推论4.3 对μn到μn上函数f(x),f(x)是μn上双射,如果存在正整数m,使得
1)f0( 0)=0,
其中f0(X)是f 在μn[x]上的Lagrange 插值多项式.
等价地,我们有
等价描述假设函数f:μn→μn不是双射,d=deg(f0)为Lagrange 插值多项式f0(X)的次数,若f0(0) =0,那么对任意满足的正整数m,f(μn)取值个数不能多于n-1-m.特别地,函数f 值集大小有上界估计

5 结论
通过导入有限生成代数观点,将有限域上Hermite 判别法成功推广到了其子集上,并在子集上推广了有限域上的函数相关的多个重要结果,并给出了计算实例;为有限域相关的理论在一般子集上的推广提供了一个新思路,主要结果对于有限域上特定子集的函数及自同态相关研究也有一定意义.

