变时滞非线性中立型微分方程的稳定性

黄明辉，赵国瑞

(广州城建职业学院，广东 广州 510925)

1 预备知识

时滞非线性微分方程的研究，长期以来一直受到广大研究者的关注[1-12]. Jin、Zhang 等学者利用不动点理论研究了微分方程的稳定性，并取得了一系列的研究成果[13-16].2011 年，文献[1]利用不动点理论，研究了时滞线性中立型微分方程

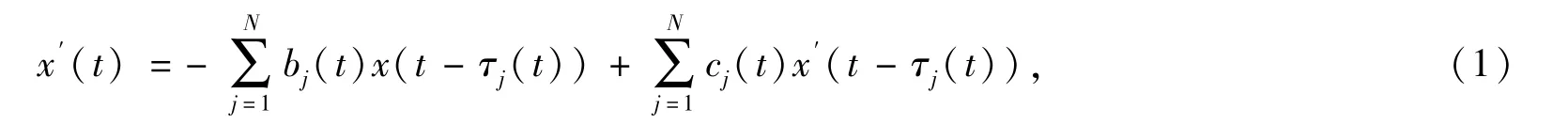
零解的渐近稳定性.2012 年，文献[2]利用不动点理论，研究了时滞线性中立型积分微分方程

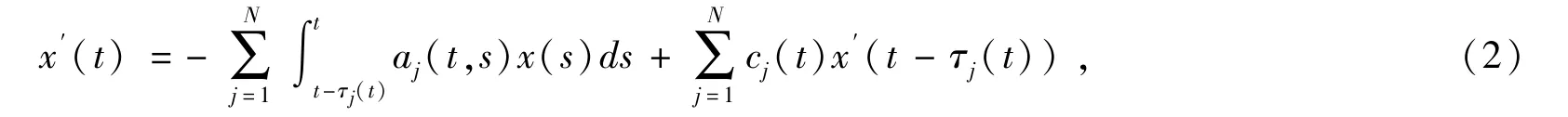
零解的渐近稳定性.然而，上述结果的条件非常严格，要求c 可微且τ 二次可微，τ′(t)1，t ∈[0，∞).受此启发，本文考虑以下变时滞非线性中立微分方程零解的渐近稳定性

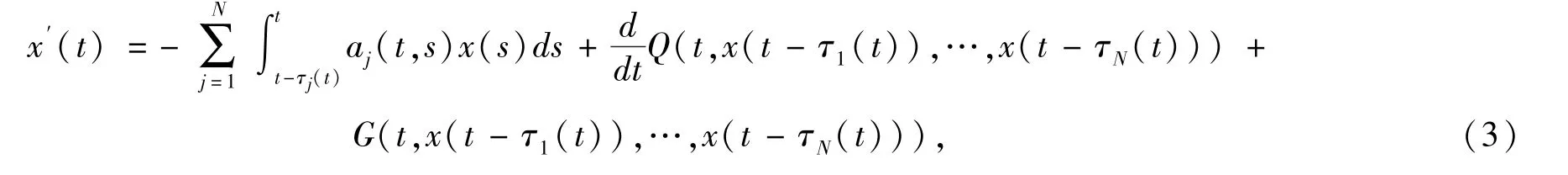
及初始条件x(t) =ψ(t)∈C([m(t0)，t0]，R)，对任意t0≥0，有mj(t0) =inf{t-τj(t)，t0≥0}，m(t0) =min{mj(t0)，1 ≤j ≤N}.

2 主要结果

定义1 对任意(t0，φ)∈[0，∞)×C([m(t0)，t0]，R)，若x ∈C([m(t0)，∞))在[t0，∞)上满足方程(3)，且当t ∈[m(t0)，t0]时，x(t) =φ(t)，则称x 为方程(3)经过(t0，φ)的解，记为x(t) =x(t，t0，φ).

引理1 方程(3)等价于

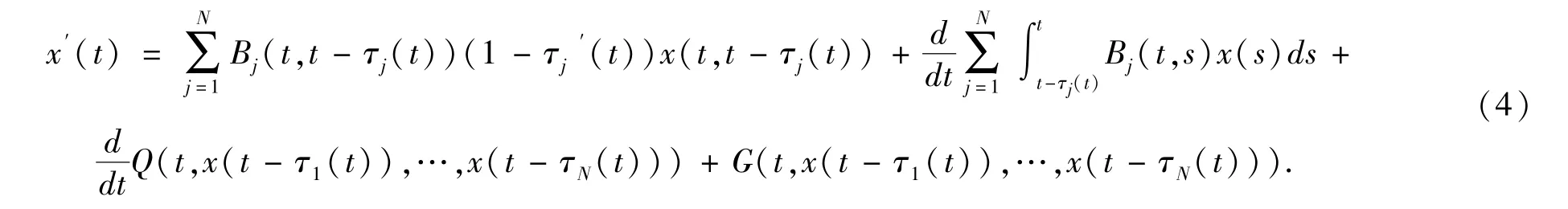
对方程(3)给出下列假设:

(H1)aj∈C(R+×[m(t0)，∞]，R)，τj∈C(R+，R+)且可微，当t →∞，t-τj(t)→∞，其中j=1，2，…，N.

(H2)Q(t，x1，…，xN)，G(t，x1，…，xN)对x1，…，xN是全局Lipschitz 连续函数，即存在正数L1，…，LN和K1，…，KN，

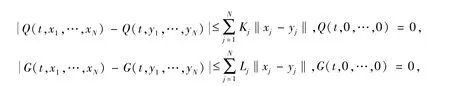
(H3)存在连续函数hj:[m(t0)，∞]→R，j=1，2，…，N 和常数α ∈(0，1)，对t ≥0，

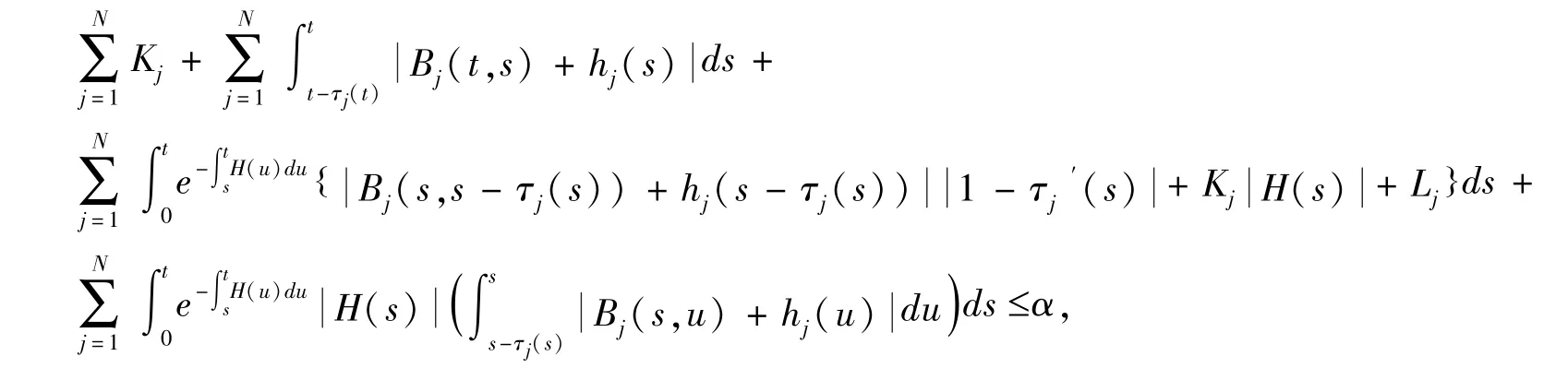
定理1 设(H1)-(H3)成立.若，则方程(3)的零解渐近稳定.

证明对任意t0≥0，设.对固定的ψ ∈C([m(t0)，t0]，R)，令Sψ= { x ∈ C([m(t0)，∞]，R):t →∞，x(t)→0 且x(t) =ψ(t)，t ∈[m(t0)，t0]}，

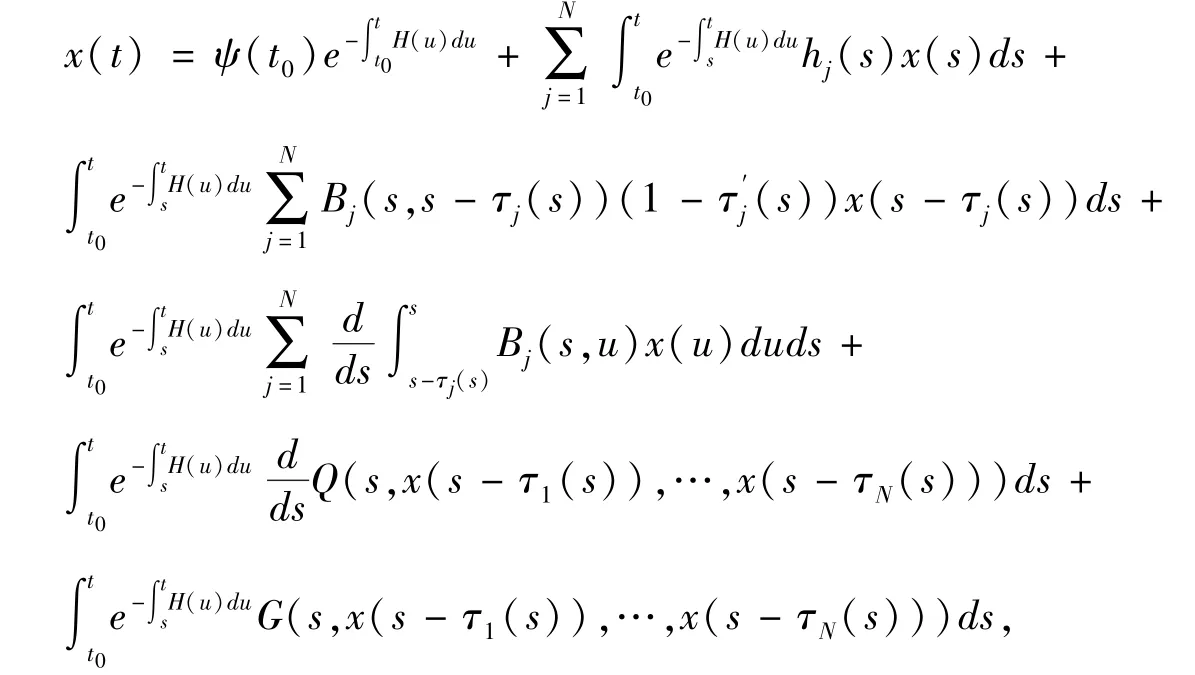
通过分部积分并整理，得

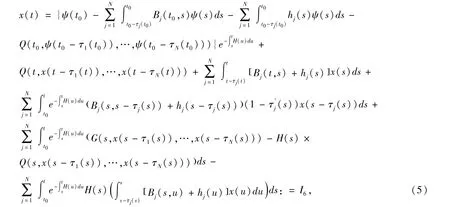
定义映射P:Sψ→Sψ:对任意t ∈[m(t0)，t0]，(Pφ)(t) =ψ(t)，当t ≥t0，

显然，(Pφ)∈C([m(t0)，∞]，R).现在证明当t →∞时，(Pφ)(t)→0.由于t →∞时，φ(t)→0 和t-τj(t)→∞.因此，对任意ε ＞0，存在T1＞t0，使得当s ≥T1，有.因此，当t ≥T1，(6)中的最后一项I6满足

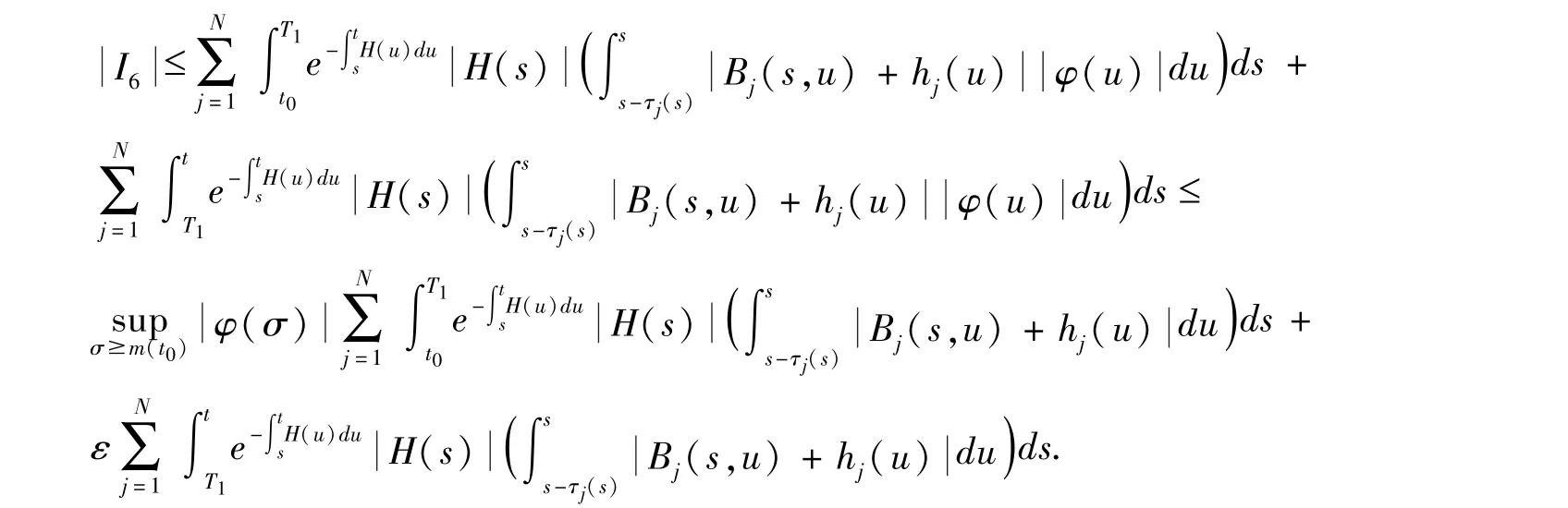
此外，存在T2≥T1，使得当t ≥T2，

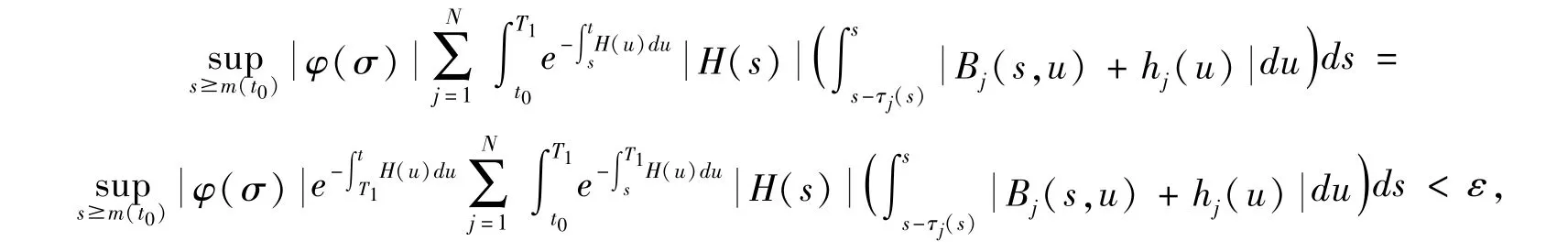
设任意φ，ψ ∈Sψ，当t ≥t0时，

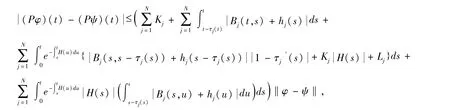
由条件(H3)可得，P 是一个压缩系数为α 的压缩映射.所以，由压缩映射原理得，P 在空间Sψ上存在唯一不动点x(t)，它是方程(3)的解.且x(t)满足当t ∈[m(t0)，t0]，x(t)=ψ(t)，当t →∞时，x(t，t0，ψ)→0.

为了证明渐近稳定性，需要证明方程(3)的零解是稳定的. 假设给定任意ε ＞0 和δ ＞0(ε ＜δ)满足.如果x(t) =x(t，t0，ψ)是方程(3)的一个解，其中‖ψ‖＜δ，对任意t ≥t0，x(t) =(Px)(t).下面证明t ≥t0，

显然，当s ∈[m(t0)，t0]，有.如果存在t∗＞t0，使得x(t∗) =ε，且当m(t0)≤s ＜t∗，有，则由(6)得

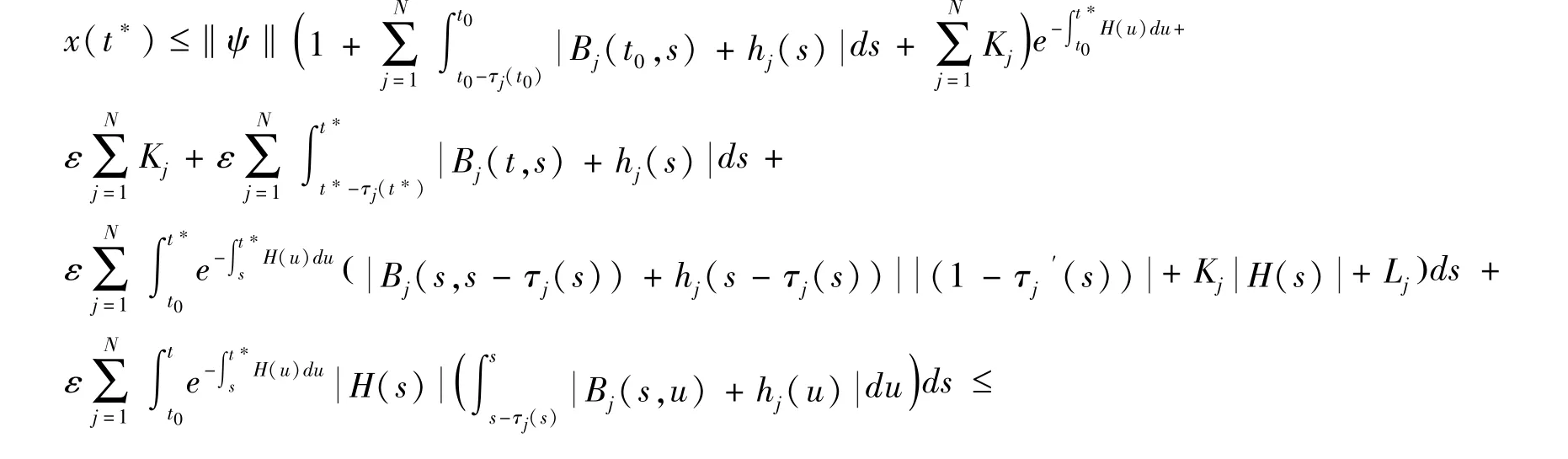
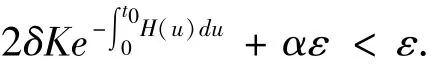
这与t∗的定义相矛盾.这说明，如果成立，方程(3)的零解渐近稳定.

3 应用举例

例1 考虑以下变时滞非线性中立微分方程

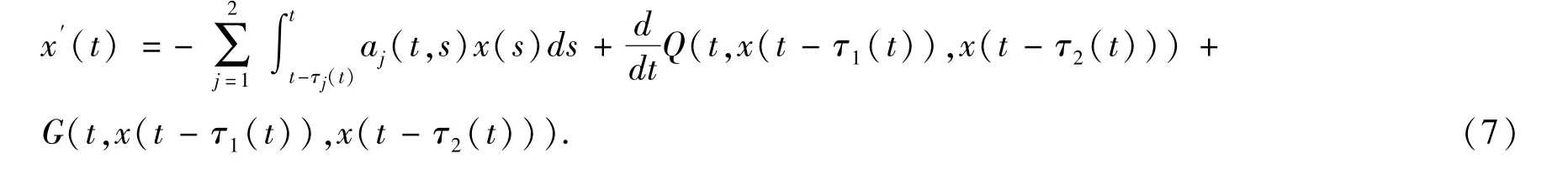
其中τ1(t) =0.489t，τ2(t) =0.478t，a1(t，s) =0.48/(s2+1)，a2(t，s) =0.52/(s2+1)，

Q(t，x，y) =0.072sin ( x/2)+0.036sin ( y/3)，G(t，x，y) =0.

证明选取h1(t) =0.52t/(t2+1)，h2(t) =0.48t/(t2+1)，则H(t) =t/(t2+1)，

通过简单的计算可得，K1=0.036，K2=0.012，L1=L2=0，

因此，α=0.048+0.386+0.386+0.1125=0.9325 ＜1，定理1 中的所有条件成立.由定理1 可得方程(7)零解是渐近稳定的.

4 结论

本文利用不动点理论，研究变时滞非线性中立型微分方程零解的渐近稳定性. 所研究的方程引入了和G(t，x(t-τ1(t))，…，x(t-τN(t)))，比文献[1-2]中的方程更加一般化.并且文献[1-2]的定理要求时滞τ 二次可微，τ′(t)1，t ∈[0，∞)，但本文定理1 中仅要求τ 连续可微，进一步削弱了对时滞τ 的要求，从而推广了文献[1-2]的相应结果.