上埋式涵洞基础埋深效应下的地基承载力研究

冯忠居1，李少杰2，郝宇萌1，董芸秀1，方元伟1，胡海波1，潘 放，李 军

(1.长安大学 公路学院，西安 710064；2.中铁建设集团有限公司，北京 100040； 3.广东包茂高速公路有限公司，广州 510000)

1 研究背景

高速公路工程中很多涵洞未考虑基础埋深效应对地基承载力的影响，使涵洞地基承载力设计值偏高，地基刚度过大，导致涵洞出现不同程度的病害[1-5]。涵洞结构受力情况与一般构筑物有很大区别，导致在计算地基承载力时有所不同。高填方涵洞涵顶存在垂直土压力集中现象[6-10]，它对涵侧地基所受土压力有很大影响。因此在确定涵洞地基承载力时，应根据涵顶应力集中现象[11-16]确定基础埋深对地基承载力的影响。

在确定地基承载力的研究手段方面， 主要方法包括现场荷载试验法、 理论公式计算法和数值计算法3类。 现场试验法不能得到考虑基础埋深效应的地基承载力， 而理论公式和数值计算法可以考虑基础埋深效应和参数变化的影响； 此外， 数值计算法能得到涵顶和基底土压力的分布情况。 在地基承载力的研究成果方面， 20世纪20年代， 普朗特尔提出地基极限承载力计算公式[17]， 但该公式没有考虑基础埋深效应对地基承载力的影响， 其计算值明显低于涵洞地基承载力。 20世纪40年代， 太沙基考虑了基础埋深效应的影响， 使计算得到的地基承载力有所提高[17]， 但该公式不符合涵洞地基实际受力情况。 文献[18]—文献[20]通过室内模型试验将涵侧填土作为堆载探讨埋深效应的影响， 在试验过程中涵洞与周围填土没有接触， 不符合涵洞的真实受力情况。 文献[21]—文献[22]通过有限元软件研究埋深范围内的土体强度对地基承载力的影响， 但该成果亦不适用于涵洞地基承载力计算。 文献[23]利用数值方法计算构造物地基的极限荷载， 并与太沙基公式和斯凯普顿公式的计算结果进行比较， 但并没有对涵洞地基受力情况进行探讨。 《公路桥涵地基与基础设计规范》(JTG D63—2007)[24]指出当埋置深度>3 m时， 对桥涵地基承载力进行深度修正， 但这种计算方法偏向于经验取值， 没有进行理论验证。 上述研究虽在涵洞地基承载力方面取得了一定的进展， 但由于涵洞结构的应力集中现象， 使得一般的地基承载计算方法对涵洞不完全适用。 因此， 有必要对涵洞基础埋深效应下的地基承载力展开研究。

本文基于太沙基理论与顾安全公式，分析基础埋深效应对上埋式涵洞地基承载力的影响，并推导涵洞地基承载力公式。利用有限元软件Midas-GTS，由地基土荷载-沉降(P-S)曲线确定不同填高下的地基承载力容许值，并将本文成果与前人成果进行对比，同时分析了不同填土高度下涵顶和基底土压力变化规律。最后，分析了不同计算方法下地基土的抗剪强度对地基承载力的影响。以期为确定上埋式涵洞地基承载力提供理论支撑。

2 太沙基地基承载力理论

2.1 太沙基理论基本假定

(1)基础底部是粗糙的。如图1所示，由于基底以下存在摩擦力，阻止了基底下Ⅰ区土楔体ABC的剪切破坏，这部分土体不发生破坏而处于弹性状态，它就像一个“弹性核”随着基础一起向下移动。

图1 太沙基公式滑动面形状Fig.1 Shape of sliding surface by Terzaghi’s formula

(2)地基土是有质量的(重度γ≠0)，但忽略地基土重度对滑移线形状的影响。因为根据平衡理论，如果考虑土的重度，塑性区内的2组滑移线就不一定全是直线，太沙基的滑动面形状如图1所示。

(3)基底以上的土体看作是作用在基础两侧的均布荷载q=γd，其中d为基础埋置深度，考虑基础的埋深效应。

2.2 太沙基地基承载力公式

基于上述假定，若作用在基底的极限荷载为Pu，假设此时基底土体发生剪切破坏，可得地基承载力公式为

(1)

式中：Nr，Nq，Nc为地基承载力系数，仅与土的内摩擦角φ有关；b为基础宽度；c为地基土黏聚力。

3 上埋式涵洞地基承载力公式

3.1 上埋式涵洞地基承载力埋深效应

太沙基地基承载力公式中的基础埋深效应没有涉及上埋式涵洞的受力情况，其与涵洞地基承载力实际情况存在较大差异。由于涵洞与填土的刚度差异，涵顶内填土的沉降往往小于外填土，涵顶外填土的部分自重通过剪切力传递至内填土，导致涵顶产生应力集中现象，台背填土受到向上的附加土压力Δσv。20世纪60年代初，顾安全教授[25]根据室内模型试验结果，提出了用管顶沉降差δ来概括土压力的各种影响因素，并提出了土压力的计算公式。涵洞台背填土所受土压力为

(2)

式中：H为涵顶以上填土高度(m)；h为涵洞凸出地面高度(m)；D为涵洞宽度(m)；ωc为与涵洞的长宽比(L/D)有关的系数；μ为涵顶填土的侧膨胀系数(泊松比)；E，Eh分别为涵顶以上高度H及涵洞两侧同高度h的填土变形模量平均值(kPa)。

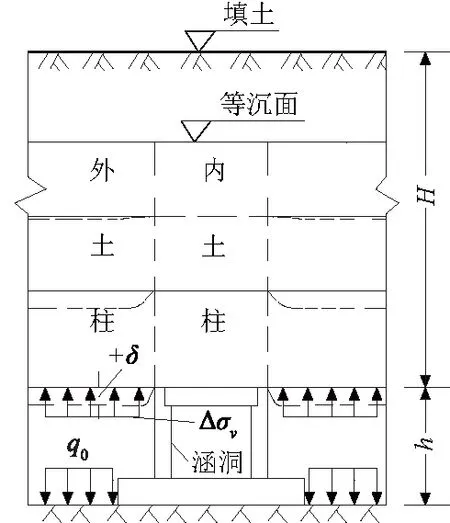
图2 上埋式涵洞地基受力 示意图Fig.2 Forces acting on the buried culvert foundation

基于太沙基理论与顾安全公式，本文提出假设：涵洞台背光滑，即涵洞台背与填土之间无摩擦力。如图2所示，涵顶外填土受到向上的附加压力Δσv(与顾安全公式中的确定方法一致)。因此涵侧地基所受土压力q0为上覆填土自重γ(H+h)减去涵顶台背填土附加土压力Δσv，即

q0=γ(H+h)-Δσv=

(3)

综上所述，在计算上埋式涵洞地基承载力时，涵洞基础的埋深效应要考虑涵侧土体自重γH和涵顶外填土附加压力Δσv的综合影响。

3.2 上埋式涵洞地基承载力公式推导

如图3所示，Ⅰ区为弹性压密区，它与基础底面一起移动。滑动面AC(或BC)与水平面成φ角。Ⅱ区为过渡区，滑动面一组是辐射线，另一组是对数螺旋曲线CD和CE，其方程式为r=r0eθtanφ。Ⅲ区是朗金被动状态区，滑动面AD及DF与水平面成(π/4-φ/2)角。q0为涵侧填土产生的土压力，其计算方法如式(3)所示，基础的埋深效应将使地基承载力提高。

图3 本文公式滑动面形状Fig.3 Shape of sliding surface by the formula proposed in this paper

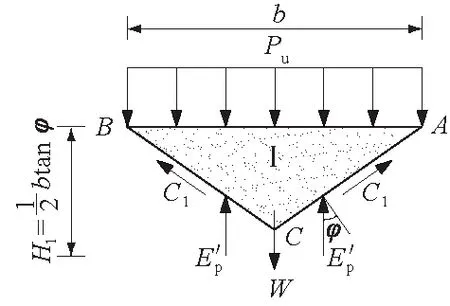
图4 土楔体ABC受力 示意图Fig.4 Forces acting on soil wedge ABC

若作用在基底的极限荷载为Pu，假设此时发生整体剪切破坏，那么基底下的弹性压密区(Ⅰ区)ABC将贯入土中，向两侧挤压土体ACDF及BCEG达到被动破坏。如图4所示，取脱离体ABC，考虑单位长基础，根据平衡条件，有

Pub=2c1sinφ+2Ep-W。

(4)

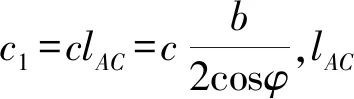
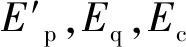
(5)

Ec=cH1Kpc;

(6)

Eq=q0H1Kpq。

(7)

式中：Kpγ，Kpc，Kpq分别为由土重γ、黏聚力c、荷载q0产生的被动土压力系数(无量纲)。

将式(3)、式(5)、式(6)、式(7)代入式(4)可得地基承载力公式，即

c[tanφ(1+Kpc)]。

(8)

将地基承载力公式(8)简化，可得

(9)

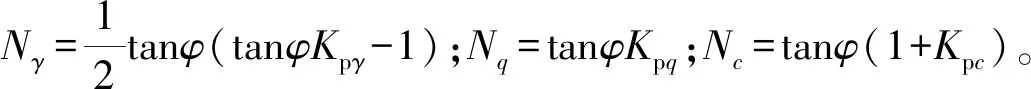
本公式中涵顶填土高度H>0，否则附加土压力Δσv对地基承载力没有影响。

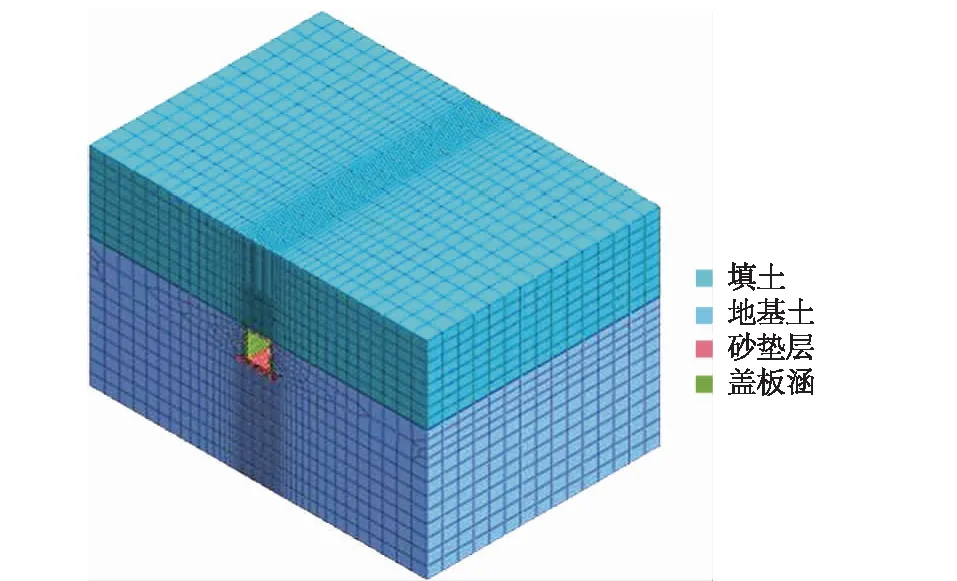
图5 模型网格划分Fig.5 Meshing of the model

4 数值模拟与成果分析

4.1 模型的建立与参数的选取

有限元法具有较强的后处理功能和先进的非线性分析功能，能真实地反映地基破坏机理和破坏过程[21]。Midas-GTS是专门用于岩土工程分析的有限元软件，本文用它来分析上埋式涵洞基础的埋深效应对地基承载力的影响。为保证填土荷载作用下涵洞体的承载能力，涵洞采用钢筋混凝土结构，以满足涵洞的强度和正常使用的要求。由于Mohr-Coulomb屈服准则可以很好地描述大多数土体由弹性状态向塑性状态的演变过程[21]，弹性模型能较好地反映混凝土、钢筋的特性，因此本文选择Mohr-Coulomb屈服准则作为土体的本构模型进行模拟，混凝土和钢筋选择弹性模型进行模拟，其中钢筋采用一维桁架单元模拟，其他采用三维实体单元模拟。模型两侧仅约束水平位移，模型底部同时约束水平和竖向位移。如图5所示，模型水平方向长度为120 m，宽度为60 m。其中涵洞类型为盖板涵，涵洞净高度为6.2 m，净宽度为5.4 m，顶板和侧墙厚度均为0.8 m；基础尺寸为60 m×10 m×1.5 m。顶板下缘和底板上缘受力筋分别采用36B28mm和15B20mm。本文分别设置填土高度为8.5，13.5，18.5，23.5，28.5 m(以涵洞基础底面为基准)，涵洞台背高度为8.5 m。模型参数选取如表1所示。

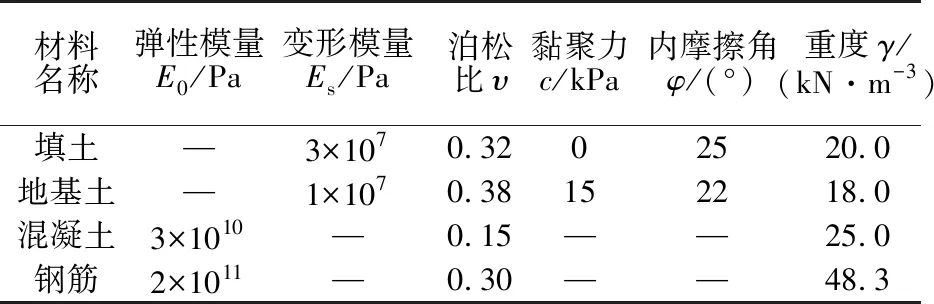
表1 模型参数Table 1 Model parameters

4.2 分析工况

为全程模拟地基从初始线弹性状态逐渐过渡到塑性流动的极限状态的破坏过程，本文针对不同工况在涵洞基础上分级加载，即采用施工阶段求解类型先进行模型在自重条件下初始状态的计算，然后位移清零，对涵洞基础分级加载(共加10级荷载)，最后根据不同工况下地基土体的荷载-沉降(P-S)曲线，确定地基承载力的大小。具体分析工况如表2、表3所示。

表2 填土高度分析工况Table 2 Working conditions of analyzing soil fill height

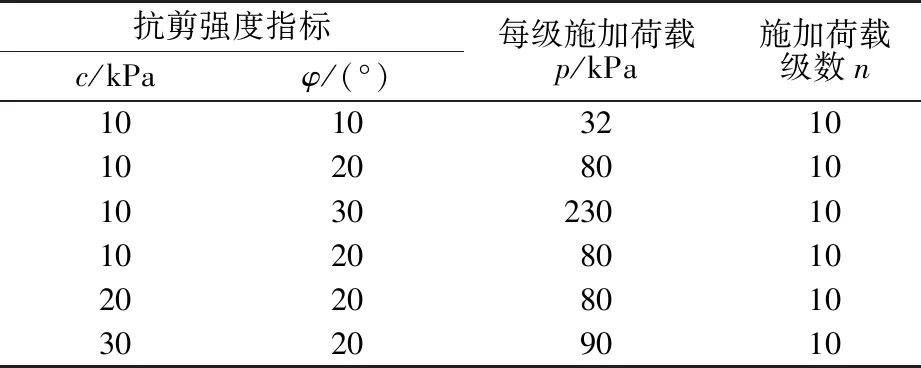
表3 地基土体抗剪强度分析工况Table 3 Working conditions of analyzing shear strength of foundation soil

4.3 数值模拟与理论成果分析

4.3.1 不同填土高度对地基承载力的影响分析

根据《公路桥涵地基与基础设计规范》(JTG D63—2007)附录D.0.6与《建筑地基基础设计规范》(GB 50007—2002)附录C.0.6的要求，取第2特征屈服点确定地基承载力容许值[24-26]。不同相对填土高度下地基土的荷载-沉降(P-S)曲线如图6所示，地基承载力容许值及其提高率如表4所示。

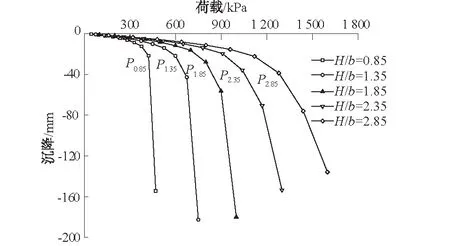
图6 不同相对填土高度的荷载-沉降(P-S)曲线Fig.6 Load-settlement (P-S) curves in the presence of varied relative soil fill heigh

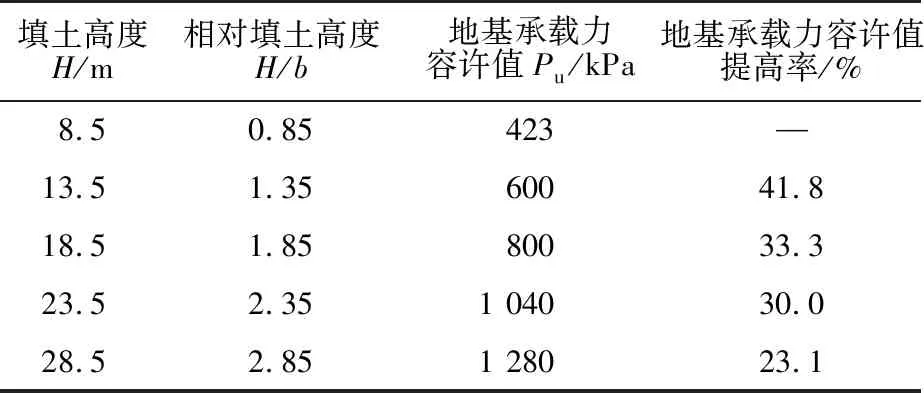
填土高度H/m相对填土高度H/b地基承载力容许值Pu/kPa地基承载力容许值提高率/%8.50.85423—13.51.3560041.818.51.8580033.323.52.351 04030.028.52.851 28023.1

表5 不同方法计算的地基承载力容许值及误差Table 5 Allowable values and errors of bearing capacity of foundation calculated by different methods

如图6所示，P0.85，P1.35，P1.85，P2.35，P2.85分别表示相对填土高度H/b为0.85，1.35，1.85，2.35，2.85时的地基承载力容许值。随着荷载的增加，地基土沉降呈非线性增大，当荷载达到地基承载力容许值之后，地基土沉降急剧增大，土体发生剪切破坏。如表4所示，随着相对填土高度的增加，地基承载力容许值不断增大，说明涵侧填土作为旁压荷载限制土体发生剪切破坏，增强了地基土的抗剪强度，使涵洞地基承载力得到提高。当相对填土高度为1.35，185，2.35，2.85时，地基承载力容许值的提高率分别为41.8%，33.3%，30.0%，23.1%(以上一级相对填土高度H/b的地基承载力容许值为基准)，地基承载力的提高率逐渐降低，说明填土高度增加在一定程度上限制了地基土的运动，并且其限制程度趋于稳定。

不同计算方法下的地基承载力对比曲线如图7所示，不同计算方法的地基承载力容许值及误差如表5所示。

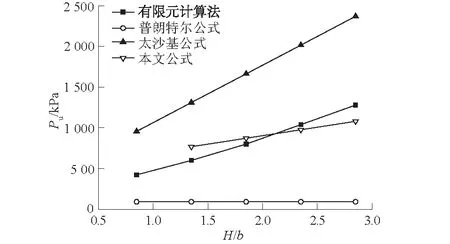
图7 不同计算方法下地基承载力容许值对比曲线Fig.7 Comparison of allowable value of bearing capacity of foundation among different calculation methods

由图7可以看出，由于普朗特尔计算公式没有考虑基础的埋深效应，地基承载力计算值为恒定值，且明显低于其他计算方法，与有限元计算值差异较大，显然不符合实际情况。其余3种计算方法的地基承载力容许值随填土高度的增加逐渐增大，基础的埋深效应增强了地基承载力。太沙基公式没有考虑涵顶的应力集中现象，涵侧填土自重完全等同于旁压荷载，使计算值远远大于有限元计算值，误差较大。本文推导的地基承载力公式充分考虑涵顶应力集中现象引起涵洞台背填土产生向上的附加土压力，更能反映地基所受土压力的真实情况，计算值与有限元结果误差较小，更加适用于涵洞地基承载力计算。如表5所示，相对填土高度在0.85～2.85的变化过程中，普朗特尔公式的误差依次为-78.49%，-84.83%，-88.63%，-91.25%，-92.89%，太沙基公式的误差依次为126.24%，118.33%，107.88%，93.85%，85.08%，本文地基承载力公式的误差依次为28.00%，9.00%，-6.15%，-15.63%，本文公式与有限元法最为吻合。

4.3.2 不同填土高度下的涵顶和基底土压力分析

不同填土高度下涵顶和基底垂直土压力分布曲线如图8所示。

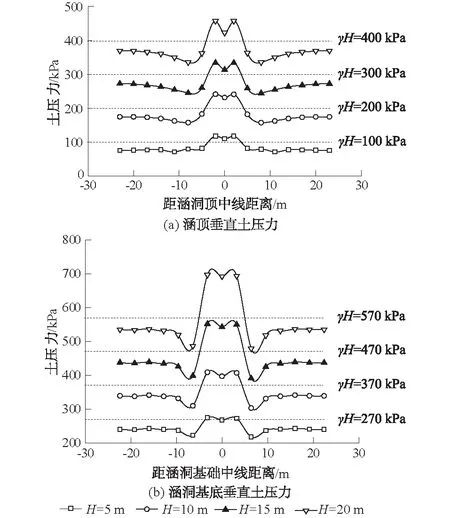
图8 不同填土高度下涵顶、涵洞基底垂直土压力分布曲线Fig.8 Curves of vertical soil pressure on top of culvert and at the base of culvert in the presence of varied soil fill height

如图8(a)所示，涵顶垂直土压力随距涵顶中线距离的变化呈“马鞍形”分布，即涵顶垂直土压力较大，台背填土土压力较小。在不同填土高度下，涵顶垂直土压力大于上覆土自重γH，涵洞台背填土土压力均小于上覆土自重γH，说明涵顶发生应力集中现象，台背填土受到向上的附加土压力。随着距涵顶中线距离的增加，涵顶垂直土压力先减小后增大。随着填土高度的增加，涵顶垂直土压力曲线“凸起”程度越大，涵顶内、外土压力差值增加，涵洞台背填土受到附加土压力的影响越大，说明涵洞在高填方的条件下，本文所考虑的基础埋深效应受附加土压力影响较大。如图8(b)所示，涵洞基底垂直土压力随距基底中线距离的增加呈“马鞍型”分布。在距基底中线距离的变化过程中，基底土压力分布规律与涵顶土压力相似。由于涵顶应力集中的影响，基底外填土所受土压力均小于上覆土自重γH，充分说明在地基承载力计算中不应以上覆填土自重作为旁压荷载，本文公式更符合实际情况。

4.3.3 不同土体抗剪强度对地基承载力的影响分析

以填土高度H=18.5 m为例，在不同地基土的抗剪强度下，由不同计算方法得出的地基承载力容许值对比曲线如图9所示，不同方法计算的地基承载力容许值及误差如表6、表7所示。

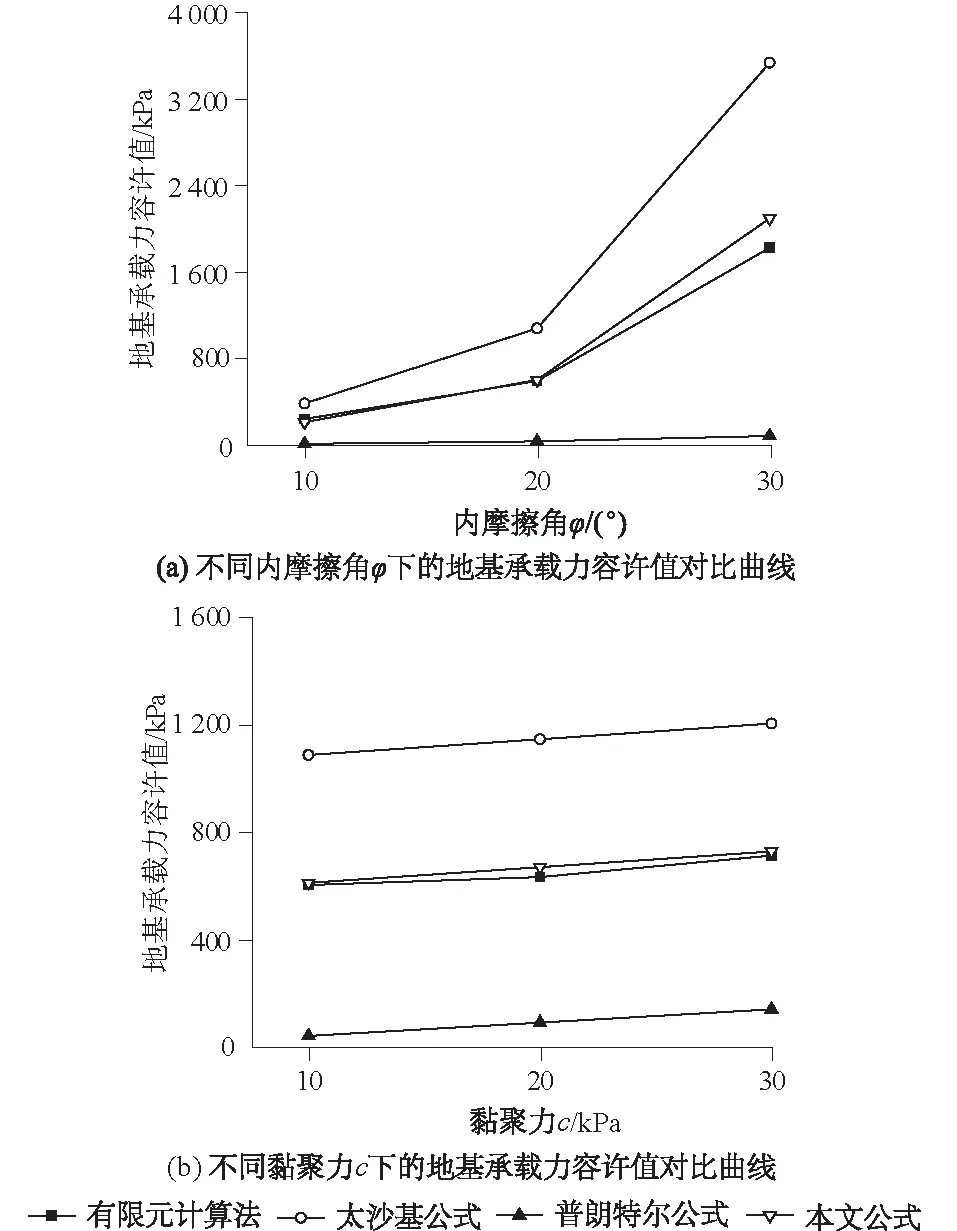
图9 不同抗剪强度指标下的地基承载力容许值 对比曲线Fig.9 Comparison of allowable value of foundation’s bearing capacity under different shear strength indices among different calculation methods

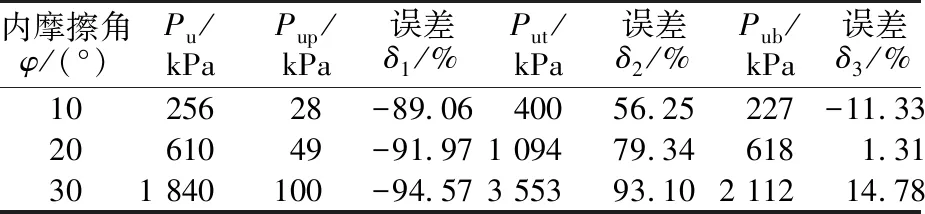
内摩擦角φ/(°)Pu/kPaPup/kPa误差δ1/%Put/kPa误差δ2/%Pub/kPa误差δ3/%1025628-89.0640056.25227-11.332061049-91.971 09479.346181.31301 840100-94.573 55393.102 11214.78

表7 不同方法计算的地基承载力容许值及误差 (φ=20°)Table 7 Allowable values and errors of bearing capacity of foundation calculated by different methods when φ=20°

如图9(a)所示，随着地基土的内摩擦角φ的增大，地基承载力容许值非线性增长。由于普朗特尔计算法没有考虑基础的埋深效应，其增长幅度很小。相反，其余计算方法得出的地基承载力容许值的增长幅度较大。如表6所示，普朗特尔与太沙基计算公式得出的地基承载力容许值与有限元计算值误差较大，其最大误差分别为-94.57%和93.10%；本文公式计算得出的地基承载力容许值与有限元计算值误差较小，地基土的内摩擦角φ分别为10°，20°，30°时，地基承载力容许值的误差分别为-11.33%，1.31%，14.78%。如图9(b)所示，随着地基土黏聚力c的增加，地基承载力容许值近似呈线性增长趋势，但其增长幅度较小，说明内摩擦角φ对地基承载力的影响程度明显大于黏聚力c。如表7所示，本文公式与有限元法的计算值最为吻合，误差最小，地基土的黏聚力c为10，20，30 kPa时，地基承载力容许值的误差分别为1.31%，5.78%，2.08%。此外，当地基土强度较大，即抗剪强度指标较高(φ=30°)时，理论计算值与有限元法的计算值的误差较大(相对于抗剪强度指标较低的情况)，这是因为在地基强度较高时，地基土不易发生整体剪切破坏，按照强度理论法计算得出的地基承载力值偏高。

5 工程实例与现场测试

5.1 现场条件及测点布置

本文选取包茂高速(粤境段)K13+198.5(4×4盖板涵)为土压力监测涵洞，涵长87.8 m，盖板厚度为0.8 m，侧墙中部、底部厚度分别为0.7 m和1.05 m，底板厚度为1.5 m。现场涵洞地基换填土参数如表8所示。选取具有代表性的2个断面作为监测断面，如图10(a)，其中Ⅰ断面在路基中心线处，Ⅱ断面在路肩内侧70 cm处。在Ⅰ断面、Ⅱ断面涵洞基底埋设5个振弦式土压力盒观测涵洞基底土压力随填土施工过程中的变化规律,如图10(b)。

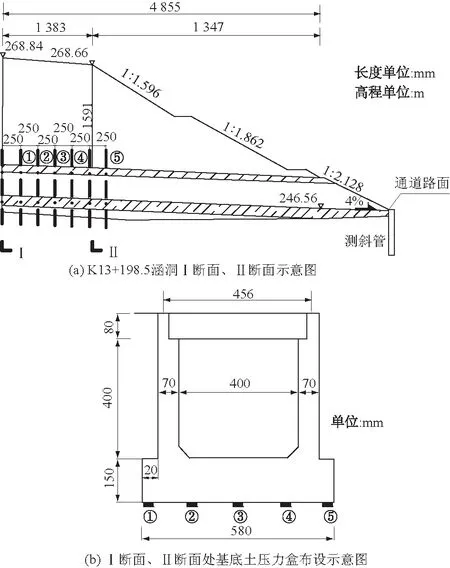
图10 断面示意图及基底土压力盒布设Fig.10 Schematic diagram of sections and layout of earth pressure gauges

材料名称变形模量Es/Pa泊松比υ黏聚力c/kPa内摩擦角φ/(°)重度γ/(kN·m-3)砂砾土5×1070.2503222.0

5.2 不同填土高度下基底土压力与地基承载力对比分析

K13+198.5涵洞现场设计要求地基承载力达到620 kPa，该涵洞地质勘察资料表明，涵洞基底以下4～5 m范围以内为粉质黏土，地基承载力约为200～250 kPa，天然地基承载力无法满足设计要求。因此，采用砂砾土对该涵洞地基进行换填处理达到地基承载力设计值。通过对地基换填后的涵洞基底土压力进行现场监测，可得不同填土高度(以涵洞基础底面为基准)下各测点的基底土压力与地基承载力设计值及本文公式得出的地基承载力对比曲线，如图11。

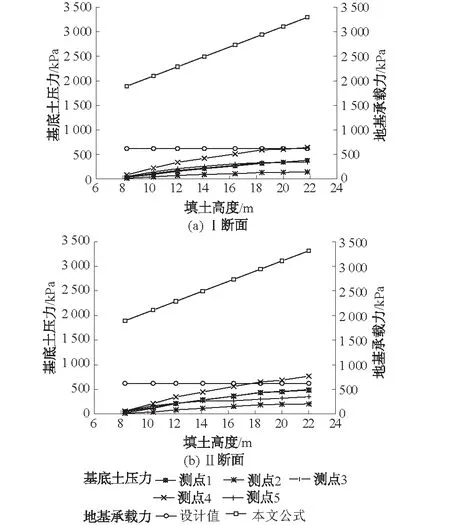
图11 Ⅰ断面、Ⅱ断面基底土压力及地基承载力对比曲线Fig.11 Curves of base soil pressure and bearing capacity of foundation of section Ⅰ and section Ⅱ

从图11可以看出，Ⅰ断面、Ⅱ断面基底土压力随填土高度的增加非线性增大，其增长趋势逐渐趋于平稳。当Ⅰ断面、Ⅱ断面填土高度分别达到21.8 m和18.4 m后，测点4的土压力均大于地基承载力设计值620 kPa，但现场涵洞地基并未发生失稳或强度破坏，原因在于现场确定涵洞地基承载力是在未建造涵洞之前对地基进行试验，由于未考虑基础埋深效应而低估了涵洞地基承载力。本文公式考虑了基础埋深效应，得出的地基承载力远远大于涵洞基底土压力，其最大值可达3 316 kPa，符合现场涵洞地基处于安全状态的实际情况。

6 结 论

(1)涵侧填土产生旁压荷载限制土体剪切破坏，增强了地基土的抗剪强度，使涵洞地基承载力得到提高，但地基承载力提高率逐渐降低。

(2)通过有限元软件分析可得，涵顶和基底土压力随距涵顶中线距离的变化呈“马鞍形”分布。随着填土高度的增加，涵洞台背填土受到附加土压力的影响增大。基底外填土所受土压力均小于上覆土自重γH，说明在地基承载力计算中应考虑台背填土所受的附加土压力对地基承载力的影响。

(3)随着地基土的内摩擦角和黏聚力的增加，地基承载力容许值分别呈非线性和近似线性增长趋势，且内摩擦角对地基承载力的影响程度明显大于黏聚力。

(4)通过将有限元计算值与普朗特尔公式、太沙基公式和本文公式计算所得的地基承载力容许值进行对比分析可得，本文公式计算值与有限元计算值符合较好。

(5)通过现场涵洞工程实例分析可得，涵洞地基承载力设计值由于未考虑基础埋深效应低估了涵洞地基承载力，本文公式得出的地基承载力值远远大于涵洞基底土压力，符合现场涵洞地基处于安全状态的实际情况。