大样本数据模型方法在中小河流流量测验中的应用

(1.长江科学院 科研计划处，武汉 430010； 2.襄阳市水文水资源勘测局，湖北 襄阳 441003； 3.湖北省水文水资源应急监测中心， 武汉 430070)

1 研究背景

近些年，受气候变化等环境因素影响，我国中小河流洪水灾害十分严重[1-2]。2011年以来，国家启动中小河流水文监测系统建设[3-4]，新建了大量的水文站点。新建站点在进行流量测验、建立水位-流量关系曲线时，基本都面临着数据匮乏的问题[3,5-7]。

传统的流量测验方法主要有流速仪法、浮标测流法、指标流速法、比降面积法等[8-9]。流速仪法是目前最常用的一种基础流量测验方法，主要通过流速仪测量断面特定位置的垂线流速，分块计算部分流量，最后叠加得到断面流量[10-11]。此方法需要建设配套的缆道设施，资金投入量大，测量过程耗时长，在没有缆道设施的地方，汛期或者发生洪水的时候，为了保障安全，工作人员无法在河面上开展流量测验工作[12-14]。浮标法是一种简单的流量测验方法，容易受测验人员和河道漂浮物的影响，精度较差[15-19]。指标流速法是目前一种比较新的测验方法，主要选取断面某一代表性区域的流速来拟合断面流量，主要借助H-ADCP(水平声学多普勒流速剖面仪)等设备进行测量，同时也存在资金投入量大、指标流速选择困难等问题[20-21]。比降面积法经济、简便，需要对主要参数糙率做全面系统的分析[22-23]，但是新建站点无历史测验资料，同时由于糙率不太稳定、比降测量精度受限等原因，比降面积法存在精度不高的问题[24-25]。综上所述，目前工程实践需要解决传统流量测验方法中成本高、测量过程耗时耗力的问题。

经过在工程项目中的不断探索，将传统断面流量计算理论和最新表面流速测验技术相结合，本文实现了一种基于大样本表面流速和断面水位数据输入来确立河道断面水位-流量关系曲线的方法。该方法对比测数据量要求低，方法简单，成本低，可显著提高精度。本文以石花水文站流量测验为例，探讨了基于大样本表面流速和断面水位数据输入实现河道断面流量测验的方法。

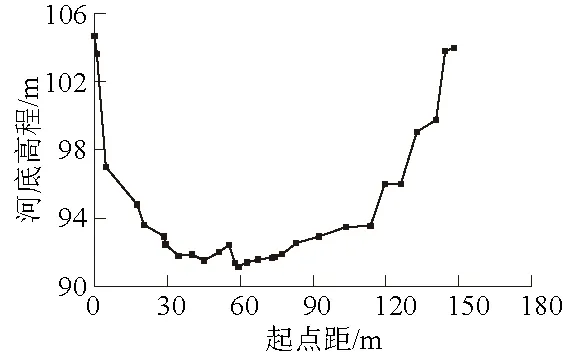
图1 石花水文站流量测验断面 实测高程Fig.1 Elevation of a flow measurement section at Shihua hydrological station

2 站点概况

石花水文站(东经111°27′44″，北纬32°16′39″)位于湖北省襄阳市谷城县石花镇余家店村,位于汉江中游水系，是汉江一级支流北河的控制站，流域面积1 070 km2。该站测验河段顺直长约600 m，常年水面宽60 m，河道两岸无河堤，水流畅通，河床由岩石组成，相对较稳定，流量测验断面高程如图1所示。经调查该站历史最高水位101.52 m，最低水位92.56 m，水位变幅8.96 m。在断面“0”起点距59.29 m和74.13 m处分别安装奥地利Sommer公司的RG-30表面流速测量探头1和探头2测量河道表面流速。

3 大样本数据流量测验模型

大样本数据流量测验模型，是基于表面流速、断面水位的大样本数据输入从而得到河道断面流量的测验方法。在模型参数率定的过程中，在给定模型参数初始值后，先通过选取实测流量时间附近的样本数据代入模型计算流量；然后以人工实测流量数据的相对偏差为优化目标函数，通过循环迭代方法修正模型参数，得到一组初定的最优解为模型参数；最后将表面流速和断面水位的大样本数据以及优化的分段糙率作为模型输入，计算出流量，通过计算的大样本流量数据拟合出水位-流量关系曲线。

3.1 大样本数据流量测验模型原理介绍

本模型以曼宁公式[26-29]为基础，在河道断面寻求垂线流速与断面平均流速的关系。模型以1～2条实测垂线流速为已知条件，反求能坡(水流能量坡度)参数，代替曼宁公式中比降与糙率的比值关系，建立与曼宁公式具有相同结构形式的垂线流速公式。其中，分段垂线条数一般不少于15条(15～20条)。河道断面分段垂线划分示意图如图2所示。

图2 河道断面分段垂线划分示意图Fig.2 Partition of a river section by segmented verticals

图2中，b表示垂线间距(m)；Rn(n=1,2,3,…)表示第n段水力半径(m)；Rt1，Rt2为探头所在位置的水力半径(m)。

根据探头所在位置的实测流速vt1，vt2和对河道分段糙率预估后探头位置对应的糙率nt1，nt2，先求出2个探头处比降St1和St2,即

(1)

(3)

(4)

式中k为河道断面形状修正系数。

表1 河道断面水位、流量、流速实测数据Table 1 Observations of water level, flow rate, and flow velocity at the river section

表2 人工实测流量和模型计算流量对比分析Table 2 Comparison of flow rate between manual measurement and model calculation

3.2 大样本数据流量测验模型参数率定

根据实测的表面流速、水位数据，结合已知的断面资料，代入预估的河道分段糙率和河道断面形状修正系数k的初始值(一般设定为1)，然后可通过实测流量和模型计算流量的比值范围选定一个修正系数基值，再迭代修正。通过3.1节所述模型计算断面流量，以人工实测流量数据为标准(人工实测流量数据要剔除不合理的测量数据)，若模型计算得到的流量数据相对偏差超出可接受偏差范围(本文采用±5%以内)，则调整河道断面糙率和河道断面形状修正系数k，重新代入模型中计算得到断面流量,然后再次计算模型模拟偏差并判断是否在可接受偏差范围内。当模型模拟断面流量的偏差满足可接受偏差范围，此时对应的河道断面分段糙率和河道断面形状修正系数k是合理的，为最终的模型参数率定值。基于率定好的模型，将大样本的实测流速、水位数据作为模型输入，驱动模型得到断面流量模型模拟输出数据。通过模型计算的流量，结合对应的水位数据，拟合出该断面的水位-流量关系曲线。具体流程如图3所示。

图3 大样本数据流量测验模型参数率定流程Fig.3 Flowchart of parameter calibration for the large sample input model for flow measurement

3.3 大样本数据流量测验模型率定结果

根据石花站水文特性，河道断面糙率的经验初始值为：起点距0～50 m选0.031，50～100 m选0.028，100 m以后选0.031；河段断面形状修正系数的初始值取1。为了减少RG-30探头采集的流速误差，选取人工实测流量时间段以及前后几次的平均流速作为有效数据，同时结合河道断面糙率和形状修正系数的初始值，代入模型计算流量，然后计算模型模拟流量相对于人工实测流量的相对偏差。以相对偏差为模型参数率定的优化目标函数，以±0.001为步长，逐步率定河道断面糙率和形状修正系数。河道断面水位、流量、流速实测数据如表1所示，人工实测流量和模型计算流量对比分析如表2所示。

根据相对偏差计算，6个测次相对偏差结果均在5%以内，说明所取得的河道断面分段糙率和形状修正系数k值合理，可以认定是一组合理的模型参数。表2结果最终选择的河道断面分段糙率是：起点距0～50 m选0.032，50～100 m选0.028，100 m以后选0.032；河道断面修正系数k值取0.542 3。

4 水位-流量关系分析

基于3.3节模型参数率定结果，选择输入数据驱动模型。2016年8月8日，石花站点有次涨落水过程，水位变幅5 m左右。选取2016-08-08T10:15—2016-08-09T 23:55这段时间388组有效的断面水位、探头1和探头2流速数据作为大样本数据，输入模型，得到模型模拟的断面流量。根据断面水位数据、模型模拟的断面流量和人工测量的断面流量，绘制石花站的水位-流量数据散点图，如图4中的模型计算流量和人工实测流量散点所示。

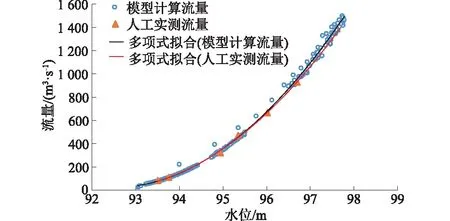
图4 模型模拟和人工实测水位-流量关系曲线Fig.4 Stage-discharge curves based on model simulation and manual observation

通过分析一个回合涨水-落水水位-流量数据散点图可知，石花站点的水位-流量关系是单调曲线。采用2阶多项式，分别拟合模型模拟的水位-流量散点数据和人工实测下的水位-流量散点数据，得到对应的水位-流量关系曲线，如图4中的多项式拟合曲线所示。

根据模型模拟的水位-流量散点数据，得到石花站点水位-流量关系曲线的高精度多项式，即

y=51.903 092 764 568 3x2-

9 597.018 707 632 67x+443 649.292 279 402 。

式中：x为水位(m)；y为流量(m3/s)。

选取2018年4月1日—8月7日的断面水位和表面流速数据，其中删除掉流速为0以及其他情况的无效数据，共11 450条数据。此时间段水位变幅2 m左右。对站点水位、表面流速和模型模拟流量过程线进行趋势分析，如图5所示。3类水文变量(水位、流速、流量)趋势一致，中间只有零星突变情况。从图5(b)流量过程线可以看出，流速突变造成的误差不是太大。这说明河道水位-流量关系正常，建立的模型和参数的选择比较合理。

图5 实测流速、实测水位和模型模拟流量过程线Fig.5 Curves of observed velocity and water level and model simulated flow rate

5 结 语

本文以中小河流建设项目为背景，提出一个以大样本的表面流速和断面水位数据为输入的模型方法，用于计算河道的断面流量。

该方法通过少量实测中高水位流量数据率定河段断面分段糙率和形状修正系数，将大样本的表面流速和断面水位数据作为模型输入，从而通过率定好的模型计算河段断面流量，可以满足中小河流水文站报汛的精度要求。

在该方法中，表面流速测量容易受到风、河道表面漂浮物等影响，实测流速偶尔出现突变值。这些突变值可以在后续数据入库时处理掉。该方法的适用性需要基于一定限制假设，由于是根据测量河道某一点或几点的表面流速计算河道断面流量，该方法对河道自身特性有一定要求，河道需较规则，如呈现抛物线型、矩形等，同时上下游无挡水建筑物。对于冲淤变化较大的断面，应加测断面测量，并根据变化情况调整部分糙率和形状修正系数，一般天然河道比较容易具备该方法的适用条件。

传统方法中，人工测量流量是一个持续时间段过程，这个期间河道水位会出现变化，模型计算是一个瞬时计算过程，两者之间会出现少量不可避免的误差,而大样本数据的拟合分析是比较合理的减少误差的手段。综上所述，本文提出的方法优势在于能快速分析河道水位-流量关系特性，拟合水位-流量关系曲线，减少了传统方法拟合水位-流量关系曲线需测量流量的次数，从而减少误差、提高精度、降低了时间和经济成本。