斜向进水消力井淹没射流水力特性机理分析

(云南农业大学 水利学院，昆明 650201)

1 研究背景

斜向进水消力井作为一种新型消能工，工程结构简单，消能效率好，地形适应性强，在山区峡谷型水库中是一种相对合理、可行的选择[1]。

消力井的概念最早由郭子中[2]提出，而后国内外专家学者分别对消力井进行了广泛而深入的研究，其中多以深筒式或旋流式竖向进水消力井为主,这些理论研究很大程度上深化了人们对于消力井的认识，对实际工程的建设应用也起到了一定的推动作用。近年来，金瑾等[3]通过水工模型试验对直径变化下竖井溢洪道各个重要部分的特征压强作了研究，试验得到在不同直径下消力井各部分压强特征参数的沿程变化趋势。衡海龙等[4]运用理论分析探讨了影响改进型深筒式消力井流量系数的主要因素与流量之间的定量关系，建立了改进型深筒式消力井过流能力计算方程。孙高升[5]利用水工模型试验得到了消能效率及井底压强在方形消力井内的变化规律。南洪等[6]通过对竖井溢洪道结构及参数设计研究，较好地解决了峡谷河道工程布置及施工干扰问题。冯博等[7]结合工程实例原型对深筒式消力井消能效果进行了较为系统的水力学模型试验验证。

由于消力井井内水流流态复杂，既有成果多针对竖向进水水工模型试验或实际工程进行水力特性研究。相对而言，斜向进水消力井研究成果较少，文献[1]通过水工模型试验对消力井内的内部水流流态进行了初探，但尚未对其水力特性机理做进一步研究。

本文通过理论分析与水力学试验，对斜向进水消力井内的淹没射流扩散衰减规律及冲击射流力机理进行研究，以期揭示射流沿程最大流速及水股作用力的变化特性。

图1 斜向进水消力井 水流结构Fig.1 Flow structure in dissipation well with inclined intake

2 射流机理分析

2.1 紊动射流分区

大量试验发现，斜向进水消力井内的典型水体特征为斜向淹没冲击射流与淹没水跃流的复合流态。入井射流水股沿轴线方向可分为3个区域(图1)，即射流淹没区(Ⅰ)、射流冲击区(Ⅱ)和附壁漩流区(Ⅲ)。其中在射流淹没区，主流运动规律与平面自由紊动射流接近，满足动力自相似条件；在射流冲击区，主流受到井壁冲折转向，动水压强随流速骤减而急剧增大，井壁结构可能在巨大作用力下形成失稳破坏，表现出明显的冲击射流特征；但在附壁旋流区，主流沿上下缘紊动扩散并跃起，断面流速梯度分布不均，下壁面动水压强较大并形成表面水突旋滚，淹没水跃特征明显[8-9]。

2.2 射流沿程最大流速衰变规律

如图2所示，沿射流主流线建立直角(xOy)坐标系：泄槽出口面与射流主流轴线交点为坐标系原点O,沿淹没射流主流方向(轴向)设为x轴，与淹没射流主流垂直方向(垂向)设为y轴。

注：v1为泄槽流速；h0为入池水深；h为淹没深度；H为跌坎深度；θ为泄槽纵坡角；θ1为射流夹角；θ2为射流扩散角；b为射流半扩散宽度;umax为射流沿程各断面轴向最大流速；Pmax为与主流线垂直断面上轴心处动水压强。图2 斜向进水消力井水流扩散示意图Fig.2 Schematic diagram of water flow diffusion in dissipation well with inclined intake

根据淹没射流基本特征，得到简化定常流Reynolds方程组。取射流沿程各断面轴向最大时均流速umax和射流半扩散宽度b0.5umax为射流速度场的特征尺度[2]，根据相似性条件，可设各断面纵向时均流速分布函数关系为：

式中：u为时均流速；τ为切应力；ρ为密度；η1为相似变量；y为断面时均流速u=0.5umax对应的射流半扩散距离。

(2)

式中：u0为泄槽末端水流断面平均流速；x为距入井断面的距离；h0为泄槽入池水深；m为幂指数。

斜向进水条件下，消力井淹没射流运动近似符合平面直线扩散规律，关于射流轴线对称的各断面流速是相似或自保持的高斯分布[11]，对淹没射流入井断面动量P1沿程积分，并令斜向淹没射流到达冲击点时的动量P2=nP1，考虑底板及边壁的约束作用，需增加一常数C0[11]，整理可得简化射流沿程最大速度表达式为

(3)

式中λ，n为待定系数。

2.3 射流沿程压强分布特性

将二维冲击射流作用于接触面上的时均压强进行量纲和谐处理，无论是垂直射流还是倾斜射流，其试验点均聚集在一起，存在很好的相似性，可以表示成正态分布曲线[10]，即

P/Pmax=exp(kη22) 。

(4)

式中：P为任意点的动水压强；Pmax为与主流线垂直断面上轴心处的动水压强；k为待定系数；η2为任意测点与最大时均压强点之间的距离y与压强分布半值宽度b0.5P的比值，是相似变量。

对于自由射流，它内部压强和周围流体是相同的，不存在压力梯度[12]。由能量守恒定律，根据式(4)可得斜向进水条件下消力井内冲击区上任意一点的动水压强分布式为

(5)

图3 坐标系平移和旋转Fig.3 Translation and rotation of coordinate system

2.4 沿射流方向水股作用力

如图3所示，x，y，z是泄槽末端上建立的坐标系，坐标原点O与射流源点重合，x轴沿射流主流线方向。X，Y，Z是井壁曲面上建立的坐标系，坐标原点O与井壁中线重合，X轴沿井壁中轴线方向，构造变换矩阵使两坐标系平移旋转重叠，其中θ为水流的入池角度。

由xyz坐标系相对于XYZ坐标系的单位坐标向量分别构造关于坐标原点的平移矩阵I和旋转矩阵R,得到坐标系XYZ到xyz的坐标变换矩阵为I(-X0,-Y0,-Z0)R，由坐标变换可分别得到X，Y,Z的取值范围为

(6)

假设A为冲击区宽度，斜向进水消力井两端为井壁，即η是有限的，则冲击区的范围为-2.4≤η≤2.4，同时当η≤-2.4或者η≥2.4时，P值无限趋近于0[13-14]。对式(5)给出的压强分布，对井壁冲击区进行积分(Z=0)，得到斜向进水消力井井壁时均作用力F时(方向垂直井壁)的积分公式为

(7)

式中：L为旋滚区长度；LC为冲击区长度；θ为入射角度。

3 射流沿程最大流速及作用力分析

如前所述，利用机理分析建立的表达式，结合边界条件，即通过水力学试验研究进行一定纵坡下的参数(n，D，E)率定。

模型材料为有机玻璃，采用正态模型，按照重力相似准则设计。流量采用三角堰施测，水位采用精度0.1 mm的测针施测，流速采用OA型直读式多功能测速仪测定，压力通过脉动压力传感器测定。

井筒为内径0.58 m的圆形，由底坡i=1∶1.5、宽度0.15 m的泄槽斜向进水，出口为坡度i=0 、宽度0.25 m且与泄槽轴线正交的尾水渠，底板高程与泄槽末端高程0.40 m一致(图4)。

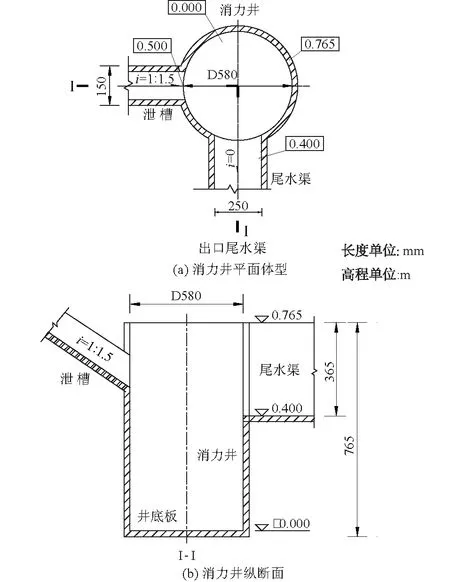
图4 斜向进水消力井体型示意图Fig.4 Schematic diagram of dissipation well with inclined inlet

3.1 最大流速及冲击区井壁时均作用力

在射流区，与射流正交各断面最大流速点(umax)位置的连线为主流线，主流线位置如图5所示。忽略射流较短初始段对主流线位置的影响，将射流主流线简化为直线，利用Origin软件拟合分析得到主流线位置分布(相关系数R2=0.988 1)，即

y=-0.874 04x+29.761 2 。

(8)

图5 射流区主流线位置Fig.5 Main streamline location in the jet stream area

当消力井的入井流量Q分别为8,12,16 L/s时，一定纵坡下斜向进水消力井射流沿程最大流速的试验成果见表1。

表1 斜向进水条件下射流沿程最大流速试验成果Table 1 Experimental results of the maximum velocity of the mainstream axial flow under oblique inlet condition

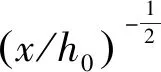
图6斜向进水条件下射流轴向最大速度Fig.6 Maximum velocity of axial flow under oblique inlet condition

经拟合分析得到斜向进水条件下，主流线在主体段上的射流沿程最大流速公式，即

R2=0.933 35 。

(9)

在式(7)中，令：

(10)

将式(9)、式(10)代入式(7)得到井壁时均冲击力F时表达式,即

63.27D-27.14E) 。

(11)

其中：

3.2 机理分析成果验证

式(9)、式(11)分别给出了计算斜向进水条件下射流沿程最大流速和冲击区井壁时均作用力的半经验公式，可以据此计算射流沿程最大流速和冲击区井壁时均冲击力。

将流量Q=6 L/s和Q=18 L/s时的半经验公式计算结果和有限水域物理试验实测的射流沿程最大流速(采用测速仪垂直射流方向测试得到)、冲击区井壁时均作用力进行对比，如表2、表3。

根据表2，流量为6 L/s时的射流沿程最大流速计算值和实测值绝对误差范围在0.01～2.68 m/s之间，18 L/s时的绝对误差范围在-0.04～-1.21 m/s之间，而且6 L/s情况下的相对误差较之18 L/s大；此外，不管流量大小，射流初始段计算值均较大。原因在于机理分析时，将射流初始段周围视为自由空间，未考虑消力井内淹没水深对流速的衰减作用；也未考虑消力井内水体对小流量射流水股的弹射作用。由表3可知，井壁处的射流冲击力试验值与计算值基本吻合。

表3 冲击区井壁作用力对比分析Table 3 Comparison and analysis of the impact force of the shaft wall

4 结 语

结合斜向进水条件下消力井内水流流态特征，依托有限水域物理模型试验研究成果，推求出一定泄槽纵坡斜向进水条件下消力井射流沿程最大流速分布半经验计算公式，进而得出消力井冲击区井壁时均作用力的计算公式。经验证，公式计算结果和试验研究成果吻合良好，能够满足工程设计要求。